Мы делаем систему симуляции различных процессов, в которой пользователь с помощью визуального программирования может описать и посмотреть, как работает тот или иной процесс. Иными словами, проверить, как на результат процесса влияют те или иные причинно-следственные связи. Вся система построена на нодах - наглядных представлениях функций, которые принимают, обрабатывают, показывают и в конце концов отправляют данные в следующие ноды.
Рубрика «кривые безье»
Как рисовать красивые соединения с помощью SVG
2023-03-03 в 15:32, admin, рубрики: html, html-верстка, javascript, svg, веб-дизайн, векторная графика, кривые безье, Программирование, Работа с векторной графикой, соединенияМатематика самонаводящихся ракет из аниме
2023-02-23 в 6:34, admin, рубрики: unity, Алгоритмы, кривые безье, математика, разработка игр, ракеты, симплекс-шум, шум перлина
Я создал прототип ракетной атаки! Для этого понадобилась хитрая математика, о которой будет рассказано в этой статье.
Мы поговорим о кубических кривых Безье, шуме Перлина и rotation minimizing frames.
Читать полностью »
Кривые Безье. Немного о пересечениях и как можно проще
2020-10-11 в 12:45, admin, рубрики: c++, Алгоритмы, кривые безье, математика, полиномы бернштейна, рекурсивный алгоритмArticle
Вы сталкивались когда-нибудь с построением (непрерывного) пути обхода кривой на плоскости, заданной отрезками и кривыми Безье?
Вроде бы не сильно сложная задача: состыковать отрезки кривых в один путь и обойти его "не отрывая пера". Замкнутая кривая обходится в одном направлении, ответвления — в прямом и обратном, начало и конец в одном узле.
Всё было хорошо, пока из-под рук дизайнеров не стали вылезать монструозные пути, где отдельные кривые могли пересекаться или не точно состыковываться. Объяснение было предельно простым — визуально они все лежат как надо, а для станка, который этот путь будет обходить, такие отклонения незаметны.
Вооружившись знанием о величине максимально допустимого отклонения, я приступил к исследованию, результатами которого хочу поделиться.
Адаптивное разбиение кривых Безье 2-го и 3-го порядка
2020-06-14 в 19:39, admin, рубрики: python, аппроксимация, векторная графика, кривые безье, Программирование, Работа с векторной графикой
Уже год как я сменил работу на новую. В этой статье я хочу поделиться опытом, накопленным на прошлом месте. Здесь рассмотрены методы аппроксимации кривых Безье, а также обработка исключительных случаев, при которых простые алгоритмы показывают себя не очень хорошо. Все, кому близка тема векторной графики — прошу под кат.
Почему векторная графика 2D намного сложнее, чем 3D
2019-05-12 в 9:48, admin, рубрики: Oculus Medium, postscript, sdf, signed distance fields, tex, кривые безье, неявные кривые, неявные поверхности, обработка изображений, поля расстояний со знаком, Работа с векторной графикой, типографикаВ последнее время появилось много фантастических исследований по 2D-рендерингу. Пётр Кобаличек и Фабиан Айзерман работают над Blend2D: это один из самых быстрых и точных CPU-растеризаторов на рынке, с инновационной техникой JIT. Патрик Уолтон из Mozilla изучил не один, а три разных подхода в Pathfinder, кульминацией чего стал Pathfinder v3. Раф Левиен построил вычислительный конвейер по технологии, описанной в научной статье Гана с коллегами о векторных текстурах (2014). Похоже, некое дальнейшее развитие получают поля расстояний со знаком: здесь независимо работают Адам Симмонс и Сара Фрискен.
Кто-то может спросить: а почему вокруг 2D так много шума? Это ведь не может быть намного сложнее, чем 3D, верно? 3D — совершенно другое измерение! Тут у нас на носу трассировка лучей в режиме реального времени с точным освещением, а вы не можете осилить невзрачную 2D-графику со сплошными цветами?
Для тех, кто не очень хорошо разбирается в деталях современного GPU, это вправду очень удивительно! Но в 2D-графике множество уникальных ограничений, которые чрезвычайно её усложняют. К тому же она не поддаётся параллелизации. Давайте прогуляемся по исторической дорожке, которая нас сюда привела.
Читать полностью »
Отчаянный поиск квадрокруга
2018-04-09 в 7:46, admin, рубрики: apple, iOS 7, генетический алгоритм, графический дизайн, дизайн интерфейсов, дифференциальная геометрия, квадрокруг, клотоиды, кривизна, кривые безье, математика, ограничения дизайна иконки, плоские кривые, промышленный дизайн, Работа с векторной графикой, разложение в ряд, разработка под iOS, степенные ряды, суперэллипс, Чарльз ИмзПоиск таинственной математики, на которой основана фигура в iOS

Это история о том, как один инженер Figma искал идеальный ответ на программистскую задачу.
В знаменитом интервью 1972 года Чарльз Имз кратко ответил на несколько фундаментальных вопросов о природе дизайна. Отвечая на первый вопрос, он определил дизайн как «план компоновки элементов для достижения определённой цели».
Остальные ответы тоже очень лаконичны, вплоть до метафор. Но когда Имза спросили о роли ограничений дизайна, он остановился и выдал самый длинный и самый продуманный ответ за всё интервью: «Один из немногих эффективных ключей к проблеме дизайна — это способность дизайнера распознавать как можно больше ограничений; его готовность и энтузиазм к работе в этих ограничениях».
Хотя я не дизайнер по профессии — я разработчик Figma, веб-инструмента совместного проектирования — несложно заметить, что замечания Имза относятся и к моей работе. Вместо элементов UI я выраженные в коде компоную математические концепции для создания инструментов и функций. И ограничения времени, простоты, поддержки и даже эстетики играют похожую доминирующую роль в моей работе.
Читать полностью »
Кривые Безье и Пикассо
2017-12-22 в 8:23, admin, рубрики: Алгоритмы, компьютерное искусство, кривые безье, математика
Пабло Пикассо в своей студии на фоне картины «Кухня», фотография Херберта Листа.
Художник и простота
Одни из самых любимых мной работ Пабло Пикассо — это его линейные рисунки. Он изобразил на некоторых из них животных: сову, верблюда, бабочку и т.д. Эта работа под названием «Собака» висит на моей стене:
(Можете перейти к интерактивному демо, в которой мы воссоздали «Собаку» с помощью представленных в статье математических расчётов)
Эти рисунки чрезвычайно просты, но каким-то образом им удаётся глубоко тронуть зрителя. Они создают впечатление простоты композиции и реализации. Одно движение руки и подпись создают настоящий шедевр! Рисунок одновременно кажется и небрежной импровизацией, и точно подобранной увертюрой в симфонии изящества.Читать полностью »
Кривые Безье-де Кастельжо. Canvas HTML5
2015-01-28 в 13:40, admin, рубрики: canvas, javascript, кривые безье 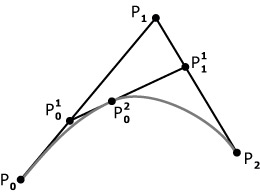
Предисловие
В свободное время решил заняться интересным делом. В голову пришла идея написать небольшой фреймворк для canvas (хоть и велосипед, но тоже интересно). Дело дошло до кривых Безье.
Решил как-то приукрасить встроенное решение, но у него есть один недостаток. Проблема в том, что функции квадратичной и кубической кривой выдают уже готовый результат, не подлежащий редактированию. Мне же требовалось обрисовывать кривую постепенно или обрисовать только часть кривой, не говоря уже о том, что хотелось обрисовывать кривые большего порядка, нежели 2-3 степени.
Читать полностью »
Построение волнистой линии через Кривые Безье
2014-08-11 в 14:54, admin, рубрики: .net, кривые безье, математикаДоброе время суток. Сегодня я хочу рассказать вам про рисование симметричной волнистой линии при помощи Кривых Безье, используя только 2 точки.
Предисловие
При создании CAD-систем, часто возникает необходимость рисования не просто прямых линий, а волнистых или ломаных. Так как в обоих случаях линия симметрична относительно прямой, проходящей через начальную и конечные точки, то необходимо вычислить точки, лежащие на параллельных главной прямых. О том, как это сделать, пойдет речь ниже.
Читать полностью »
Бесплатный редактор шрифтов на HTML5
2014-03-05 в 14:38, admin, рубрики: html, кривые безье, типографика, метки: кривые безьеВсё больше полезных программ удаётся портировать на открытые веб-технологии. До сих пор среди них не было редактора шрифтов. Теперь есть: Glyphr.
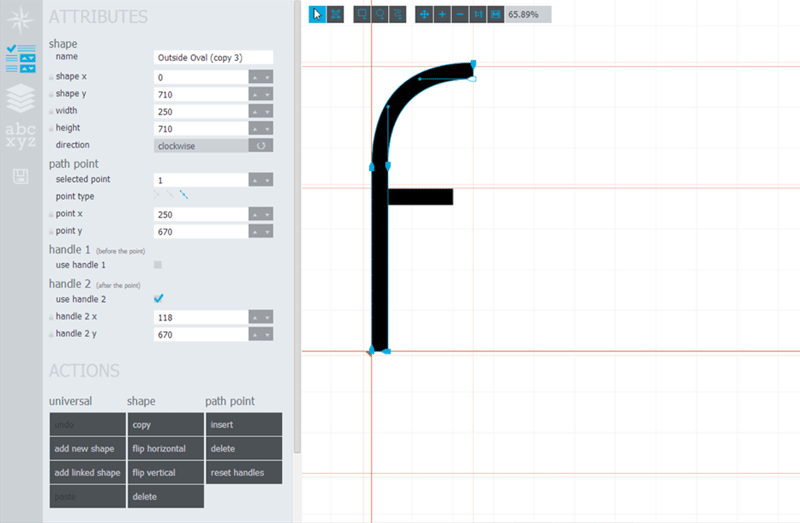
Профессиональный софт для проектирования шрифтов — это сложные и дорогие программы. В отличие от них, интерфейс Glyphr вполне доступен для каждого желающего, а само приложение совершенно бесплатно.
Читать полностью »
