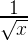В этой статье мы поговорим о «магической» константе 0x5f3759df, лежащей в основе элегантного алгоритмического трюка для быстрого вычисления обратного квадратного корня.
Вот полная реализация этого алгоритма:
float FastInvSqrt(float x) {
float xhalf = 0.5f * x;
int i = *(int*)&x; // представим биты float в виде целого числа
i = 0x5f3759df - (i >> 1); // какого черта здесь происходит ?
x = *(float*)&i;
x = x*(1.5f-(xhalf*x*x));
return x;
}Этот код вычисляет некоторое (достаточно неплохое) приближение для формулы
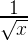
Сегодня данная реализация уже хорошо известна, и стала она такой после появления в коде игры Quake III Arena в 2005 году. Её создание когда-то приписывали Джону Кармаку, но выяснилось, что корни уходят намного дальше – к Ardent Computer, где в середине 80-ых её написал Грег Уолш. Конкретно та версия кода, которая показана выше (с забавными комментариями), действительно из кода Quake.
В этой статье мы попробуем разобраться с данным хаком, математически вывести эту самую константу и попробовать обобщить данный метод для вычисления произвольных степей от -1 до 1.
Да, понадобиться немного математики, но школьного курса будет более, чем достаточно.