В качестве КДПВ представлен математик Эварист Галуа, имя которого увековечено в обозначении конечных полей: GF (Galois field).
Вспомним что Галуа имел отношение, не только к конечным полям, но и к таким фундаментальным понятиям как: группа, поле и вообще считается основателем современной высшей алгебры.
Поделюсь с вами одной историей. Около двадцати лет назад я получил степень по физике, но занимался реверс-инжинирингом и криптоанализом. Наша компания AccessData работала в конце 90-х и начале 2000-х. Тогда правительство США постепенно снимало ограничения на экспорт криптографии, однако парольная защита в большинстве программ по-прежнему оставалась довольно бесполезной. Мы брали офисные программы, я проводил реверс-инжиниринг и выяснял алгоритм шифрования, а потом ломал криптозащиту.
Это был нескончаемый поток интересных, но не особенно сложных математических головоломок. За всё время я написал около сорока взломщиков паролей. Мы продавали их домашним пользователям, системным администраторам, местным и федеральным правоохранительным органам. Мне пришлось несколько раз съездить в федеральный центр подготовки сотрудников правоохранительных органов в Глинко, чтобы объяснить ребятам из Секретной службы, ФБР и АТФ основы криптографии и как использовать наши продукты.
Особенно ярко мне запомнились два проекта. Первым был Microsoft Word 97. До его появления файлы шифровались с помощью XOR байтов открытого текста и 16-байтовой строки, которая выводилась из пароля. Самыми распространёнными байтами в файле Word обычно были 0x00, 0xFF или 0x20 (пробел), поэтому мы просто выбирали самый распространённый символ в каждом столбце и проверяли 316 вариантов. Восстановление ключа обычно происходило мгновенно, но чтобы людям не казалось, что они зря потратили деньги, мы вставили небольшую анимацию, похожую на голливудскую хакерскую сцену с множеством случайных символов, из которых постепенно проявляется правильный пароль.
Читать полностью »
Многие помнят публикацию о «Рэйдикс» на Хабре «Как разработчики сидели в Петербурге и тихо ели грибы», в которой партнеры кратко изложили историю появления нашего продукта. Поэтому в первой статье своего Хаброблога мы бы хотели погрузиться в математические основы технологий RAIDIX.
В этой статье будет рассмотрена тема построения и работы с конечными полями (или полями Галуа), которые используются в криптографии, теории информации и кодирования и других науках, т.е. имеют широкое практическое применение.
Сухую теорию о группах/кольцах/полях можно прочитать по ссылке Поля Галуа, а здесь будет больше практики и реализации на языке Scala.
Для начала следует обсудить технические проблемы связанные с представлением полиномов в памяти, с учетом размеров типа Int в языке Scala. Требования сформулированы в списке ниже.
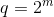элементовСначала опишем класс Polynomial, который реализует полином и 4 операции.
Этот вид полинома является «полуфабрикатом» и не привязан к конечному полю.
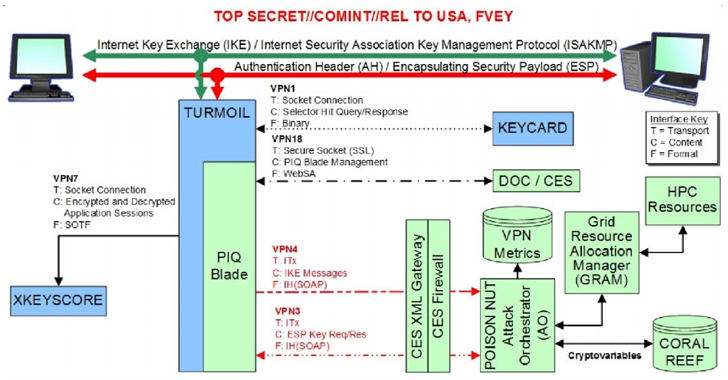
Слайд из презентации АНБ
В 2013 году благодаря Эдварду Сноудену в СМИ попали документы АНБ. Среди них — замыленный слайд из презентации, который указывал на возможности АНБ по расшифровке трафика VPN. У АНБ не было причин врать в засекреченной презентации, так что специалисты восприняли эту информацию как свидетельство наличия некоей фундаментальной уязвимости в современных системах криптографии с открытым ключом.
Читать полностью »
