Создание продуктов на основе якорных инвестиций – важный этап для любой компании, независимо от ее сферы деятельности. Нужна хорошая подготовка с акцентом на профессиональную презентацию как продукта, так и услуги. Физический товар можно увидеть и протестировать, но как быть с программным обеспечением, лишенным физических свойствами? Как убедить инвестировать в нечто виртуальное?
Рубрика «изометрия»
2D-ролик: как вложиться не в эфир, а в результат
2024-11-28 в 7:15, admin, рубрики: 2D ролик, 2D-анимация, изометрия, роликТренды дизайна в 2018: прогноз и реальность
2018-08-10 в 8:51, admin, рубрики: 3d, AR, анимация, Блог компании FunCorp, веб-дизайн, веб-сайты, графический дизайн, дизайн, дополненная реальность, изометрия, каллиграфия, Разработка веб-сайтов, типографика, тренды 2018, тренды дизайна, фотография
Примечание переводчика: эту замечательную статью не перевели для Хабра ни в начале года, ни позднее. При том что она действительно полезная и заслуживает внимания. Поэтому, несмотря на то, что почти ⅔ 18-го года уже прожиты, я всё-таки решилась на перевод. Заодно сравнила прогнозы с реальностью, о чём оставила комментарии по тексту.
Внимание: под катом много тяжёлых гифок и красоты!
Читать полностью »
Теорема Бошерницана
2018-07-15 в 8:34, admin, рубрики: Блог компании Trinity Digital & Баласс Group, Занимательные задачки, изометрия, компакт, математика, метрическое пространство, расстояние, репетитор математика, теорема, теорема бошерницанаВ статье дано простое доказательство того, что отображение компактного метрического пространства в себя, не уменьшающее расстояния, является изометрией.
Отображение
метрического пространства с метрикой 
называют изометрией, если для любых 
справедливо равенство 
. Мы докажем здесь следующее утверждение:
Теорема. Если
отображение компактного метрического пространства в себя, такое что
для любых
, то отображение
— изометрия.
Напомним некоторые простые утверждения о метрических компактах и введём некоторые соглашения и определения, необходимые для дальнейшего изложения.
Через 
будем обозначать количество элементов конечного множества 
.
Для 
и 
множество 
назовем 
-окрестностью точки 
(или открытым шаром с центром в точке 
и радиусом 
).
Конечное множество 
назовём 
-сетью в 
(или просто 
-сетью), если для любой точки 
найдётся точка 
такая, что 
. Множество 
назовём 
-разреженным, если 
для любых 
, таких, что 
.
Для любого конечного множества 
обозначим через 
сумму 
. Величину 
назовём длиной множества 
.
Читать полностью »
Изометрия, z-индексы в мобильных играх и их оптимизация
2018-06-25 в 5:11, admin, рубрики: Gamedev, iOS, objective-c, spritekit, swift, xcode, z-index, изометрия, разработка мобильных приложений, я пиарюсь
Привет! Недавно мы вышли в релиз с нашей игрой, которую долго и упорно готовили и в процессе которой накопилось немалое количество интересных тем, которыми стоит поделиться с сообществом. Тема будет интересна далеко не только iOS и иным мобильным разработчикам, но и всем тем, кому интересно, как всякие графические вещи работают под капотом, а также всем фанатам 2D-стратегий, коим уже третее десятилетие являюсь я сам.
Читать полностью »
Как создаются изометрические миры
2017-07-13 в 7:39, admin, рубрики: html5, phaser.js, изометрические игры, изометрия, разработка игр, метки: изометрические игры, изометрия
Все мы играли в потрясающие изометрические игры, будь то первые Diablo, Age of Empires или Commandos. При первой встрече с изометрической игрой можно задаться вопросом: двухмерная она, трёхмерная или нечто совершенно другое. Сам мир изометрических игр обладает волшебной притягательностью для разработчиков. Давайте попробуем раскрыть тайну изометрической проекции и создадим простой изометрический уровень.
Для этого я решил использовать Phaser с кодом на JS. В результате у нас получится интерактивное приложение HTML5.
Учтите, что это не туториал по разработке на Phaser, мы просто используем его для удобного ознакомления с базовыми концепциями создания изометрической сцены. Кроме того, в Phaser есть простые способы создания изометрического контента, например, Phaser Isometric Plugin.
Для упрощения при создании сцены мы будем использовать тайлы.
Читать полностью »
Сложности при создании изометрической игры в Unity
2017-03-20 в 10:02, admin, рубрики: unity3d, двухмерная игра, изометрия, разработка игрДля начала небольшое предисловие. Мы работаем над игрой Empires in Ruins с пререндеренными 3D-моделями, которые перед сохранением в Unity превращаются в спрайты и атласы спрайтов. Если объяснять коротко, то при этом выполняется довольно долгий и медленный производственный процесс, но он позволяет нам использовать текстуры очень высокого разрешения для очень чёткой графики. Такой стиль напоминает стратегические игры 90-х наподобие Age of Empires (и многих других) в смеси с производственным процессом Baldur's gate, дополненным современным стилем и возможностью сильного масштабирования. Нам вообще нравится производить впечатление.
Должен сказать, что мы пока абсолютно довольны результатами, и людям в Интернете они тоже нравятся, но мы скорее согласимся на пытки, чем начнём делать ещё одну игру в том же стиле.
Причины просты: результаты может быть и замечательны, но на самом деле трудно найти более медленный рабочий процесс. Для самой первой игры это вполне нормально, работа продолжается бесконечно, и мы наслаждаемся процессом, урок усвоен. Но в будущем стоит всё же выпускать одну игру чаще, чем раз в пять лет.
Читать полностью »
Техника тотального предрасчёта в алгоритме освещения для тайловой 2D игры
2016-11-23 в 15:16, admin, рубрики: 2d, Action Script, air, Алгоритмы, игры, изометрия, разработка игрПривет! Моя последняя игра – изометрическая бродилка, одной из особенностью которой является «исследование» территории: изначально карта чёрная и игрок открывает этот «туман войны» по ходу игры. Причём видимость тайлов зависит не только от расстояния до персонажа, но и от окружения: клетки за непрозрачными стенами не видны, даже если подойти в упор, а, например, кустарник ухудшает видимость клеток за ним на 50%.
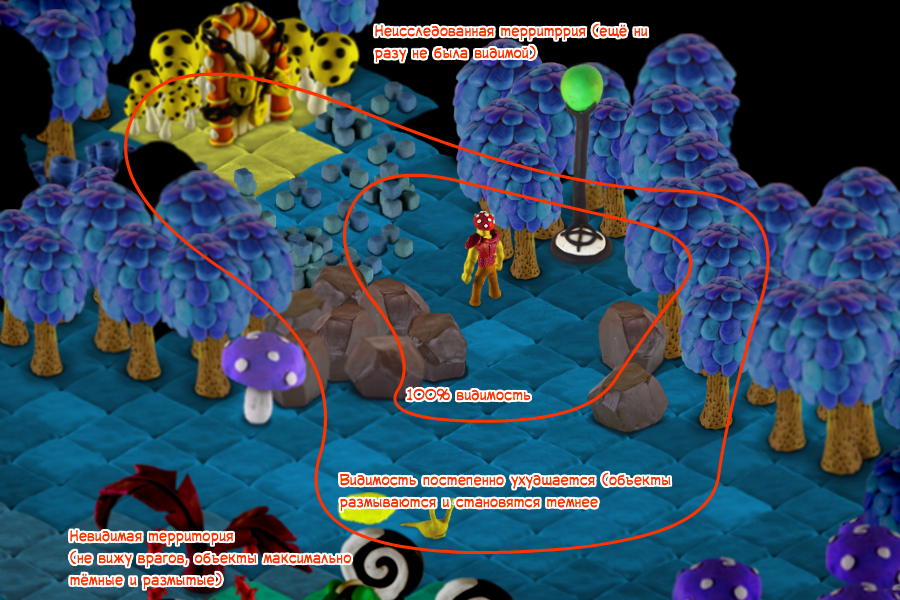
Чтобы не нагружать процессор покадровой трассировкой лучей (для определения какая клетка насколько в данный момент «видима»), я использовал довольно интересный метод «тотального предрасчёта» – основные параметры для фактически всех возможных ситуаций считаются до игры в большую матрицу, и во время игры остаётся только обращаться к ней, выбирая нужные значения.
Читать полностью »
ExcelArt – изометрия «на халяву». Рисуем псевдообъемный телефон без 3D и Фотошопа
2016-09-08 в 13:24, admin, рубрики: 3d, Excel, Блог компании Mail.Ru Group, графика, графический дизайн, изометрия, иллюстрация, Работа с 3D-графикой, рисование
Возможно ли получить псевдообъемное изображение без 3D-программ? «Конечно, — скажете вы, — берешь, напрягаешься и рисуешь с нуля». А если без «берешь, напрягаешься и рисуешь»? А если вообще без каких-то специальных знаний? Можно ли получить изометрические объекты, не тратя время на рендер? Существует ли вообще цифровая иллюстрация вне привычных графических программ? На эти и другие вопросы я дам ответ в своей статье, посвященной новому методу создания цифровых иллюстраций — ExcelArt.
Читать полностью »
Как делать простые анимации строительства в стратегических играх
2015-01-23 в 18:08, admin, рубрики: game development, анимация строительства, изометрия, никто не читает теги, Работа с анимацией и 3D-графикой, стратегические игрыВо многих типах игр, не только стратегических, у вас есть участок земли, и на нём нужно что-то строить. Знакомая схема, не правда ли?
Как только вы перетаскиваете постройку из «магазина» на участок, она некоторое время строится. Обычно в это время там видна одна картинка, похожая на стройплощадку. Чтобы сэкономить память и бюджет, во многих играх нарисовано три таких «стройплощадки», под разные здания: маленькая, средняя и большая. Как только строительство закончено, стройплощадка превращается в готовое здание.
Но что, если вы хотите более тонкие анимации, чтобы было видно, как здание постепенно растёт к небу?
Читать полностью »