Всем привет! Недавно возникла практическая необходимость использовать интерполяцию для замкнутых кривых. Проект разрабатывался под .Net на C#, а готовых реализаций алгоритма я не обнаружил, впрочем, как и для других языков и технологий. В результате пришлось самому изучить мат.часть существующих методов и написать свою библиотеку. Наработками и готовым решением готов поделиться с вами.
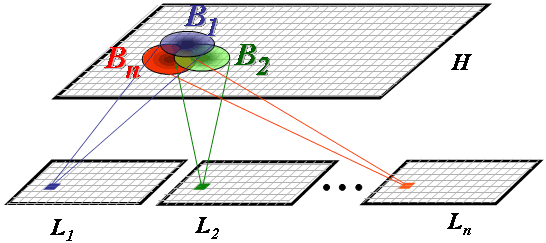
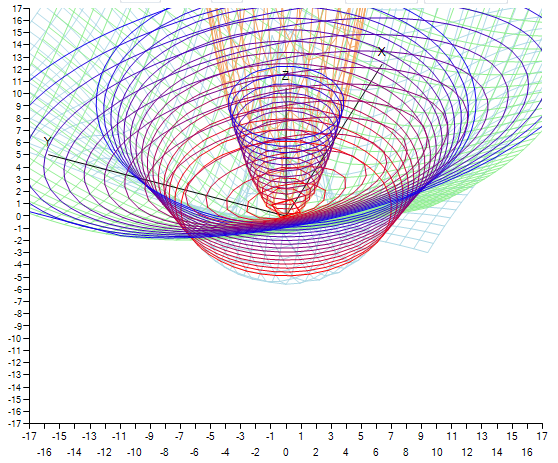
В этой статье мне бы хотелось рассказать об одном интересном математическом приеме, который будучи весьма интересным и полезным мало известен широкому кругу людей, занимающихся компьютерной графикой.
Сколько существует разных способов представить обыкновенный поворот в трехмерном пространстве? Большинство людей, когда-либо занимавшихся 3D-графикой или 3D-моделированием, сходу назовут три основных широко распространенных варианта:
Люди с богатым опытом добавят сюда почему-то не пользующийся популярностью четвертый пункт:
Мне бы хотелось рассказать о пятом способе представления вращений, который симпатичен тем, что удобен для параметризации, позволяет эффективно строить полиномиальные аппроксимации этих параметризаций, проводить сферическую интерполяцию, и главное, универсален — с минимальными изменениями он работает для любых видов движений. Если вам когда-либо был нужен метод, который позволял бы легко сделать «аналог slerp, но не для чистых вращений, а для произвольных движений, да еще и с масштабированием», то читайте эту статью. Читать полностью »
Доброго времени суток, харбачитатель.
В этой статье мне хотелось бы рассказать об одном придуманном когда-то алгоритме (или скорее всего — переизобретённом велосипеде) построенного плавного графика по заданным точкам, используя кривые Безье. Статья была написана под влиянием вот этой статьи и очень полезного комментария товарища lany, за что им отдельное спасибо.
Постановка задачи
Есть массив Y-ков точек, расположенных равномерно по оси X. Нужно получить плавный график, который проходит через все заданные точки. Пример на рисунке ниже:
Всех, кому интересно, прошу под кат.
Читать полностью »
Добрый день, всем!
За последние годы работы в среде LabVIEW приходилось иметь дело с разными задачами, решение которых вытекало в создание простых и не очень простых виртуальных приборов(ВП). Специализация моей работы – это проектирование различных алгоритмов для анализа биомедицинских сигналов. И как у любого разработчика за несколько лет у меня накопилось большое количество кода разной сложности. Для всех виртуальных приборов, которые по той или иной причине мне жалко было удалять, я создал папку, куда и сохранял все. В данной статье мне хотелось бы привести некоторую выборки из моего LabVIEW-портфолио.
Выборка имеет достаточно эклектичный характер, и многие приборы опытные разработчики могут воспроизвести сами за несколько минут. Поэтому, полагаю данная статья может пригодится в основном для начинающих LabVIEW-разработчиков. Большинство представленного кода можно так или иначе найти на LabVIEW – форумах или в экземплах среды. Исходники прилагаю в конце статьи (версия 9.0).
В начале хотелось бы привести пару ВП, которые относятся к разряду очень простых, но возможно кому-то необходимых.
Читать полностью »
Совершенно случайно я превратился из питониста в JS-разработчика, и на мою хрупкую детскую психику обрушился непосильный груз вещей, которых в JS нет. Например, нет удобного форматирования строк. На питоне можно написать:
'hello, %(thing)s' % {'thing': 'world'}
Или вот так:
'hello, {thing}'.format(**{'thing': 'world'})
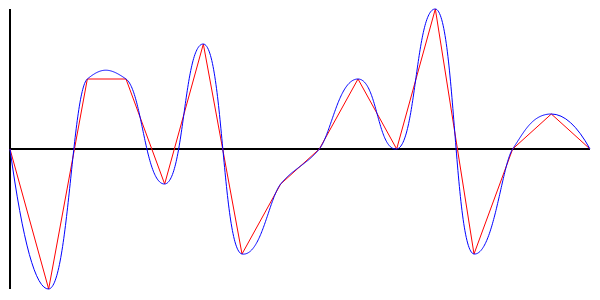
-shkala--s-.png "Интерполяция + (линейная | логарифмическая) шкала + С++")
Понадобилось мне как-то сделать интерфейс для загрузки в микроконтроллер график функции «сопротивление -> температура» (график решили задавать по нескольким точкам, а потом их интерполировать). По ходу дела выяснилось, что график будет оч-чень нелинейным (180 Ом -> 100o, 6 000 Ом -> 0o, 30 000 Ом -> -30o). Поэтому пришлось мне погрузиться в тему логарифмических шкал… и сразу вынырнуть, так как я не нашел того, что мне нужно. А нужно-то мне было всего лишь понять математику (и реализацию на С++) таких дел. ЧуднО — вроде такая нужная тема, а не расписано! Ну да ладно — мозги заскрипели и вспомнили высшую математику из университета, и программа была написана. Решил описать я свои мытарства тут — может, кому пригодится.
В этой статье я распишу теорию (а также базовые виртуальные классы), в следующей возьмусь за конкретные реализации средствами Qt.
Осторожно: в тексте много графики!
Читать полностью »
В обработке изображений существует класс методов Super-resolution (SR), которые позволяют качественно увеличить разрешение исходного изображения, при этом происходит преодоление оптического предела объектива и/или физического разрешения цифрового сенсора, который записал изображение.
Алгоритмы SR используют два подхода для вычисления результирующего изображения: 1) на базе множества кадров одного объекта; 2) самообучающаяся система с базой образцов.
Статья представляет собой нечто вроде “практического руководства” для построения весьма интересных трехмерных графиков функций вида z=f(x,y), с примером реализации на C#.
Читать полностью »
