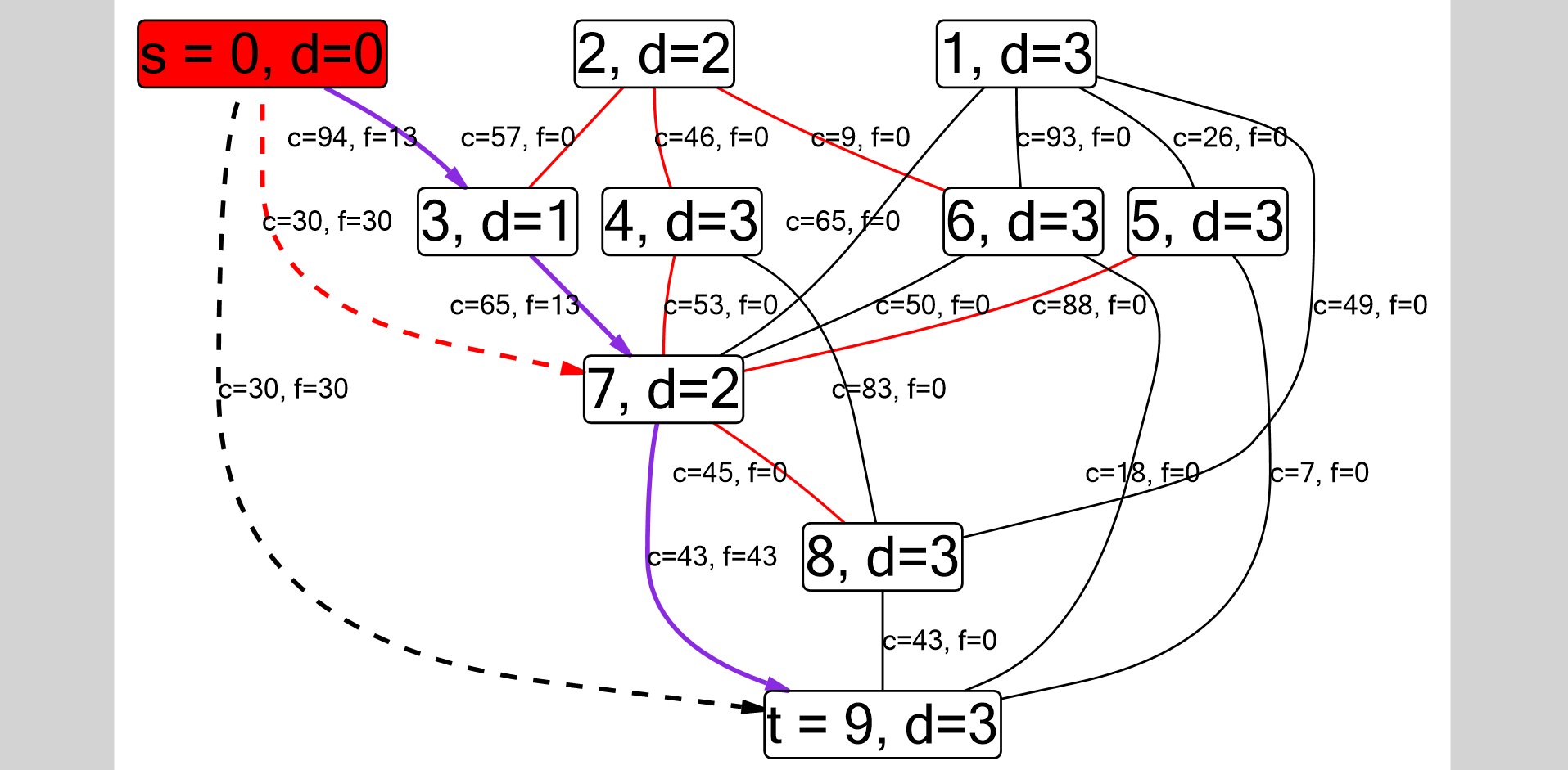
Представим типичную ситуацию на первом курсе: вы прочитали про алгоритм Диница, реализовали, а он не заработал, и вы не знаете, почему. Стандартное решение — это начать отлаживать по шагам, каждый раз рисуя текущее состояние графа на листочке, но это жутко неудобно. Я попробовала исправить положение в рамках семестрового проекта по Software Engineering, а в посте расскажу, как у меня в итоге получился плагин для Visual Studio. Скачать можно тут, исходный код и документацию можно посмотреть тут. Вот скриншот графа, который получился для алгоритма Диница.
Рубрика «графы» - 4
Отладка алгоритмов на графах — теперь с картинками
2019-07-26 в 14:49, admin, рубрики: hse, Visual Studio, Visual Studio extension, vs, алгоритмы на графах, Блог компании Питерская Вышка, визуализация, визуализация данных, вшэ, графы, отладка, питерская вышка, плагин, ПрограммированиеСпециалисты по информатике расширяют рубежи проверяемого знания
2019-07-18 в 7:00, admin, рубрики: IP, mip, neexp, np, графы, квантовая физика, квантовые компьютеры, квантовые технологии, математикаВселенная задач, проверяемых компьютером, выросла. Благодаря какому секретному ингредиенту это произошло? Из-за квантовой запутанности.

Представьте, что некто пришёл к вам и заявил, что у него есть оракул, способный раскрыть сокровенные тайны вселенной. Вы могли бы заинтересоваться этим, но вам тяжело было бы в это поверить. Вы бы хотели придумать способ подтвердить, что оракул говорит правду.
Такова основная проблема информатики. Некоторые задачи слишком сложно решить за разумное время. Но их решения просто проверить. Учитывая это, специалистам по информатике хочется знать: насколько сложной может быть задача, решение которой всё ещё можно проверить?
Оказывается, что ответ на этот вопрос: практически невообразимо сложной.
Читать полностью »
Элемент нулевого размера
2019-06-16 в 9:18, admin, рубрики: Анализ и проектирование систем, графы, изобретение, инженерные системы, комбинаторика, Научно-популярное, проектирование, ТРИЗ, функция
Графы — схематическое обозначение во многих сферах.
Модель реальных объектов.
Круги — вершины, линии — дуги графа (соединения).
Если рядом с дугой цифра — это расстояние между точками на карте или стоимость на диаграмме Ганта.
В электрике и электронике вершины — это детали и модули, линии — проводники.
В гидравлике котлы, бойлеры, арматура, радиаторы и трубы.
На карте — города и дороги.
Из школьной задачи по математике:
Из пункта А в пункт Б выехал автобус. Расстояние между пунктами 30 км.
А что если расстояние 0?
Читать полностью »
Оптимизация поиска в ширину: как обработать граф с 10 миллиардами состояний
2019-06-11 в 6:27, admin, рубрики: breadth-first search, Алгоритмы, алгоритмы поиска, головоломки, графы, Игры и игровые приставки, оптимизация кода, поиск в ширину, поисковые технологии, Программирование
Пару месяцев назад мне наконец пришлось признать, что я недостаточно умён, чтобы пройти некоторые уровни головоломки Snakebird. Единственным способом вернуть себе часть самоуважения было написание солвера. Так я мог бы притвориться, что создать программу для решения головоломки — это почти то же самое, что и решить её самому. Код получившейся программы на C++ выложен на Github. Основная часть рассматриваемого в статье кода реализована в search.h и compress.h. В этом посте я в основном буду рассказывать об оптимизации поиска в ширину, который бы потребовал 50-100 ГБ памяти, чтобы он уместился в 4 ГБ.
Позже я напишу ещё один пост, в котором будет описана специфика игры. В этом посте вам нужно знать, что мне не удалось найти никаких хороших альтернатив грубому перебору (brute force), потому что ни один из привычных трюков не сработал. В игре множество состояний, потому что есть куча подвижных или толкаемых объектов, при этом важна форма некоторых из них, которая может меняться со временем. Не было никакой пригодной консервативной эвристики для алгоритмов наподобие A*, позволяющих сузить пространство поиска. Граф поиска был ориентированным и заданным неявно, поэтому одновременный поиск в прямом и обратном направлении оказался невозможным. Единственный ход мог изменить состояние множеством несвязанных друг с другом способов, поэтому не могло пригодиться ничего наподобие хеширования Зобриста.
Приблизительные подсчёты показали, что в самой большой головоломке после устранения всех симметричных положений будет порядка 10 миллиардов состояний. Даже после упаковки описания состояний с максимальной плотностью размер состояния составлял 8-10 байт. При 100 ГБ памяти задача оказалась бы тривиальной, но не для моей домашней машины с 16 ГБ памяти. А поскольку Chrome нужно из них 12 ГБ, мой настоящий запас памяти ближе к 4 ГБ. Всё, что будет превышать этот объём, придётся сохранять на диск (старый и ржавый винчестер).
Читать полностью »
Жизнь до рантайма. Доклад Яндекса
2019-06-02 в 10:06, admin, рубрики: AST, dependency injection, javascript, runtime, webpack, Блог компании Яндекс, графы, интерфейсы, Промышленное программирование, системы сборки, технический долгВ большом проекте может возникнуть задача идентификации изменений для конечного пользователя по отличиям в коде фронтенда приложения. Разработчик из Яндекс.Маркета Никита Сидоров рассказал, как мы решали эту проблему при помощи библиотеки Diffector, о построении и анализе графа модулей в Node.js-приложениях и о поиске дефектов в коде до его запуска.
— Сегодня я постараюсь быть с вами максимально откровенным. Читать полностью »
«Игра престолов»: строим инфографику об убийствах, сексе, путешествиях по Вестеросу и многое другое
2019-05-13 в 17:09, admin, рубрики: game of thrones, wolfram language, wolfram mathematica, Блог компании Wolfram Research, визуализация данных, гистограмма, графы, диаграмма, Занимательные задачки, игра престолов, Инфографика, Программирование
Оригинал поста + Вспомогательные функции и исходные данные
Оглавление
Взаимоотношения персонажей
— Кто кого родил
— Кто кому брат или сестра
— Кто кого убил
— Кто кому служит
— Кто с кем женат или помолвлен
— У кого с кем был секс
— Все отношения на одном графе
Связь персонажей по сценам
Кто самый «популярный» персонаж Игры престолов?
— Количество экранного времени у персонажей
— Сколько персонажей было в сериях?
— Кто из персонажей был самом большом количестве серий «Игры престолов»?
Самые популярные локации «Игры престолов»
— Карта локаций «Игры престолов»
— Перемещения персонажей «Игры престолов» от серии к серии
— Кто больше всего «путешествовал» из персонажей «Игры престолов»?
— Самые популярные локации «Игры престолов» (по экранному времени)
В каких фильмах ещё играли актёры Игры престолов и насколько они знакомы?
— Фильмы, в которых играли самые «востребованные» актёры «Игры престолов»:
— Актёры «Игры престолов» в «Гарри Поттере»
— Актёры «Игры престолов» в «Звёздных войнах»
— Актёры «Игры престолов» в «Пиратах карибского моря»
— В каких фильмах/сериалах много актёров «Игры престолов»
— Как тесно связаны между собой актёры «Игры престолов»
Разговоры в «Игре престолов»
Пол персонажей «Игры престолов»: кого больше, мужчин или женщин?
В этом посте я расскажу о том, как применять язык Wolfram Languge в анализе и визуализации данных на примере базы данных по «Игре престолов». В этой статье не уделяется особого внимания парсингу данных, об этом я расскажу отдельно. Вместо этого пост целиком посвящен интересной инфографике и её созданию.
Надеюсь, что построенные визуализации заинтересуют тех, кому нравится этот замечательный сериал).
Читать полностью »
«Топологическая» сортировка графа с циклами
2019-05-10 в 16:25, admin, рубрики: linux, Алгоритмы, графы, дискретная математика, математика, оптимизация программПолное название статьи должно было звучать как «Устойчивая „топологическая“ сортировка графа с циклами за O(|V| + |e| log |e|) по времени и O(|V|) по памяти без рекурсии», но мне сказали что это перебор.
Читать полностью »
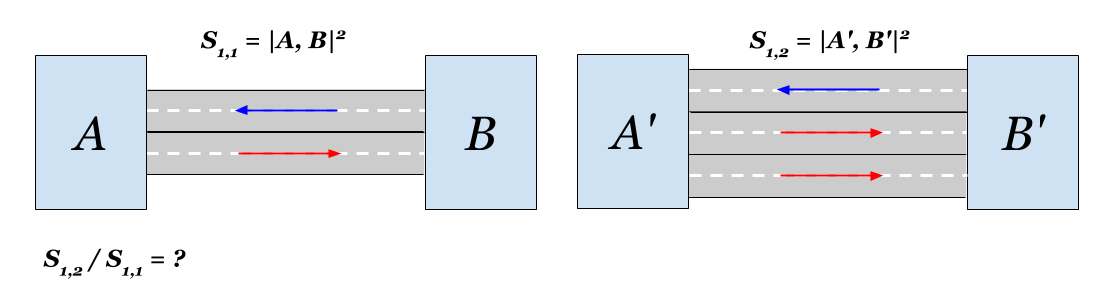
О близости вершин
2019-04-16 в 9:21, admin, рубрики: близость, графы, математика, метрика, расстояние«До того, как вы постигнете это, оно кажется чудом. Но после в нем нет ничего особенного.»
Не, не про горы, — про графы. В математике есть вопросы, формулировка которых доступна каждому, а вот решение нетривиально и без специальной подготовки трудно объяснимо. Одну из подобного рода проблем кратко можно выразить так — как правильно считать расстояния в направленных графах? Данную несколько абстрактную проблему можно свести к вполне конкретной мотивирующей задаче. Она умещается на одном рисунке:
Использование графов для решения разреженных систем линейных уравнений
2019-02-04 в 2:32, admin, рубрики: Алгоритмы, графы, математика, прямые решатели, разреженные матрицы, численные методыПрелюдия
Численное решение линейных систем уравнений является незаменимым шагом во многих сферах прикладной математики, инженерии и IT-индустрии, будь то работа с графикой, расчёт аэродинамики какого-нибудь самолёта или оптимизация логистики. Модная нынче «машинка» без этого тоже не особо бы продвинулась. Причём решение линейных систем, как правило, сжирает наибольший процент из всех вычислительных затрат. Понятно, что эта критическая составляющая требует максимальной оптимизации по скорости.
Часто работают с т.н. разреженными матрицами — теми, у которых нулей на порядки больше остальных значений. Такое, например, неизбежно, если имеешь дело с уравнениями в частных производных или с какими-нибудь другими процессами, в которых возникающие элементы в определяющих линейных соотношениях связаны лишь с «соседями». Вот возможный пример разреженной матрицы для известного в классической физике одномерного уравнения Пуассона 
Противоположные им матрицы — те, в которых на количество нулей не обращают внимания и учитывают все компоненты без исключения, — называют плотными.
Читать полностью »
SciPy, алгоритмы на графах
2019-02-01 в 11:45, admin, рубрики: Dijkstra's algorithm, python, scipy, sparse matrix, text, word ladder, графы, математика
SciPy (произносится как сай пай) — это пакет прикладных математических процедур, основанный на расширении Numpy Python. Он значительно расширяет возможности Python, предоставляя в распоряжение пользователя команды и классы высокого уровня для управления данными и их визуализацией. С SciPy интерактивный сеанс Python превращается в такую же полноценную среду обработки данных и прототипирования сложных систем, как MATLAB, IDL, Octave, R-Lab и SciLab.