
Шипастики повсюду
Мы зовём его «Шипастиком» [Spikey], и в своей сегодняшней жизни я встречаюсь с ним постоянно:

Он происходит от трёхмерного объекта, многогранника под названием «ромбический шестидесятигранник».
Читать полностью »

Мы зовём его «Шипастиком» [Spikey], и в своей сегодняшней жизни я встречаюсь с ним постоянно:

Он происходит от трёхмерного объекта, многогранника под названием «ромбический шестидесятигранник».
Читать полностью »
Кто не любил в детстве собирать конструкторы? Я до сих пор помню эту красную коробочку с кучей металлических деталей, инструментов и морем возможных результатов лишь бы была фантазия, время и желание. LEGO тоже не стоит забывать, хоть тут все было чуть проще и гораздо красочнее. Но вот что сложнее и того и другого так это конструкторы наноструктур на базе ДНК-оригами. До сих пор все «детальки» подобных конструкций моделировались вручную, что занимало уйму времени и сил. Представьте, что все детали LEGO вам нужно создавать самому, прежде чем собрать их в гигантского робота с лазерами, реактивными двигателями и пулеметом на плече. Но что-то детские воспоминания увели нас не в ту степь.
Шутки в сторону. Сегодня мы с вами познакомимся с алгоритмом, позволяющим автоматически создавать ДНК-оригами достаточно разнообразной формы. Ранее изменение формы нитей ДНК до необходимой выполнялось вручную, что сильно ограничивало возможности подобной процедуры. Данный же алгоритм позволяет создавать детали ДНК конструктора автоматически, что позволяет в дальнейшем использовать их для формирования двумерных и трехмерных наноструктур. Плюс этот алгоритм доступен всем желающим. Доклад исследовательской группы поможет нам разобраться что и как работает. Поехали.Читать полностью »
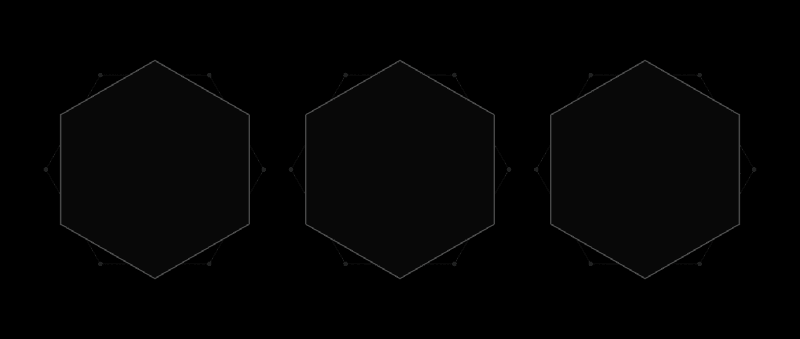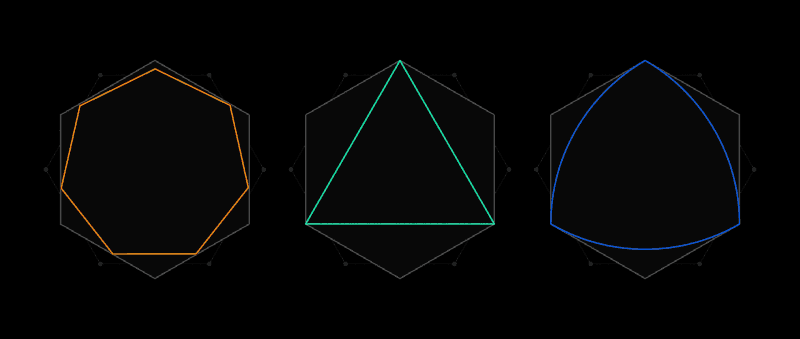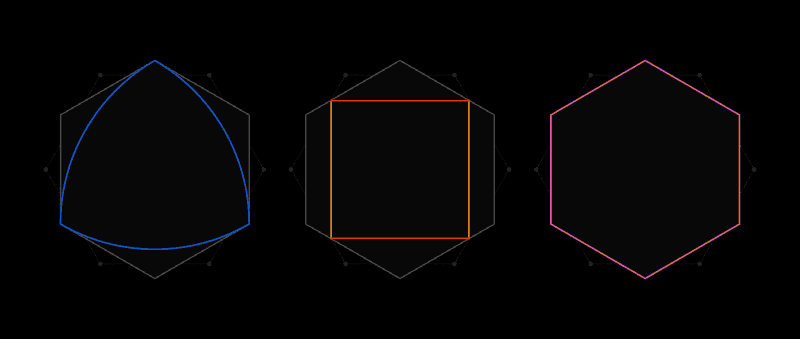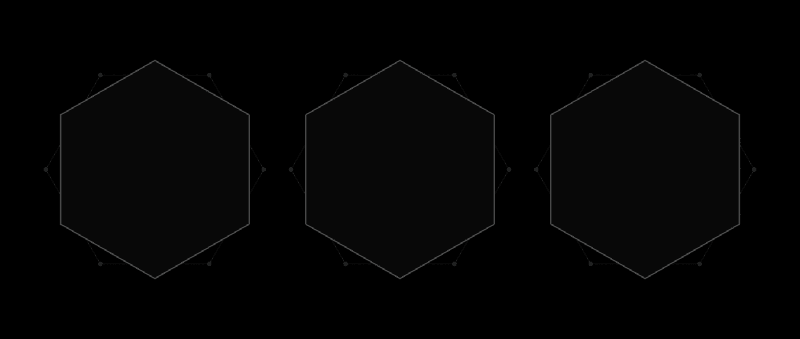
Такое универсальное покрытие, как шестиугольник, можно описать вокруг любой формы
Филип Гиббс – не профессиональный математик. Поэтому когда ему хотелось поразмышлять над какой-либо задачей, он искал такую, с которой может справиться и любитель. Он обнаружил трудную задачу, которая может свести с ума даже лучшие умы. И в работе, опубликованной в этом году, Гиббс значительно продвинулся в решении вопроса столетней давности, зависящего от способности точно измерять площадь вплоть до атомных масштабов.
Первым эту задачу предложил французский математик Анри Леон Лебег, в письме к своему другу Юлиусу Палу, написанному в 1914 году. Лебег спросил: какова форма наименьшей возможной площади, способной полностью покрыть большое количество других форм (имеющих одно общее свойство, о котором ниже)?
Читать полностью »
Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.
Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.
Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).
Наслаждайтесь. И не говорите, что врач не предупреждал.
Читать полностью »

Не только Стоунхендж, но и другие мегалитические сооружения создавались древними обитателями Британских островов с пониманием основ геометрии
Теорему, о которой идет речь в заголовке, в школе учили все. Даже самые нерадивые ученики слышали имя Пифагора и понимают суть теоремы. Утверждение, что в прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы действительно не слишком сложное для понимания. Считается, что впервые теорему сформулировал древнегреческий философ и математик, который жил на острове Самос в VI-V веках до нашей эры.
Но вполне может быть, что эту же теорему использовали жители Британских островов задолго до Пифагора. Они жили за 2000 лет до рождения философа и математика, так что рассказать им о геометрии было некому — все вычисления проводились собственными силами. Скорее всего, знания того времени формировались эмпирическим путем. Об этом говорится в книге «Megalith: Studies in Stone».
Читать полностью »

Подобно своему создателю Карлу Вейерштрассу, это чудовище возникло из ниоткуда. Потратив четыре года учёбы в университете на кутежи и фехтование, Вейерштрасс выпустился из него с пустыми руками. В конце концов он взялся за преподавание и бо́льшую часть 1850-х был школьным учителем в Браунсберге. Ему была отвратительна жизнь в маленьком прусском городишке, он находил своё существование там одиноким. Единственной отдушиной для него стали математические задачи, над которыми он работал между уроками. Но ему не кем было поговорить о математике, и у него не было технической библиотеки для обучения. Даже результатам его работ не удавалось покинуть пределов Браунберга. Вместо публикации в академических журналах, как это сделал бы университетский исследователь, Вейерштрасс добавлял их к школьным проспектам, пугая потенциальных учеников заумными уравнениями.
В конце концов Вейерштрасс отправил одну из своих статей в уважаемый «Журнал Крелле». Несмотря на то, что предыдущие статьи остались едва замеченными, эта вызвала огромный всплеск интереса. Вейерштрасс обнаружил способ работы с ужасным классом уравнений, известным как «абелевы функции». В статье было приведено краткое изложение его методов, но этого было достаточно, чтобы убедить математиков в наличии у автора уникального таланта. Не прошло и года, как Кёнигсбергский университет дал Вейерштрассу почётную докторскую степень, а вскоре после этого Берлинский университет предложил ему должность профессора. Несмотря на то, что Вейерштрасс проделал интеллектуальный аналог пути «из грязи в князи», многие из его старых привычек сохранились. Он редко публиковал статьи, предпочитая делиться своими работами со студентами. Но он был малопочтителен не только к процессу публикации: не пугали его и «священные коровы» математики.
Читать полностью »

Ребёнком, попадая на побережье штата Орегон, я часто думал: «Насколько широк океан и что там, за горизонтом?» Взрослея, я обратил свой взор к ночному небу, и думал о чём-то похожем: «Как далеко находятся звёзды, и есть ли у них другие планеты?» И хотя мало кто из нас совершал кругосветные путешествия, и ни один человек ещё не отправлялся в космос дальше Луны, мы знаем ответы на некоторые из этих вопросов. Необъятность можно измерить. И хотя эти огромные числа в повседневной жизни имеют мало смысла, мы хотя бы знаем, что они нам известны.
Представьте, каково было бы жить в мире, в котором это не так: где ощущение необъятности, уверенность в наличии необъяснимого, было бы общепринятым, а мысль о познаваемости мира была бы в новинку. Философ Анаксагор родился примерно за 500 лет до н.э. в восточном Средиземноморье, там, где теперь находится турецкое побережье. К тому времени философия совсем недавно обратилась к изучению природного мира. Менее, чем за сто лет до этого, Фалес Милетский якобы предсказал солнечное затмение, что закончило войну, и доказал, что наш мир был предсказуемым, а все события не являются простой прихотью богов.
Читать полностью »
Всем привет! Когда-то давным-давно я делал простенькие игрушки на Flash. Например: игрушка — провести курсор мышки через лабиринт, не касаясь стен и уворачиваясь от всяких движущихся объектов. Некоторые из этих объектов двигаются по заданной траектории, некоторые гонятся за курсором, а некоторые стреляют в курсор другими движущимися объектами.
Сейчас я увлёкся программированием под андроид и сделал примерно такую же игрушку. И столкнулся с теми же геометрическими задачками с которыми встречался тогда.
Вот что строил испанский архитектор Антонио Гауди:

Его здания описывают как «бионические дома», некоторые говорят о «летящей пластичной материи». За морем восторгов художников и дизайнеров, как мне показалось, упущена некоторая невероятная рационализация и прагматичность. Гауди был в первую очередь отличным разработчиком, математиком и геометром. Но чтобы объяснить это, сначала я покажу другую картинку:

Это два крепления. Первое производится серийно — оно просто в проектировании, просто в изготовлении, дёшево и невероятно уродливо. Второе красивое, и требует на 25% меньше материала для того, чтобы выдержать тот же вес (то есть — куда прочнее). Только его трудно рассчитать, оно будет дороже в серии — и придётся подумать.
Примерно то же самое делал Гауди. Ему пришлось обойтись без математического аппарата и современных материалов. И ещё действовать в рамках строго ограниченного бюджета. Он, фактически, заложил новые принципы всего от фасада до последней дверной ручки, создал шедевры оптимизации — в общем смёл все стереотипы как сухие листья, создал с нуля теорию и воплотил её. В девятнадцатом веке всё то, что он делал, было просто диким. Некоторые даже считали его сумасшедшим. Читать полностью »
Наткнулась на эту задачу совершенно случайно. У меня знакомая через год после окончания магистратуры снова решила учиться и начала готовиться к поступлению. А значит что-то нужно просто повторить и вспомнить, ну и разобраться с чем-то новым. Вот сидела она над какой-то задачей, я проходила мимо. Задача показалась весьма простой (школьного уровня), но надо немного подумать.
Итак, рассматриваемая здесь задача звучит так: даны угол и точка внутри него. Через эту точку провести отрезки, имеющие концы на сторонах угла, так, чтобы полученный треугольник имел наименьший периметр.
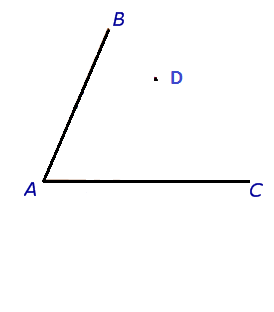
Читать полностью »