Приветствую Вас, уважаемые Читатели! Сегодня хочу поговорить об открытом недавно удивительном доказательстве теоремы Пифагора. Да-да, Вы не ослышались!
Рубрика «геометрия» - 2
Это невозможное доказательство теоремы Пифагора нашли в 2023 году
2023-04-22 в 16:32, admin, рубрики: геометрия, доказательство, математика, пифагорКак мы написали курс планиметрии
2023-04-16 в 12:23, admin, рубрики: геометрия, геометрия на плоскости, математика, Профессиональная литератураШкольная мечта
Удивительные кубы Хинтона, которые позволяют каждому увидеть четырехмерный мир
2023-04-09 в 1:35, admin, рубрики: Биографии гиков, геометрия, измерения, математика, наука, фантастикаПриветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать Вам о замечательном популяризаторе математики Чарльзе Говарде Хинтоне - человеке, внесшем просто огромный вклад в дело изучения объектов четырехмерного мира.
Зачем, спрашивается, их изучать? Я, для начала, ограничусь цитатой его тезки Говарда Лавкрафта, произведения которого я не так давно очень полюбил:
Левон Сергеевич Атанасян — автор главного учебника по геометрии для школьников
2022-01-07 в 16:34, admin, рубрики: Биографии гиков, биография, геометрия, математика, Научно-популярное, преподавание в университете, преподаватель, учебник, ученые, учёный, Читальный залПролог
Паутина для чайников: алгоритм строительства паучьих сетей
2021-11-05 в 12:00, admin, рубрики: Алгоритмы, биология, Блог компании ua-hosting.company, геометрия, математика, машинное обучение, Научно-популярное, нити, пауки, паутина, сети, строительство, хищники, членистоногие, шёлк, эволюция
К паукам можно относиться как угодно: их можно бояться, недолюбливать или держать в качестве питомцев. Но любой, от арахнофоба до арахнолога, согласится с тем, что они мастера по строительству своих сетей. Научное сообщество уже очень давно и с большим интересом наблюдает за членистоногими прядильщиками, но полностью раскрыть все их секреты пока еще не удалось. И вот ученые из университета Джонса Хопкинса (США) решили детально рассмотреть и описать процесс строительства паутины, используя при этом искусственный интеллект и приборы ночного видения. Выяснилось, что разные виды пауков подчиняются общим правилам в ходе создания своих сетей. Следовательно, наблюдение за движениями лапок может предсказать, что именно будет строить паук. На какие стадии можно разделить строительство паутины, как пауки ведут себя во время каждой из них, и как эти данные могут помочь в понимании нас самих? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.Читать полностью »
Учёные раскрыли универсальную геометрию геологии, и оказалось, что мир состоит из кубов
2020-12-18 в 10:35, admin, рубрики: гёмбёц, геология, геометрия, Диаграммы Вороного, математика, Научно-популярное, физикаУпражнения в чистой математике привели к созданию масштабной теории об устройстве мира
Где-то в середине лета 2016 года венгерский математик Габор Домокош взошёл на крыльцо дома Дугласа Джерольмака, геофизика из Филадельфии. С собой у Домокоша были дорожные чемоданы, сильная простуда и жгучая тайна.
Чуть позже двое мужчин гуляли по гравийной дорожке на площадке за домом, где жена Джерольмака держала тележку для продажи тако. Под их ногами хрустел измельчённый известняк. Домокош указал под ноги.
«Сколько граней у каждого из этих камушков?» – спросил он. Затем он ухмыльнулся. «Что, если я скажу вам, что их количество обычно равно шести?» А затем он задал ещё более общий вопрос, который, как он надеялся, надолго поселится в мозге его коллеги. Что, если мир состоит из кубов?
Читать полностью »
Некоторые математические задачи нерешаемы, и это не так уж плохо
2020-12-03 в 7:00, admin, рубрики: Алгоритмы, геометрия, математика, Научно-популярное
Постройте выпуклый восьмиугольник с четырьмя прямыми углами.
Вероятно, то, что я даю такие задания, многое говорит обо мне, как об учителе. Я наблюдаю за тем, как студенты пытаются выстроить прямые углы последовательно. Когда у них это не получается, они пытаются перемежать прямые углы. Снова потерпев неудачу, они вставляют их в многоугольник случайным образом. Скрежет, издаваемый их мозгами во время мыслительных усилий — музыка для ушей учителя.
Потом у них возникают подозрения и они начинают задавать вопросы. «Вы сказали о прямых углах. Может, на самом деле вы имели в виду три угла?», «Вы точно имели в виду выпуклый многоугольник?», «Четыре прямых угла, по сути, образуют прямоугольник. Как мы можем получить ещё четыре стороны в восьмиугольнике?» Я внимательно слушаю, киваю, подтверждая их догадки.
Читать полностью »
Быстрый поиск касательных и пересечений у выпуклых многоугольников
2020-11-15 в 14:39, admin, рубрики: Алгоритмы, выпуклые полигоны, геймдев, геометрия, касательные, математика, поиск пути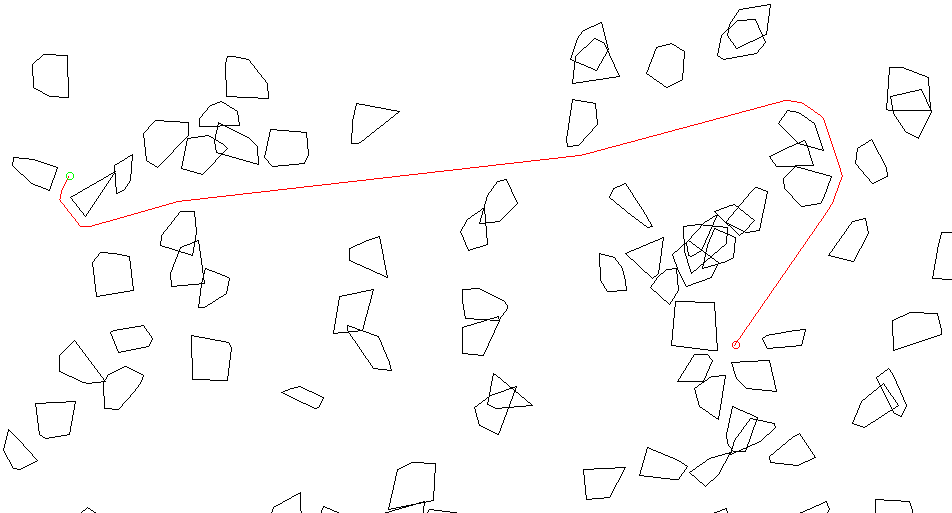
Я недавно сделал маленькую библиотеку для решения задачи поиска кратчайшего пути на 2D карте с выпуклыми препятствиями. В процессе реализации я придумал пару алгоритмов и трюков, описания которых я нигде не встречал. Поэтому делюсь этими "изобретениями" с общественностью.
Горжусь тем, что мое решение работает очень быстро. Для внушительного количества полигонов все операции можно выполнять каждый кадр. Т.е. не надо ничего запекать и вся геометрия карты может меняться в каждом кадре.
OpenCASCADE и Невидимое солнце Дао
2020-09-09 в 14:36, admin, рубрики: cad, CAD/CAM, OpenCascade, python, WebGL, геометрия, Инь, Работа с 3D-графикой, стереометрия, Янь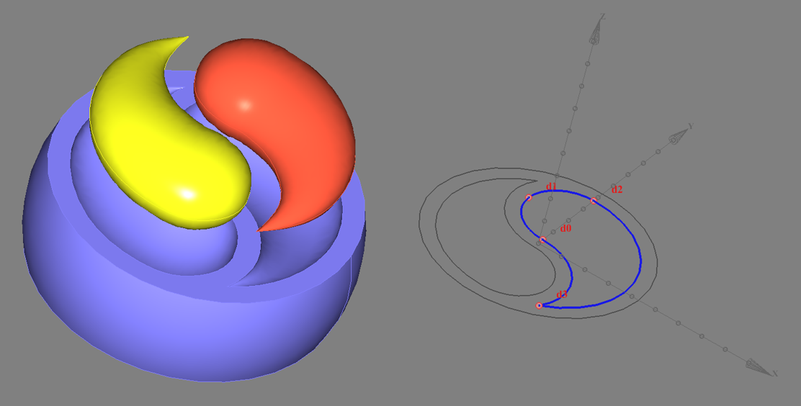
Тот лучший путник, что следов не оставляет
Тот лучший лидер, что без речи вдохновляет
План совершенен, если плана вовсе нет
И если мудрый двери закрывает,
Вам никогда не разгадать секрет.
Великая книга Дао - Стих 27 ( Перевод Ю. Полежаевой)
Бумажный бит: создание механической памяти из оригами
2020-08-28 в 6:50, admin, рубрики: 0 и 1, биты, Блог компании ua-hosting.company, бумага, геометрия, двоичная система счисления, математика, механика, Научно-популярное, оригами, память, переключатели, физика, хранение данных, Читальный зал
«Бегущий по лезвию», «Воздушная тюрьма», «Heavy Rain» — что общего между этими представителями массовой культуры? Во всех в той или иной степени присутствует древнее японское искусство по складыванию бумаги — оригами. В кино, играх и в реальной жизни оригами частенько используется в качестве символа определенных чувств, каких-то воспоминаний или своеобразного послания. Это скорее эмоциональная составляющая оригами, но с точки зрения науки в бумажных фигурках сокрыто множество интересных аспектов из самых разных направлений: геометрия, математика и даже механика. Сегодня мы с вами познакомимся с исследованием, в котором ученые из Американского института физики создали устройство хранения данных за счет складывания/раскладывания фигурок оригами. Как именно работает бумажная карта памяти, какие принципы в ней реализованы и сколько данных может хранить такое устройство? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.Читать полностью »