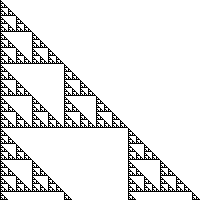На хабре уже много-много-много раз писали про игру «Жизнь». Совсем недавно была удивительная статья Жизнь на плоскости Лобачевского. Но игра «Жизнь» является частным случаем т. н. клеточных автоматов. Существует много других клеточных автоматов совсем не похожих на игру «Жизнь», но тем не менее очень интересных. Про некоторые из них и хочется рассказать здесь.
Начнём с того, что рассмотрим ряд клеток, в которых, кроме одной, находятся нули:
... 0 1 0 0 0 0 0 0 ...
Рассмотри следующее правило, заменяем число в клетке на сумму этого числа и соседа слева. Получим следующую серию состояний:
... 0 1 0 0 0 0 0 0 ...
... 0 1 1 0 0 0 0 0 ...
... 0 1 2 1 0 0 0 0 ...
... 0 1 3 3 1 0 0 0 ...
... 0 1 4 6 4 1 0 0 ...
... 0 1 5 10 10 5 1 0 ...
... 0 1 6 15 20 15 6 1 ...
Не сложно увидеть, что это — треугольник Паскаля. А теперь вместо обычного сложения будем использовать сложение по модулю два. Известно (и даже недавно рассказывалось в хабрастатье Треугольник Серпинского и треугольник Паскаля), что получится дискретный аналог треугольника Серпинского:
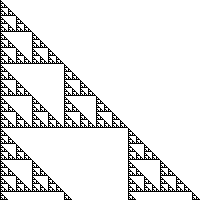
... 0 1 0 0 0 0 0 0 ...
... 0 1 1 0 0 0 0 0 ...
... 0 1 0 1 0 0 0 0 ...
... 0 1 1 1 1 0 0 0 ...
... 0 1 0 0 0 1 0 0 ...
... 0 1 1 0 0 1 1 0 ...
... 0 1 0 1 0 1 0 1 ...
Интересно? Читаем дальше!
Читать полностью »