Стандартная гауссова статистика работает на основе следующих предположений. Центральная предельная теорема утверждает, что при увеличении числа испытаний, предельное распределение случайной системы будет нормальным распределением. События должны быть независимыми и идентично распределены (т.е. не должны влиять друг на друга и должны иметь одинаковую вероятность наступления). При исследовании крупных комплексных систем обычно предполагают гипотезу о нормальности системы, чтобы далее мог быть применен стандартный статистический анализ.
Рубрика «фрактал» - 2
RS-анализ (анализ фрактальной структуры временных рядов)
2015-04-22 в 13:04, admin, рубрики: Алгоритмы, временной ряд, математика, размерность, фрактал, ХерстВерблюды, бабочки и фрактальный хаос теоретической экологии
2014-12-05 в 21:49, admin, рубрики: Биотехнологии, детерминированный хаос, измерения, научная фантастика, Научно-популярное, физика, фрактал, Читальный зал, экологияПриветствую почтенных Гиков! Счастье, как известно, это «когда тебя понимают». А с этим часто бывают проблемы. Особенно, если ты работаешь в лаборатории над темой «методы анализа состояний детерминированного хаоса в динамике растительного покрова», а тебя просят в двух словах рассказать чем ты занимаешься на работе. Под катом, моя попытка изложить в простом и понятном виде один из самых интересных аспектов теоретической экологии.
Проектирование СШП шестиугольной фрактальной микрополосковой НЕантенны, или будь бдителен
2014-10-10 в 12:14, admin, рубрики: антенна, Беспроводные технологии, моделирование, радиосвязь, фрактал 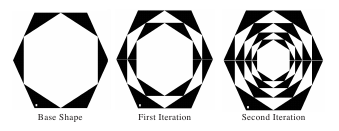
В последние несколько лет я регулярно сталкиваюсь с задачами по разработке СШП (сверхширокополосных) СВЧ-модулей и функциональных узлов. И как ни грустно мне об этом говорить, но почти всю информацию по теме я черпаю из зарубежных источников. Однако некоторое время назад, в поисках нужной мне информации, я наткнулся на очень интересную статью, сулившую решение всех моих проблем. О том, как решения проблем не получилось, я и хочу рассказать.
Читать полностью »
Приключения в математическом лесу фрактальных деревьев
2014-09-30 в 10:32, admin, рубрики: wolfram language, wolfram mathematica, математика, Программирование, тернарные деревья, фрактал, фрактальные деревья 
Перевод поста Bernat Espigulé Pons, «Adventures into the Mathematical Forest of Fractal Trees».
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.
Без сомнения, золотое сечение и в наше время представляется одним из самых таинственных, волшебных и поразительных чисел, которые известны людям: 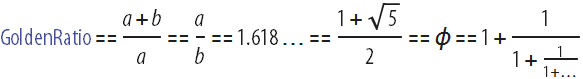 . (в языке Wolfram Language и системе Mathematica ему соответствует символ GoldenRatio). Как вы увидите из этого поста, это число действительно имеет множество интересных свойств, которые можно исследовать, причём некоторые из них рассматривались ещё в работах учёных Древней Греции, таких как Пифагор и Евклид, другие в работах итальянского математика Леонардо Пизанского, более известного под прозвищем Фибоначчи, или Иоганном Кеплером — астрономом эпохи Возрождения. Хотя это может прозвучать странно, в этом посте я расскажу вам о новых геометрических объектах, связанных с золотым сечением, которые осветили мне путь, когда я пытался отобразить неизвестную ранее область Математического Леса.
. (в языке Wolfram Language и системе Mathematica ему соответствует символ GoldenRatio). Как вы увидите из этого поста, это число действительно имеет множество интересных свойств, которые можно исследовать, причём некоторые из них рассматривались ещё в работах учёных Древней Греции, таких как Пифагор и Евклид, другие в работах итальянского математика Леонардо Пизанского, более известного под прозвищем Фибоначчи, или Иоганном Кеплером — астрономом эпохи Возрождения. Хотя это может прозвучать странно, в этом посте я расскажу вам о новых геометрических объектах, связанных с золотым сечением, которые осветили мне путь, когда я пытался отобразить неизвестную ранее область Математического Леса.
Читать полностью »
Вычисление фрактальной размерности Минковского для плоского изображения
2014-01-08 в 15:23, admin, рубрики: Алгоритмы, Компьютерное зрение, математика, машинное обучение, фрактал, метки: Компьютерное зрение, машинное обучение, фрактал  Доброго времени суток читатель. Сегодняшний пост будет посвящен вычислению приближенного значения фрактальной размерности плоского изображения, которая тесно связано с размерности Минковского. Это интересно как минимум по двум причинам. Во-первых оказывается, что размерность ограниченного множества в метрическом пространстве может быть не только целым числом, но и любым не отрицательным. Во-вторых значение размерности контура изображения (а это ограниченное множество в метрическом пространстве) является хорошим признаком. В рамках сегодняшнего поста не предусмотрено исследование робастности этого признака, но давайте рассмотрим показательный пример. Множество различных характеристик клеток опухолей молочной железы, полученное в результате анализа снимков тонкоигольной пункционной биопсии. Множество данных состоит из 30 признаков (поля таблицы) с пометкой злокачественная или доброкачественная опухоль, и одним из признаков является как раз фрактальная размерность ядер клеток опухоли. Под катом вас ждет объяснение смысла фрактальной размерности множества, по возможности доступным языком, алгоритм вычисления приближенного значения этой размерности, его реализация на c# и ряд примеров с картинками. Возможно вы открыли этот пост только из-за картинки справа, это изображение я позаимствовал из инстаграмма Jennifer Selter, и в конце мы вычислим фрактальную размерность, так сказать филейной части Дженифер. Хочется кстати вас попросить ответить на пару вопросов в конце поста.
Доброго времени суток читатель. Сегодняшний пост будет посвящен вычислению приближенного значения фрактальной размерности плоского изображения, которая тесно связано с размерности Минковского. Это интересно как минимум по двум причинам. Во-первых оказывается, что размерность ограниченного множества в метрическом пространстве может быть не только целым числом, но и любым не отрицательным. Во-вторых значение размерности контура изображения (а это ограниченное множество в метрическом пространстве) является хорошим признаком. В рамках сегодняшнего поста не предусмотрено исследование робастности этого признака, но давайте рассмотрим показательный пример. Множество различных характеристик клеток опухолей молочной железы, полученное в результате анализа снимков тонкоигольной пункционной биопсии. Множество данных состоит из 30 признаков (поля таблицы) с пометкой злокачественная или доброкачественная опухоль, и одним из признаков является как раз фрактальная размерность ядер клеток опухоли. Под катом вас ждет объяснение смысла фрактальной размерности множества, по возможности доступным языком, алгоритм вычисления приближенного значения этой размерности, его реализация на c# и ряд примеров с картинками. Возможно вы открыли этот пост только из-за картинки справа, это изображение я позаимствовал из инстаграмма Jennifer Selter, и в конце мы вычислим фрактальную размерность, так сказать филейной части Дженифер. Хочется кстати вас попросить ответить на пару вопросов в конце поста.
Быстрый взлом RSA
2013-12-21 в 13:05, admin, рубрики: Исследования и прогнозы в IT, криптография, математика, фрактал, метки: фракталRSA — криптографический алгоритм основанный на вычислительной сложности разложения числа на простые множители (факторизация). Решая задачу факторизации за полиномиальное время мы, собственно, сможем взламывать RSA. Пока такую задачу, теоретически, можно решить на основе кубитов. А что если мы фундаментально неправильно подходим к самой сути математики?

Треугольник Серпинского и треугольник Паскаля
2013-01-31 в 14:44, admin, рубрики: математика, Паскаль, треугольник, фрактал, метки: Паскаль, треугольник, фракталЧто это?
Треугольник Серпинского
Треугольник Серпинского — один из известнейших фракталов, его построение — одна из первых лабораторных работ на рекурсию по соответствующим дисциплинам во многих ВУЗах. Выглядит фрактал следующим образом:

Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси.
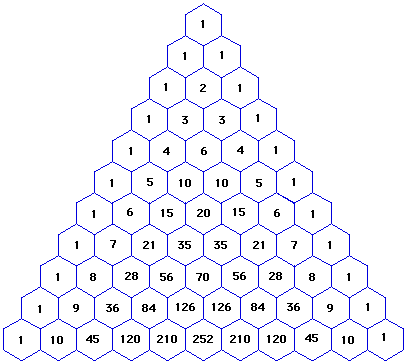
И что с того?
Есть в треугольнике Паскаля интересная особенность. Читать полностью »
Построение фрактальных фигур в Matlab
2012-12-16 в 16:49, admin, рубрики: Matlab, математика, фрактал, хаос, метки: Matlab, фрактал, хаос«Итерация от человека. Рекурсия — от Бога.» Л. Питер Дойч
Введение
Многие из нас слышали про фракталы, я думаю, что многие даже имеют довольно четкое представление об этих удивительных математических объектах и их тесной взаимосвязи с физическими природными структурами. Тем не менее, в этой статье я хотел бы затронуть исследовательский и философский аспекты данного вопроса. Сама по себе возможность генерировать сложнейшие узоры на комплексной плоскости с помощью простых математических выражений весьма заманчива, собственно это и натолкнуло на написание статьи. Написав пару строчек кода мы сможем упасть на самое дно разрядной сетки нашего ПК, изучая масштабируемые фрактальные узоры.
Читать полностью »

