Серия «Белый шум рисует черный квадрат»
История цикла этих публикаций начинается с того, что в книге Г.Секей «Парадоксы в теории вероятностей и математической статистике» (стр.43), было обнаружено следующее утверждение:

Рис. 1.
По анализу комментарий к первым публикациям (часть 1, часть 2) и последующими рассуждениями созрела идея представить эту теорему в более наглядном виде.
Большинству из участников сообщества знаком треугольник Паскаля, как следствие биноминального распределения вероятностей и многие сопутствующие законы. Для понимания механизма образования треугольника Паскаля развернем его детальнее, с развертыванием потоков его образования. В треугольнике Паскаля узлы формируются по соотношению 0 и 1, рисунок ниже.
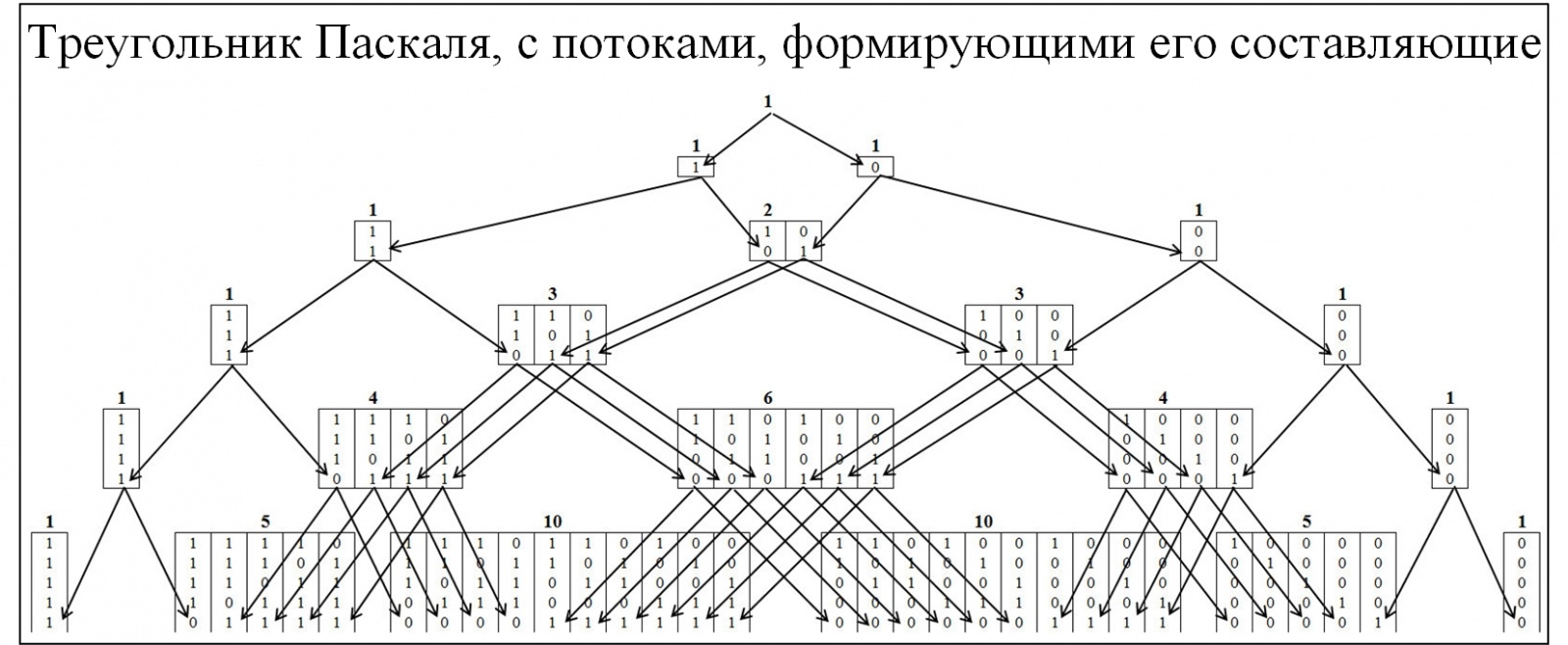
Рис. 2.
Для понимания теоремы Эрдёша-Реньи составим аналогичную модель, но узлы будут формироваться из значений, в которых присутствуют наибольшие цепочки, состоящие последовательно из одинаковых значений. Кластеризации будет проводиться по следующему правилу: цепочки 01/10, к кластеру «1»; цепочки 00/11, к кластеру «2»; цепочки 000/111, к кластеру «3» и т.д. При этом разобьём пирамиду на две симметричные составляющие рисунок 3.

Рис. 3.
Первое что бросается в глаза это то, что все перемещения происходят из более низкого кластера в более высокий и наоборот быть не может. Это естественно, так как если цепочка размера j сложилась, то она уже не может исчезнуть.
Читать полностью »



