Это вторая часть серии статей, посвящённой построению числовых систем, основанных на упорядоченных парах (целые, рациональные, гауссовы, двойные, дуальные...). В предыдущей статье мы рассмотрели как строится кольцо целых чисел из пары натуральных, освоившись с понятиями классов эквивалентности и факторизацией. В этой построим ещё одну знакомую числовую систему: поле рациональных чисел.
Рубрика «факторизация»
Математическая продлёнка. Изобретаем дроби
2024-11-27 в 13:32, admin, рубрики: рациональные дроби, теория чисел, факторизация, эквивалентные классыМатематическая продлёнка. Изобретаем целые числа
2024-11-26 в 19:23, admin, рубрики: теория представлений, теория чисел, факторизация, целые числа, эквивалентные классыВ этой мини-серии статей я хочу объединить свои заметки для математического кружка о различных необычных, но полезных числовых системах, основанных на парах чисел. План знакомства с числовыми системами будет такой:
-
В этой статье мы (признаюсь, достаточно занудно) построим из натуральных чисел целые, при этом познакомимся с важнейшими инструментами математики: упорядоченной парой, эквивалентностью и факторизацией.
-
Во второй части от целых мы перейдём к рациональным числам, которые тоже можно представить в виде пары — Читать полностью »
Старая математика ломает постквантовые шифры
2023-01-29 в 13:30, admin, рубрики: NIST, SIKE, Блог компании GlobalSign, информационная безопасность, квантовая криптография, кривые второго порядка, криптография, математика, Научно-популярное, постквантовые шифры, теорема Кани, теорема ферма, факторизация, эллиптические кривыеСтарая математика ломает постквантовые шифры
Мир криптографии постепенно готовится к приходу квантовых вычислений, где вместо двоичной логики используются кубиты. Предполагается, что именно криптография станет одним из первых применений квантовых компьютеров.
Проблема в том, что современные алгоритмы вроде RSA и Диффи-Хеллмана (в том числе на эллиптических кривых) не способны противостоять квантовым атакам. Поэтому в июле 2022 года Национальный институт стандартов и технологий США (NIST) опубликовал набор алгоритмов шифрования, потенциально способных противостоять взлому на квантовых компьютерах — так называемые «постквантовые шифры».
Один из «постквантовых» шифров сразу взломали. Но самое интересное — метод, который применили исследователи.
Читать полностью »
Криптография после высадки инопланетян
2018-09-21 в 16:06, admin, рубрики: алгоритм Гровера, алгоритм Шора, Алгоритмы, дискретное логарифмирование, инопланетяне-математики, информационная безопасность, квантовая криптография, криптография, математика, научная фантастика, односторонние функции, факторизация, функции с потайным входомАвтор статьи: Брюс Шнайер — американский криптограф, писатель и специалист по компьютерной безопасности. Автор нескольких книг по безопасности, криптографии и ИБ. Основатель криптографической компании Counterpane Internet Security, Inc., член совета директоров Международной ассоциации криптологических исследований и член консультативного совета Информационного центра электронной приватности.
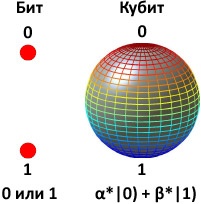Квантовые вычисления — это новый способ производить расчёты, который позволит человечеству выполнять вычисления, просто невозможные с использованием современных компьютеров. Возможность быстрого поиска сломает некоторые из современных алгоритмов шифрования. А лёгкая факторизация больших чисел сломает криптосистему RSA с любой длиной ключа.
Именно поэтому криптографы сейчас усиленно разрабатывают и анализируют «квантово-устойчивые» алгоритмы с открытым ключом. В настоящее время квантовые вычисления пока не готовы для нормальной оценки: что безопасно, а что нет. Но если предположить, что инопланетяне разработали технологию в полном объёме, то квантовые вычисления — не конец света для криптографии. Для симметричной криптографии квантово-устойчивость обеспечить элементарно, а сейчас мы ищем квантово-стойкие алгоритмы шифрования с открытым ключом. Если криптография с открытым ключом окажется временной аномалией, которая существует благодаря пробелам в наших математических знаниях и вычислительных способностях, мы всё равно выживем. И если какая-то немыслимая инопланетная технология сломает всю криптографию, у нас останется секретность, основанная на теории информации, пусть и со значительными потерями возможностей.
Читать полностью »
Серьезная уязвимость в популярной библиотеке шифрования подрывает безопасность миллионов крипто-ключей
2017-10-16 в 16:07, admin, рубрики: безопасность, Блог компании Positive Technologies, информационная безопасность, криптография, уязвимости, факторизация
Изображение: crocs.fi.muni.cz
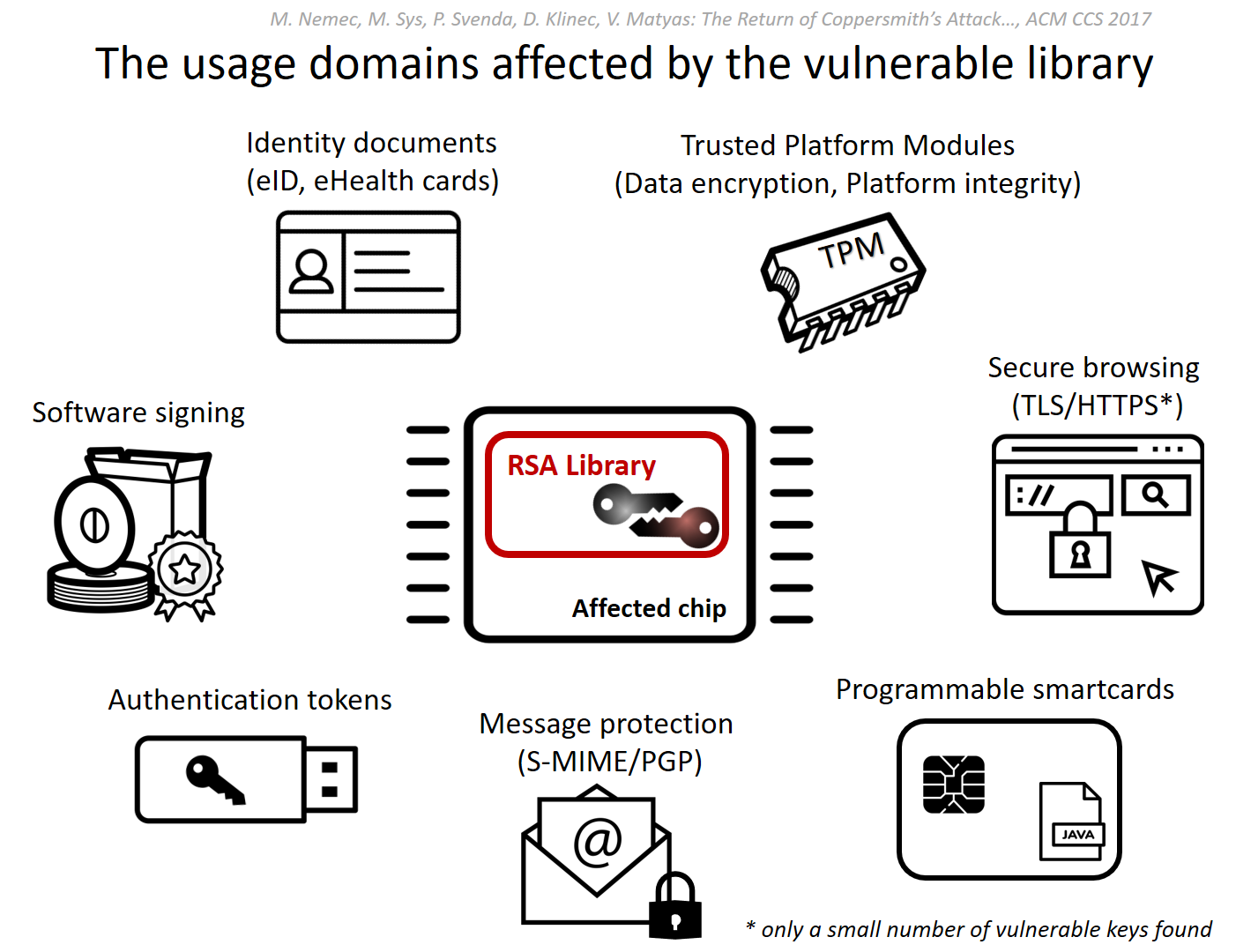
Международная группа исследователей информационной безопасности из Великобритании, Словакии, Чехии и Италии обнаружила критическую уязвимость в популярной библиотеке шифрования RSA Library v1.02.013 от Infineon. Ошибка в алгоритме для генерации простых чисел RSA, делает сгенерированные с помощью библиотеки Infineon ключи шифрования подверженными факторизации — это позволяет злоумышленникам раскрывать секретную часть ключа.
Уязвимая библиотека применяется для обеспечения безопасности национальных ID-карт в нескольких странах, а также во многих популярных программных продуктах, используемых как государственными органами, так и бизнесом.Читать полностью »
Быстрое вычисление факториала — PrimeSwing
2017-04-28 в 21:03, admin, рубрики: primeswing, Алгоритмы, математика, простые числа, факториал, факторизация, метки: primeswing, факториалНаткнувшись недавно на эту статью, я понял, что редко упоминаются способы вычисления факториала, отличные от банального перемножения последовательных чисел. Нужно эту ситуацию исправить.
Предлагаю рассмотреть «асимптотически наиболее быстрый» алгоритм вычисления факториала!Читать полностью »
Анализ эффективности метода факторизации на эллиптических кривых. Практика
2017-02-09 в 12:03, admin, рубрики: Алгоритм Ленстры, Алгоритмы, математика, факторизация, эллиптические кривые, метки: факторизацияПроблема факторизации напрямую связана с определением криптостойкости RSA, которое базируется на предположении, что не существует быстрых алгоритмов факторизации, которые за короткое время позволили бы взломать код, а если через некоторое время и получится это сделать, то данные потеряют свою актуальность. В этой статье мы протестируем и сделаем выводы по одному из способов факторизации.
Читать полностью »
Непростые простые числа: секреты тайного общества ткачей
2015-04-11 в 14:16, admin, рубрики: Алгоритмы, криптография, математика, многомерные матрицы, особое мнение, простые числа, факторизацияНепростые простые числа
Автор статьи предлагает заглянуть в то, что представляют собой множества простых чисел, если взглянуть на них геометрическим образом. Это не профессиональная работа, а простое, любительское исследование некоторых любопытных закономерностей. Поэтому, в статье не будет сложной математики, и мы не будем забираться глубоко в ее дебри.
Вероятно, читателю известны многие проблемы, связанные с простыми числами. Их расположение в множестве натуральных чисел неочевидно. Большие простые числа трудно находить, нужно много усилий, чтобы проверить большое число на простоту. На этой трудности основаны многие современные методы криптографии. Мы можем легко перемножить да многозначных простых числа, но зная результат найти исходные множители – очень сложная задача.
Есть множество способов оптимизации, которые намного быстрее простого перебора, однако даже если оптимизация ускорит поиск в 10 раз, достаточно увеличить число на 2-3 десятичных знака (например, в 100 раз), чтобы замедлить поиск в 10^100 раз.
Это и значит, что сложность алгоритма является экспоненциальной, и поэтому какой бы быстрый ни был суперкомпьютер, мы можем подобрать длину числа еще больше, чтобы таких суперкомпьютеров потребовалось миллиард. Правда, стоит уточнить еще раз: находить простые числа для перемножения при этом становится так же все труднее и труднее.
К слову, математики не нашли ни доказательства, ни опровержения того, что нельзя найти алгоритм факторизации, сложность которого не была бы экспоненциально зависящей от длины числа. А доказав или опровергнув это, можно, заодно, решить математическую проблему, известную как гипотеза Римана. За ее доказательство математический институт Клея обещает миллион долларов.