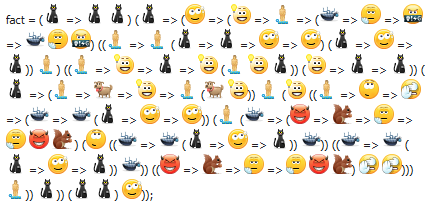Рубрика «факториал»

в 8:01, , рубрики: pic, timeweb_статьи, датчик холла, домофон, катушка, ключи, компаратор, магнит, мультиплексор, сейф-сервис, тапки, факториал, феррит
Приветствую всех!

Думаю, многим из нас хорошо известно, что в ныне применяемых домофонных ключах, хоть их иногда называют магнитными, никаких магнитов на деле нет.

Но так было далеко не всегда. В девяностые, когда электронные замки стали постепенно распространяться, существовало огромное количество совершенно экзотических типов ключей. И вот ко мне в руки попал очередной крайне интересный экземпляр, устройством которого стоит поделиться.

image

Итак, в сегодняшней статье поговорим о ферритовых домофонных ключах. Узнаем, как же они считываются, как устроена панель. Традиционно будет много интересного.Читать полностью »

в 11:22, , рубрики: haskell, Scheme, ненормальное программирование, Программирование, факториал, функциональное программирование

Злые языки утверждают, что функциональные языки программирования — «языки для написания факториалов». Чаще всего так определяют язык Haskell, мы же начнем с того функционального языка, который сильно повлиял и на Haskell, и на подмножество средств для функционального программирования многих других языков — язык Scheme. По-крайней мере, map и for-each, filter и reduce, а так же apply и eval пришли в наши любимые языки программирования если не именно из Scheme, то в том числе и оттуда.

Рассмотрим некоторые возможные способы записи вычисления факториала. Заодно получится своеобразная ода языку программирования Scheme. Думаю, этот замечательный язык того вполне заслуживает.

У меня получилось 10 вариантов записи определений функций, которые можно свести к 3 основным способам вычисления: традиционному линейно-рекурсивному вычислительному процессу, итерации, генерации последовательности чисел с последующей сверткой умножением. Предлагаю рассмотреть эти варианты подробнее. Попутно мы рассмотрим: оптимизацию хвостовой рекурсии, функции высших порядков и метапрограммирование, отложенные вычисления, бесконечные списки, мемоизацию, способ создать статическую переменную в Scheme и гигиенические макросы.

Читать полностью »

в 7:01, , рубрики: математика, математические загадки, теория вероятностей, треугольные числа, факториал, числа каталана, числа фибоначчи

Джеймс Тэнтон разбрасывается задачками по теории чисел с той же щедростью, с которой Джон Д. Рокфеллер раздавал десятицентовики. Я уже писал об одной из задач Тэнтона. Спустя несколько недель моё внимание привлёк этот твит о факториалах и квадратах и уже не давал мне покоя:

Tweet reads: 4!+1=25, a square number. 5!+1=121, a square number. Another example? Two more examples?

«4!+1 = 25, квадрат числа. 5!+1 = 121, тоже квадрат числа. Можете привести ещё один пример? Ещё два примера?»

С помощью ручки и бумаги легко показать, что $6!$ не подходит. Факториал $6!$ — это $1 times 2 times 3 times 4 times 5 times 6=720$; прибавив $1$, получим число $721$, которое не является квадратом. (Оно раскладывается на множители как $7 times 103$.) С другой стороны, $7!$ равно $5040$, а прибавив $1$, мы получим $5041$, что равно $71^2$. Это даёт нам очень милое уравнение:
Читать полностью »

в 21:03, , рубрики: primeswing, Алгоритмы, математика, простые числа, факториал, факторизация, метки: ,

Наткнувшись недавно на эту статью, я понял, что редко упоминаются способы вычисления факториала, отличные от банального перемножения последовательных чисел. Нужно эту ситуацию исправить.
Предлагаю рассмотреть «асимптотически наиболее быстрый» алгоритм вычисления факториала!Читать полностью »

в 22:46, , рубрики: Алгоритмы, параллельное программирование, Программирование, факториал

Задачи о переборе всех возможных перестановок заданного множества сущностей возникают в программировании достаточно часто. Как известно из комбинаторики, число возможных перестановок n предметов равно попросту факториалу числа n

n! = n * (n — 1) * (n – 2) * … * 3 * 2 * 1

Факториал – достаточно быстро растущая функция, об этом говорит ее асимптотика (формула Стирлинга), хотя достаточно посмотреть на факториалы нескольких первых членов натурального ряда:

1! 1
2! 2
3! 6
4! 24
5! 120
6! 720
7! 5 040
8! 40 320
9! 362 880
10! 3 628 800
11! 39 916 800
12! 479 001 600
13! 6 227 020 800
14! 87 178 291 200
15! 1 307 674 368 000

Как видно, факториал 13-ти уже не умещается в тип данных long.

Если задаться целью найти однозначное соответствие между номером перестановки — числом в диапазоне от 1 до n! – и ее реализацией, можно натолкнуться на один очень интересный математический факт.
Читать полностью »

в 17:03, , рубрики: Алгоритмы, длинная арифметика, математика, оптимизация, Спортивное программирование, факториал

Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.

Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.

Наивный алгоритм

Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:

static BigInteger FactNaive(int n)
{
    BigInteger r = 1;
    for (int i = 2; i <= n; ++i)
        r *= i;
    return r;            
}

На моей машине эта реализация работает примерно 1,7 секунд для N=50 000.

Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Читать полностью »

в 7:47, , рубрики: 1 апреля, arrow functions, javascript, ненормальное программирование, скайп, смайлики, факториал, функциональное программирование, числа чёрча

Всем доброго утра

Факториал на числах Чёрча — теперь и в смайликах - 1

Это полностью валидный код на JavaScript.
Читать полностью »

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js