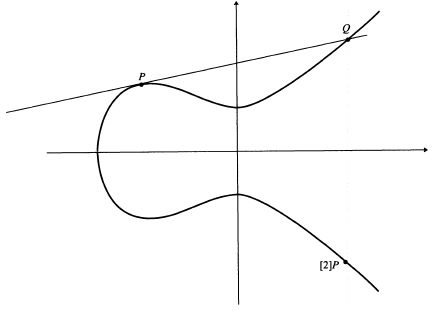
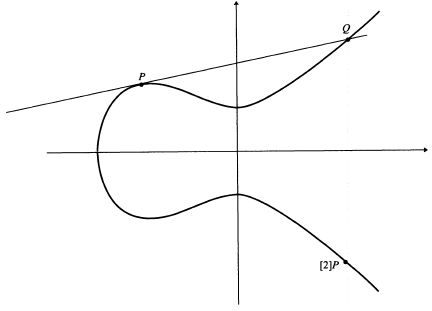
Эта примечательная гипотеза связывает поведение функции L там, где в настоящее время неизвестно, определена ли она, и порядок группы Ш, про которую неизвестно, конечна ли она!
J.T.Tate, The arithmetic of elliptic curves, Inventiones mathematicae 23 (1974)
Оригинал
This remarkable conjecture relates the behaviour of a function L at a point where it is not at present known to be defined to the order of a group Ш which is not known to be finite!
(Краткая справка насчёт актуальности цитаты 40-летней давности: после Уайлса и Ко таки стало известно, что функцию L можно определить на всей комплексной плоскости. Конечность группы Ш в общем случае остаётся неизвестной.)
Остаётся обсудить возможность ошибки. В качестве предосторожности против внутренних ошибок компьютера можно прогнать все вычисления дважды или делать проверки внутри программы. Более того, компьютеры — в отличие от людей — устроены так, что их ошибки обычно чересчур велики, чтобы их не заметить. Мы уверены, что в наших результатах нет подобных ошибок. С другой стороны, при кодировании замысловатой схемы вычислений в компьютерную программу неизбежны программистские ошибки. Большинство из них обнаруживаются ещё до основных запусков, из-за того, что программа виснет или выдаёт нелепые результаты. Но программа, которую считается работающей, всё ещё может содержать логические ошибки, проявляющиеся при редких стечениях обстоятельств: и действительно, большинство компьютеров подвержено аномалиям, из-за которых те иногда ведут себя не так, как должны по спецификациям. В сущности, наша программа для этапа (ii) оказалась неточной и пропустила очень небольшое количество эквивалентностей, которые должна была найти.
По этим причинам мы считаем, что не стоит автоматически доверять результатам, полученным на компьютере. В некоторых случаях их можно проверить за счёт свойств, которые по существу не были задействованы в вычислениях и которые вряд ли пережили бы возможную ошибку. (Например, таблицу значений гладкой функции, полученную без использования интерполяции, можно проверить вычислением разностей соседних значений.) Но если подобные проверки недоступны, не стоит полностью доверять результатам, пока они не были независимо подтверждены другим программистом на другом компьютере. Мы не думаем, что это задаёт чрезмерный стандарт во время, когда компьютеры становятся столь широко доступны; и мы уверены, что низкие стандарты уже привели к публикации и вере в неверные результаты.
B.J.Birch and H.P.F.Swinnerton-Dyer, Notes on elliptic curves. I, Journal für die reine und angewandte Mathematik 212 (1963)
Оригинал
It remains to discuss the question of error. One can take precautions against machine errors either by running all the calculations twice or by checks included in the program. Moreover, machines — unlike human beings — are so designed that the errors they make are usually too gross to be overlooked. We are satisfied that there are in our results no undetected errors of this sort. On the other hand, in translating an elaborate scheme of calculation into a machine program one is bound to make mistakes. Most of these are found before the program is used for production runs; they show up because the program grinds to a halt or produces ridiculous results. But a program which is believed to work may still contain logical errors which only have an effect in rare circumstances: and indeed most computers have anomalies which cause them occasionally not to behave in the way that their specifications suggest. In fact, our program for stage (ii) was imperfect in that a very few equivalences were missed by the machine.
For these reasons we believe that results obtained from a computer should not be automatically trusted. In some cases they can be checked because they have properties which were not essentially used in the course of the calculation and which would be unlikely to survive if an error had been made. (For example, if a table of a smooth function has been calculated without the use of interpolation, it can be checked by differencing.) But if checks of this sort are not available, results should not be fully trusted until they have been independently reproduced by a different programmer using a different machine. We do not think this sets an unreasonable standard, now that computers are becoming so widely available; and we are satisfied that lower standards have already led to a number of untrue results being published and believed.
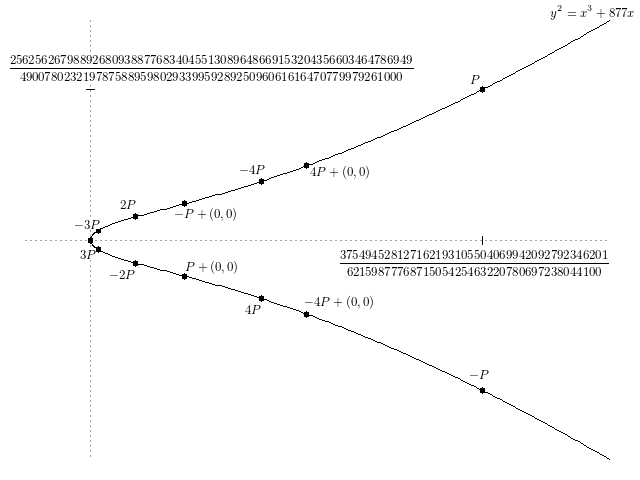
Под катом не будет формулировки гипотезы; знающие выражения вроде «Euler product» и «holomorphic continuation» (и в смысле языка, и в смысле обозначаемых понятий) могут прочитать пятистраничный pdf с сайта института Клэя. Под катом — некоторая попытка пояснить, на каком направлении развития математической мысли вообще находится гипотеза Бёрча — Свиннертон-Дайера. А также — как можно досчитать до больших чисел вроде тех, что показаны на КДПВ, менее чем за секунду.
Читать полностью »