Данная статья является продолжением предыдущей статьи о распознавании простых многоугольников по нарисованной линии. В данной части будут рассмотрены алгоритмы распознавания эллипсов и алгоритм распознавания невыпуклых многоугольников.
Рубрика «эллипс»
Распознаем фигуры по массиву точек: эллипсы и не выпуклые фигуры
2022-01-06 в 19:09, admin, рубрики: java, алгоритм, Алгоритмы, круг, массив, многоугольник, ненормальное программирование, распознавание, Точка, фигуры, эллипсПроектируем космическую ракету с нуля. Часть 5 — Первый закон Кеплера
2019-09-14 в 10:24, admin, рубрики: diy или сделай сам, задача двух тел, космонавтика, математика, Научно-популярное, первый закон кеплера, ракета, ракетостроение, физика, эллипсСодержание
Часть 1 — Задача двух тел
Часть 2 — Полу-решение задачи двух тел
Часть 3 — Ужепочти-решение задачи двух тел
Часть 4 — Второй закон Кеплера
Привет всем читателям! Сразу приступим к продолжению без лишних разглагольствований. В прошлый раз остановились на:
Это дифференциальное уравнение второго порядка, где в качестве неизвестной функции — длина радиуса вектора, зависящего от времени. Здесь 
как мы помним, может равняться нулю в случае прямолинейного движения вдоль радиус-вектора. Этот случай слишком прост, его даже рассматривать не будем, а кто хочет может приравнять в уравнении к нулю и дальше его решить.
Читать полностью »
Проектируем космическую ракету с нуля. Часть 4 — Второй закон Кеплера
2019-09-02 в 13:59, admin, рубрики: diy или сделай сам, второй закон кеплера, задача двух тел, космонавтика, математика, ракета, ракетостроение, физика, эллипсСодержание
Часть 1 — Задача двух тел
Часть 2 — Полу-решение задачи двух тел
Часть 3 — Ужепочти-решение задачи двух тел
Второй закон Кеплера
Всем привет! В прошлый раз мы остановились на вот этих уравнениях:
begin{equation*}
begin{cases}
ddot{x} = -mu dfrac{x}{(x^{2}+y^{2})^{frac{3}{2}}},
\
ddot{y} = -mu dfrac{y}{(x^{2}+y^{2})^{frac{3}{2}}}.
end{cases}
end{equation*}
Задачка теперь плоская, все будет — хорошо. Запустим численное моделирование и отрисуем несколько траекторий движения (для разных начальных условий). Не анимацию, как раньше, а чтобы видно было какие формы имеют линии:
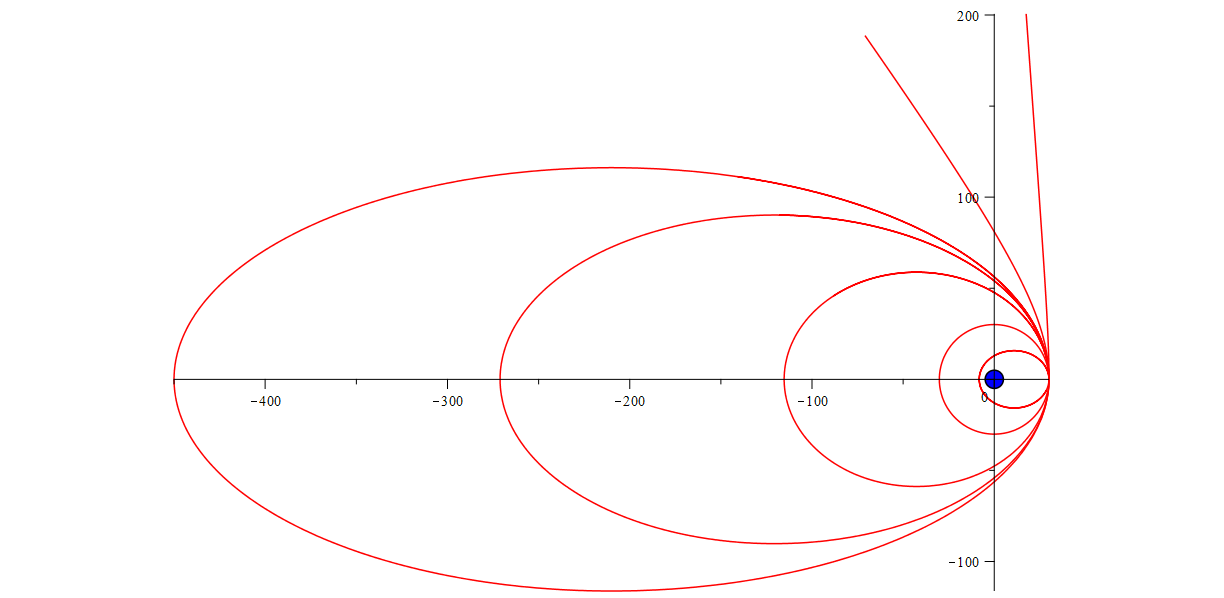
Возможные траектории движения спутника
Те кто знаком с эллипсами сразу скажут: тю, так это похоже эллипсы!
А те кто не слышал о эллипсах скажут: овал. Или сплюснутый кружок.
Читать полностью »
Астрономы нашли планету с нетипично вытянутой орбитой
2016-03-24 в 0:56, admin, рубрики: HD 20782, космонавтика, Научно-популярное, орбита, планета, эллипс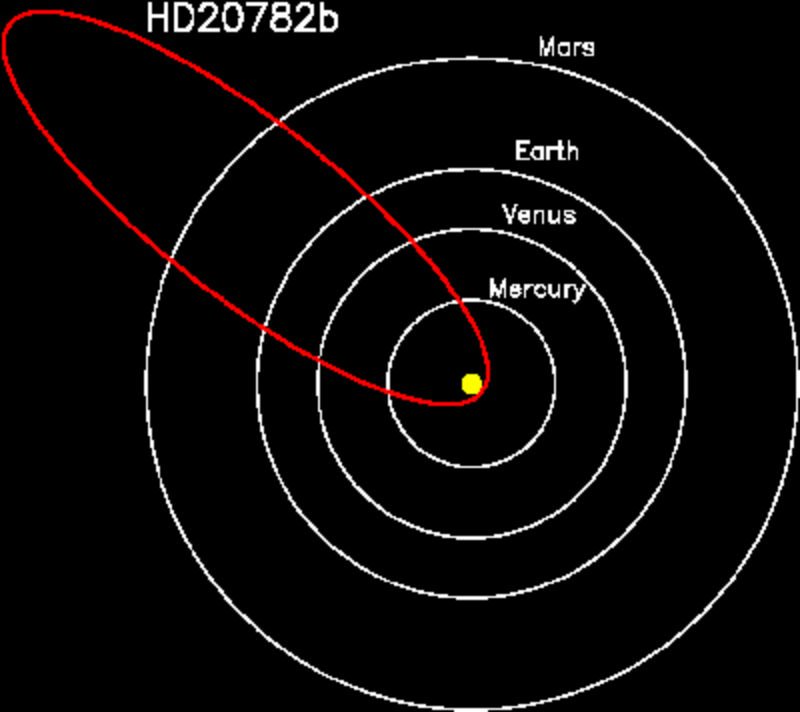 
Соотношение орбиты планеты HD 20782 с орбитами планет нашей системы
Астрономы из государственного университета Сан-Франциско обнаружили планету с крайне нетипичной орбитой. Вместо привычной орбиты, близкой к круговой, планета HD 20782 двигается по сильно вытянутому эллипсу.
Если сравнивать эту орбиту с параметрами нашей Солнечной системы, то в части её наибольшего удаления планета находится на расстоянии от своей звезды, в 2,5 раза превышающем расстояние от Земли до Солнца. Когда же планета находится ближе всего к звезде, то расстояние между ними гораздо меньше, чем расстояние от Меркурия до Солнца.
Читать полностью »
Рисование эллипса под произвольным углом в canvas на JavaScript
2015-04-10 в 14:04, admin, рубрики: canvas, javascript, векторная графика, геометрия, эллипсВ процессе разработки одного приложения столкнулся с необходимостью рисования эллипсов под произвольным углом в canvas на JavaScript. Пользоваться какими-либо фреймворками в столь простом проекте не хотелось, так что я отправился на поиски статьи-мануала на эту тему. Поиски не увенчались успехом, так что пришлось разбираться с задачей самостоятельно, и я решил поделиться с вами полученным опытом.Формализуем задачу. Нам требуется функция drawEllipse(coords, sizes, vector), где:
- coords — координаты центра эллипса — массив [x, y]
- sizes — длины большой и малой полуосей эллипса — массив [a, b]
Визуализация двумерного гауссиана на плоскости
2013-10-26 в 10:32, admin, рубрики: data mining, математика, матрица ковариации, эллипс, метки: матрица ковариации, эллипс 
Доброго времени суток. В процессе разработки одного из методов кластеризации, возникла у меня потребность визуализировать гауссиан (нарисовать эллипс по сути) на плоскости по заданной ковариационной матрице. Но я как-то сразу и не задумался, что за простой отрисовкой обычного эллипса по 4 числам скрываются какие то трудности. Оказалось, что при расчете точек эллипса используются собственные числа и собственные векторы ковариационной матрицы, расстояние Махаланобиса, а так же квантили распределение хи-квадрат, которое я, честно говоря, не использовал со времен университета ни разу.
Эллиптический спирограф
2013-06-24 в 19:36, admin, рубрики: Алгоритмы, математика, эллипс, метки: эллипсВ детстве у меня была игрушка под названием спирограф. Это такой пластмассовый лист с круглой дырой внутри, а к нему прилагались зубчатые шестеренки, тоже с дырочками, но маленькими. Ставишь ручку в дырочку, шестеренку в круг и катаешь. В результате получаются красивые кружевные узоры, которые руками ну никак не нарисуешь.
Когда я стал постарше, мне захотелось вывести такие же узоры уже на экран компьютера. Долго я думал, как это сделать, по какой формуле рисовать. А пока я думал, формулу эту вывели без меня и даже поместили ее в Википедии — рисуй не хочу. Основная идея вывода там в том, что маленький круг ездит по большому без проскальзывания, а, следовательно, расстояние, пройденное точкой с малого круга, должно равняться соответствующему расстоянию на большом круге.
Однако взятые крепости уже не манят. Естественно теперь задачу обобщить — например, сделать, чтобы маленький круг ездил внутри не окружности, а фигуры посложнее, допустим, эллипса. Читать полностью »