Рубрика «double»
Нельзя так просто взять и вычислить абсолютное значение
2021-08-16 в 5:31, admin, рубрики: double, floating point, java, абсолютное значение, математика, модуль, плавающая запятая, ПрограммированиеКажется, задача вычисления абсолютного значения (или модуля) числа совершенно тривиальна. Если число отрицательно, давайте сменим знак. Иначе оставим как есть. На Java это будет выглядеть примерно так:
public static double abs(double value) {
if (value < 0) {
return -value;
}
return value;
}Вроде бы это слишком просто даже для вопроса на собеседовании на позицию джуна. Есть ли тут подводные камни?
Алгоритм Кэхэна: как получить точную разность произведений
2019-11-14 в 7:51, admin, рубрики: double, float, fma, simd, Алгоритмы, двойная точность, математика, погрешности округления, числа с плавающей запятой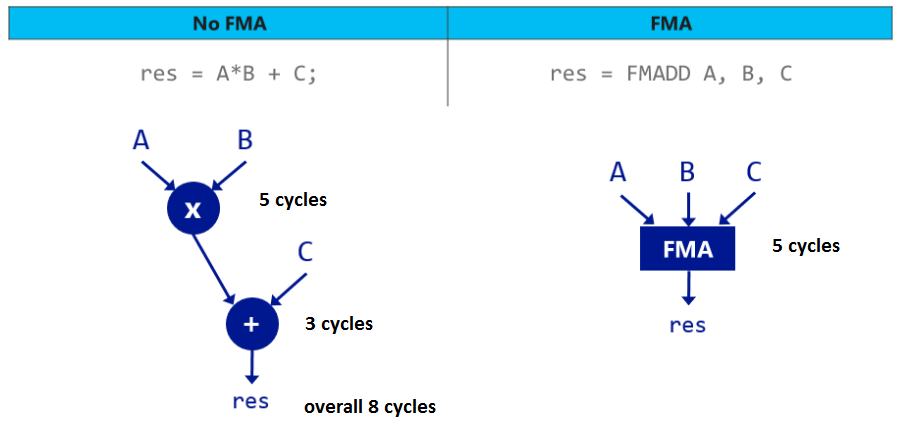
Недавно я вернулся к анализу погрешностей чисел с плавающей запятой, чтобы усовершенствовать некоторые детали в следующей редакции книги Physically Based Rendering. Числа с плавающей запятой — интересная область вычислений, полная сюрпризов (хороших и плохих), а также хитрых трюков, позволяющих избавиться от неприятных неожиданностей.
В процессе работы я наткнулся на этот пост на StackOverflow, из которого узнал об изящном алгоритме точного вычисления 
.
Но прежде чем приступать к алгоритму, нужно понять, что же такого хитрого в выражении 
? Возьмём 
, 
, 
и 
. (Это реальные значения, которые получились у меня во время запуска pbrt.) При 32-битных значениях float получаем: 
и 
. Выполняем вычитание, и получаем 
. Но если выполнить вычисления с двойной точностью, а в конце преобразовать их во float, то получится 
. Что произошло?
Проблема в том, что значение каждого произведения может сильно выйти за нижнюю границу 
, где расстояние между представимыми значениями с плавающей запятой очень велико — 64. То есть при округлении 
и 
по отдельности до ближайшего представимого float, они превращаются в числа, кратные 64. В свою очередь, их разность будет кратной 64, и не останется никакой надежды, что она станет к 
ближе, чем 
. В нашем случае результат оказался ещё дальше из-за того, как два произведения были округлены в 
. Мы напрямую столкнёмся со старым добрым катастрофическим сокращением1.
Читать полностью »
Функция Math.Sin (double) для GPU
2018-10-14 в 15:08, admin, рубрики: C#, double, gpgpu, Math.Sin, unity3d, математика, ряды ТейлораПредисловие
Мне понадобилось вычислять дугу с повышенной точностью на процессоре видеокарты в режиме реального времени.
Автор не ставил перед собой цель превзойти стандартную функцию System.Math.Sin() (C#) и ее не достиг.
Читать полностью »
Разбор перформансных задач с JBreak (часть 4)
2018-03-28 в 10:22, admin, рубрики: double, intrinsic, java, JIT-компилятор, jvm, math, Блог компании Контур, Компиляторы, оптимизация, ПрограммированиеРазбор последней четвёртой задачи:
public double octaPow(double a) {
return Math.pow(a, 8);
}
public double octaPow(double a) {
return a * a * a * a * a * a * a * a;
}
public double octaPow(double a) {
return Math.pow(Math.pow(Math.pow(a, 2), 2), 2);
}
public double octaPow(double a) {
a *= a; a *= a; return a * a;
}Условие (упрощённо):
Определить, какие методы быстрые, а какие — медленные (JRE 1.8.0_161).
Под катом бенчмарки, куски ассемблера и разбор оптимизаций со стороны JVM.
Другие публикации серии: Часть 1, Часть 2 и Часть 3.
Читать полностью »
5 правил работы с суммами
2017-09-18 в 0:30, admin, рубрики: C#, currency, decimal, double, java, платежные системы, Разработка под e-commerceВ современном программном обеспечении очень часто возникает необходимость выполнять различные операции с всевозможными суммами денег. Однако до сих пор мне нигде не попадалось документации, в которой были бы сведены воедино основные правила представления сумм и реализации финансовых вычислений. В этой статье я попробую сформулировать те правила, которые составил сам на основании личного опыта.
Одинарная или двойная точность?
2017-06-28 в 8:31, admin, рубрики: C, double, float, двойная точность, математика, одинарная точность, плавающая запятая, плавающая точка, ПрограммированиеВведение
В научных вычислениях мы часто используем числа с плавающей запятой (плавающей точкой). Эта статья представляет собой руководство по выбору правильного представления числа с плавающей запятой. В большинстве языков программирования есть два встроенных вида точности: 32-битная (одинарная точность) и 64-битная (двойная точность). В семействе языков C они известны как float и double, и здесь мы будем использовать именно такие термины. Есть и другие виды точности: half, quad и т. д. Я не буду заострять на них внимание, хотя тоже много споров возникает относительно выбора half vs float или double vs quad. Так что сразу проясним: здесь идёт речь только о 32-битных и 64-битных числах IEEE 754.
Статья также написана для тех из вас, у кого много данных. Если вам требуется несколько чисел тут или там, просто используйте double и не забивайте себе голову!
Статья разбита на две отдельные (но связанные) дискуссии: что использовать для хранения ваших данных и что использовать при вычислениях. Иногда лучше хранить данные во float, а вычисления производить в double.
Читать полностью »