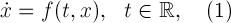Введение
Изменение курса валют на финансовом рынке влияет на цены товаров и услуг. Поэтому важно знать период времени через который цены начнут реагировать на смену курса валют.
Сложность решения указанной задачи состоит в большом количестве факторов влияющих на смену курса валют [1]. Эффективным способом отсеять ряд второстепенных факторов для определения основных тенденций рынка является применения «белого» фильтра Винера Хопфа [2,3].
Понятно, что только применение фильтра не решает всех проблем анализа влияния курса валют на финансовый рынок, однако, как один из инструментов анализа безусловно интересен. Кроме этого на примере такого фильтра можно определить коэффициенты дифференциального уравнения финансового рынка.
Постановка задачи
На основе данных о колебаниях курса валюты с использованием корреляционного анализа и системы уравнений Винера Хопфа построить динамическую модель финансового рынка при помощи которой определить временные интервалы реагирования цен на смену курса валют.
Читать полностью »