Тут на днях писали про аналитическое нахождение производных, что напомнило мне об одной моей маленькой библиотечке на C++, которая делает почти то же, но во время компиляции.
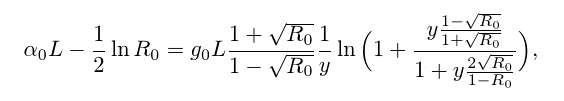
В чём профит? Ответ прост: мне нужно было запрогать нахождение минимума достаточно сложной функции, считать производные этой функции по её параметрам ручкой на бумажке было лень, проверять потом, что я не опечатался при написании кода, и поддерживать этот самый код — лень вдвойне, поэтому было решено написать штуковину, которая это сделает за меня. Ну, чтобы в коде можно было написать что-то такое:
using Formula_t = decltype (k * (_1 - r0) / (_1 + r0) * (g0 / (alpha0 - logr0 / Num<300>) - _1)); // сама формула
const auto residual = Formula_t::Eval (datapoint) - knownValue; // регрессионный остаток
// производные по параметрам:
const auto dg0 = VarDerivative_t<Formula_t, decltype (g0)>::Eval (datapoint);
const auto dalpha0 = VarDerivative_t<Formula_t, decltype (alpha0)>::Eval (datapoint);
const auto dk = VarDerivative_t<Formula_t, decltype (k)>::Eval (datapoint);
вместо крокодилов, которые получатся, если брать частные производные функции на картинке вначале (вернее, некоторого её упрощённого варианта, но он выглядит не так страшно).
Ещё неплохо быть достаточно уверенным, что компилятор это соптимизирует так, как если бы соответствующие производные и функции были написаны руками. А уверенным быть бы хотелось — находить минимум нужно было очень много раз (действительно много, где-то от сотни миллионов до миллиарда, в этом была суть некоего вычислительного эксперимента), поэтому вычисление производных было бы бутылочным горлышком, происходи оно во время выполнения через какую-нибудь рекурсию по древообразной структуре. Если же заставить компилятор вычислять производную, собственно, во время компиляции, то есть шанс, что он по получившемуся коду ещё пройдётся оптимизатором, и мы не потеряем по сравнению с ручным выписыванием всех производных. Шанс реализовался, кстати.
Под катом — небольшое описание, как оно там всё работает.
