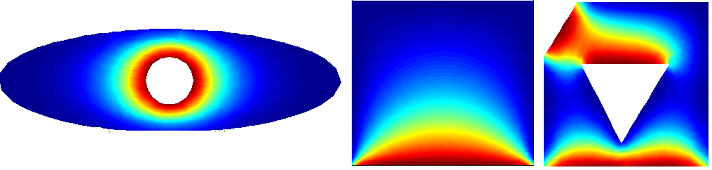
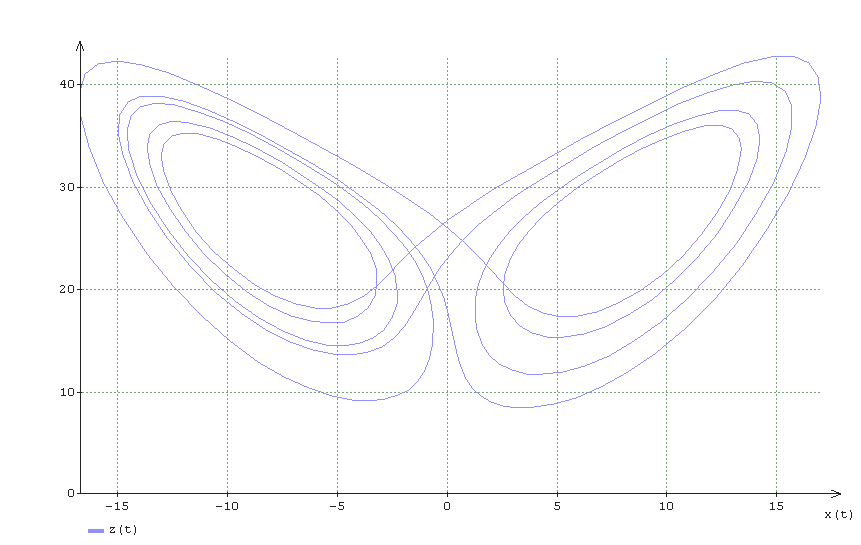
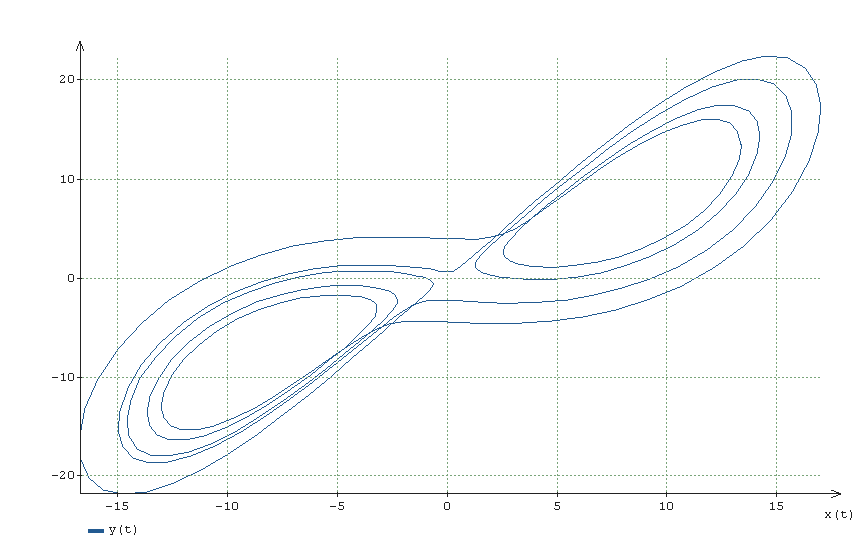
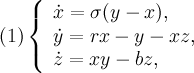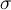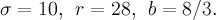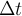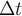Александр 4110 Шаенко (экс-инженер Даурия Аэроспейс, ныне главарь проекта краудсорсингового спутника «Маяк») и Степан Тезюничев пишут открытый софт для моделирования теплового режима спутников.
Репозиторий тут.
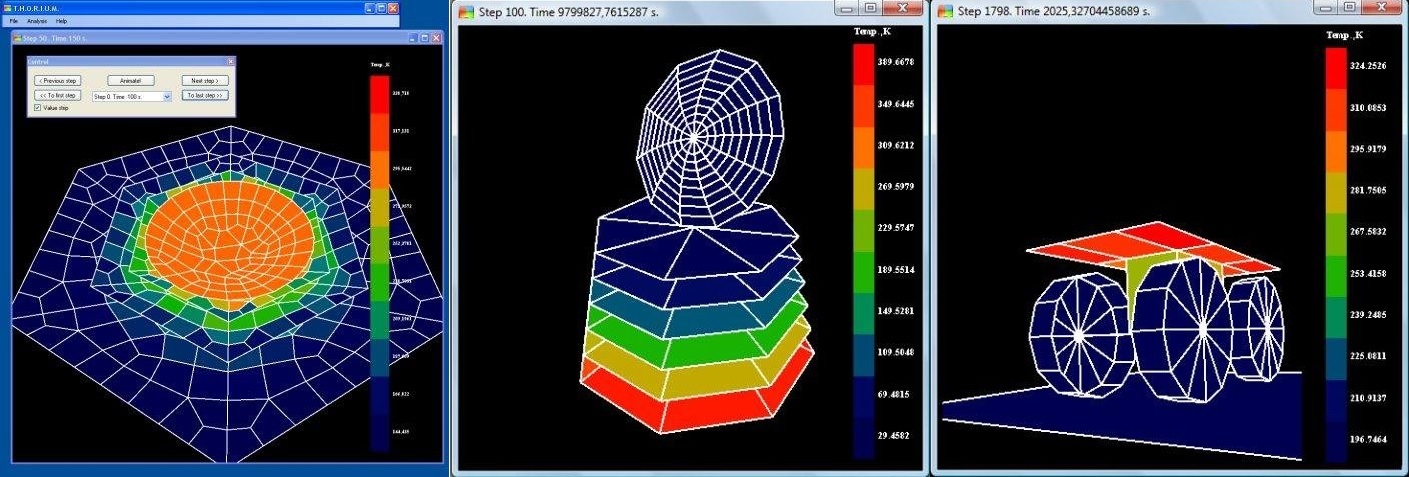
До этого, Саша писал дисер — «Метод решения задачи лучистого теплообмена без матрицы угловых коэффициентов» (диссертация, автореферат). Код тут. (он на VB.NET, тормозной, но работает и даже есть документация)
Космоинженеры используют метод Монте-Карло и до них вдруг дошло, судя по всему, система дифференциальных уравнений является стохастической, раз их часть получается методом случайных испытаний.
Парни хотят написать алгоритм, который решал бы систему дифуров как можно быстрее, и поэтому им нужна консультация математика-специалиста в области численного решения стохастических дифференциальных уравнений.
Основную сложность ребята вроде решили, построив массивно-параллельный алгоритм расчета хода излучения с методом Монте-Карло на CUDA. Теперь они хотят использовать для интегрирования своей системы, а она большой размерности, порядка 100 тыс. неизвестных, и жесткая, подходящий метод интегрирования по времени. Обычные явные методы требуют слишком мелкого шага по времени, а неявные требуют много раз вычислять правую часть, что ресурсозатратно.
Поэтому и нужно найти или построить такой метод интегрирования, который подходил бы для такого сочетания требований и позволял бы считать быстро.
Читать полностью »