Цель данной статьи – поднять вопросы распараллеливания кода программы для численного моделирования методом молекулярной динамики (МД) с помощью технологии CUDA. Зачем это вообще нужно, ведь уже существуют программные пакеты по МД, работающие в том числе и на CUDA? Дело в том, что я развиваю свою собственную концепцию «непостоянного поля сил» (non-constant force field), которая не реализована в существующих МД-программах.
Переделывать чужой код под эти нужды – довольно неблагодарное занятие, поэтому я взялся перенести уже написанный свой последовательный код и заодно поделится некоторыми размышлениями. Кроме того, это ответ на часто мелькающий здесь комментарий к статьям по CUDA, вроде этого .
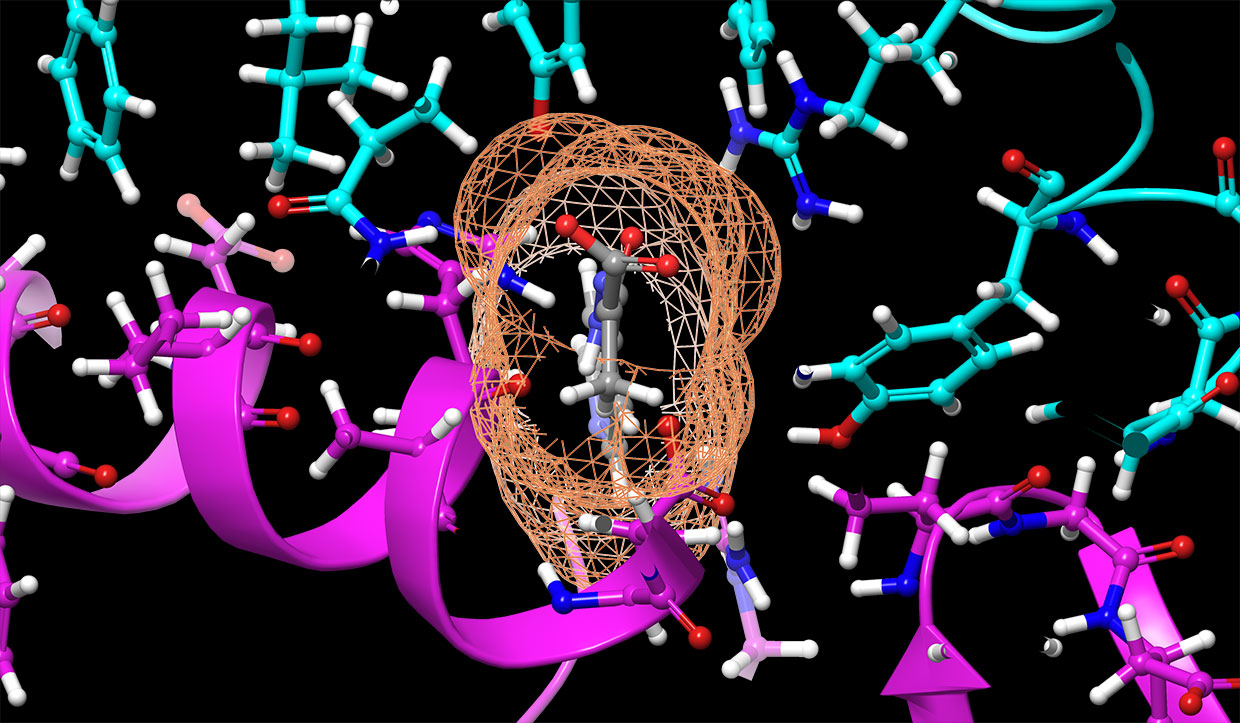
Итак, что же такое молекулярная динамика? На Хабре уже есть несколько постов на эту тему, например здесь или вот здесь. Кратко, МД – это метод, позволяющий моделировать движение множества частиц (в том числе атомов, ионов, молекул) и рассчитывать коллективные свойства системы, зависящие от этого движения. Как это работает? Допустим для множества из N частиц заданы некоторые начальные координаты, скорости, массы и (главное!) законы взаимодействия между ними. Изменяем координаты согласно скоростям. На основе законов взаимодействия вычисляем силы, действующие между частицами. Раз знаем силу и массу – знаем ускорение. Поправляем скорость с учетом ускорения. И снова переходим к изменению координат. И так повторяем тысячи раз, пока не надоест не наберем достаточную статистику.
Читать полностью »