В этой заметке я не собираюсь причитать как старая бабка «всё разворовали, упыри!!», потому что не интересуюсь кто это делает и делает ли. Не интересует меня и излюбленная темка автомобилистов «задолбали эти ямки и колдобинки!», лично мне не на чем их объезжать: в вопросах выбора транспортных средств я предпочитаю ретранслировать мнение Андрея Рубанова из его книги «Йод» (э маст хэв ящитаю), в мирное же время есть велосипед и автобус. У меня нет и претензий к нашим ремонтным службам, кладущим, как о том пишут в этих ваших интернетиках, битумную смесь на дождик и снежок вопреки мнению этих самых интернетов. Я простой пешеход, и пока ещё меня устраивает сложившееся положение вещей.
Кстати, я и не математик вовсе, а всего-то студент а-ля математик-прикладник. Если кто не в курсе, это такие чуваки и чувихи (да простит меня офисный планктон), по долгу своих профессий вынужденные перерабатывать в алгоритмы математические формулы именитых и широко известных в узких кругах теоретиков. Эти наколенкеписаные алгоритмы в свою очередь работают сначала в прикладных исследованиях, а затем идут в прикладной софт, если вдруг по велению судьбы рынок возжелает закупить наработки математика-прикладника, погрязшего по уши в фортрано-матлабо-пропитоненных сорцах.
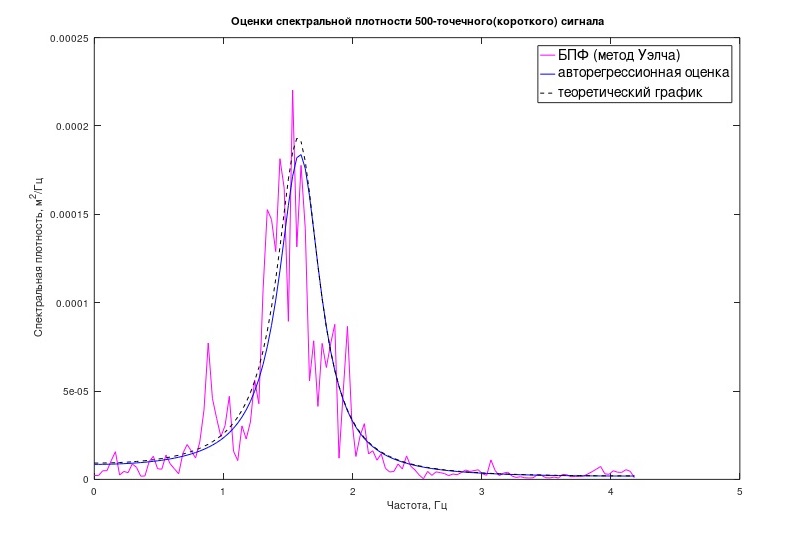
Так исторически повелось, что на студенческой скамье мне пришлось периодически решать задачи, за которые никакой другой более обеспеченный и, надо полагать, более разумный хомосапиенс не брался. И вот, по долгу своей студенческой стези познакомили меня с одной задачкой из области дорожно-строительных конструкций. Тема была «бесперспективняк». «О, чёт новенькое», — подумал я, и взялся за решение чисто в обмен на получение практических скиллов, бесплатно. Итоги работы меня немного удивили. Но обо всём по порядку, должным для гиктаймс стилем «научпоп для уставших за день сисадминов и начинающих лысеть погромиздов» ;)
Читать полностью »