В этой статье я расскажу об одной необычной формуле, которая позволяет взглянуть под новым углом на аффинные преобразования, а особенно на обратные задачи, которые возникают в связи с этими преобразованиями. Обратными я буду называть задачи, требующие вычисления обратной матрицы: нахождение преобразования по точкам, решение системы линейных уравнений, преобразование координат при смене базиса и т.д. Сразу оговорюсь, что в статье не будет ни фундаментальных открытий, ни уменьшения алгоритмической сложности — я просто покажу симметричную и легко запоминающуюся формулу, с помощью которой можно решить неожиданно много ходовых задач. Для любителей математической строгости есть более формализованное изложение здесь [1] (ориентированно на студентов) и небольшой задачник вот здесь [2].
Читать полностью »
Рубрика «барицентрические координаты»
Геометрия данных 6. Физика и математика
2017-11-03 в 11:07, admin, рубрики: барицентрические координаты, время, дзета-функция Римана, Дистанционные координаты, математика, простые числа, псевдоевклидово пространствоЭто заключительная статья серии о ди- и би-координатах. В размашистом и свободном стиле покажем, как введенные понятия можно использовать для исследования данных. Конкретно обратимся к теории чисел — это хорошее поле для демонстрации идей как математики, так и физики.
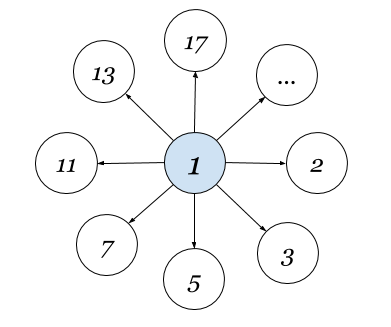
Физика — почему пространство-время псевдоевклидово?
Особенность дистанционных координат в том, что лежащее в их основе понятие дистанции (квадрата расстояния) между объектами играет ключевую роль в свойствах окружающего нас мира.
Читать полностью »
Геометрия данных 5. Преобразование базиса
2017-10-27 в 8:14, admin, рубрики: барицентрические координаты, граф, Дистанционные координаты, математика, матрица преобразованияПод преобразованием базиса системы координат понимается замена одного набора базовых вершин (реперов) на другой. По сравнению с обычной системой координат на векторах изменение системы координат на точечном базисе имеет особенности, связанные с тем, что базисы могут принадлежать разным пространствам.
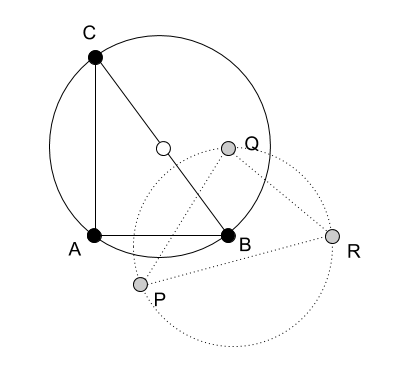
В предыдущей части было рассмотрено определение базиса низкой размерности в пространстве высокой размерности и показано, каким образом можно определять дистанции между вершинами, не принадлежащими пространству базиса. При замене базиса требование сохранения метрических свойств системы координат также является ключевым.
Читать полностью »
Геометрия данных 4. Пространство графа
2017-10-20 в 7:21, admin, рубрики: барицентрические координаты, граф, Дистанционные координаты, лапласиан, математика, матрица смежности, скалярное произведение, фундаментальная матрицаОсобенность координатных систем на точечном базисе (ди- и би-координат) состоит в том, что их можно использовать как в обычном геометрическом пространстве, так и в пространстве графа.
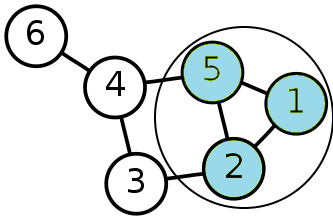
Пространство графа — это множество связанных между собой узлов (вершин графа). Каждый узел графа — это точка его пространства. В отличие от обычного геометрического пространства мерность пространства графа определяется количеством его узлов, — чем их больше, тем больше мерность.
Определение системы координат
Задачу построения системы координат (СК) на графе можно сформулировать следующим образом.
Читать полностью »
Геометрия данных 2. Ди- и би-координаты точек и векторов
2017-10-06 в 8:13, admin, рубрики: барицентрические координаты, граф, Дистанционные координаты, математика, симплексСтатья является продолжением серии о системах координат на точечном базисе. Базис представляет собой вершины симплекса или графа с известными значениями двух взаимных метрических тензоров — дистанционного (ДМТ) и лапласовского (ЛМТ). В первой статье описаны свойства данных тензоров. Здесь покажем, что представляют собой координаты точек.
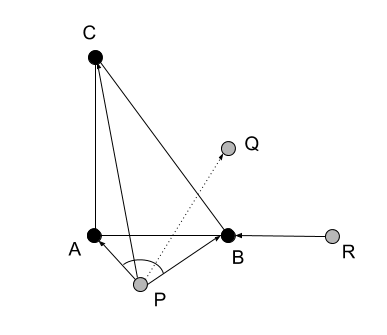
Дистанционные координаты
Для лапласовского метрического тензора (ЛМТ) координатами, описывающими точку в пространстве, являются дистанционные координаты. Данные координаты представляют собой объединение скалярной единицы и значений отрицательных полудистанций от точки до реперов — вершин базисного симплекса или графа. Для краткости будем именовать их ди-координатами.
Читать полностью »