Рубрика «Алгоритмы» - 72

в 12:55, , рубрики: minesweeper, Алгоритмы, геймплейная логика, логические игры, разработка игр, сапёр
Как решить «Сапёра» (и сделать его лучше) - 1

«Сапёр» (Minesweeper) — это простая игра с простыми правилами, однако некоторые её конфигурации создают любопытные трудности. В этой статье мы создадим солвер «Сапёра» с увеличивающейся сложностью, и поразмышляем над тем, как меняется динамика игры при постепенном повышении уровня помощи. В конце мы разработаем новый вариант игры с гораздо более интересным геймплеем.

Локальные рассуждения: ноль соседних мин

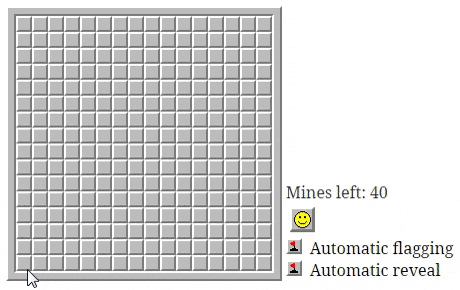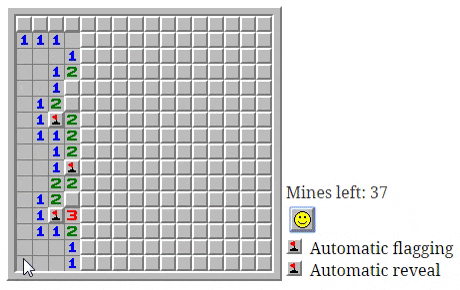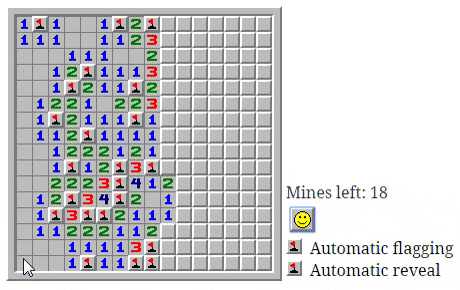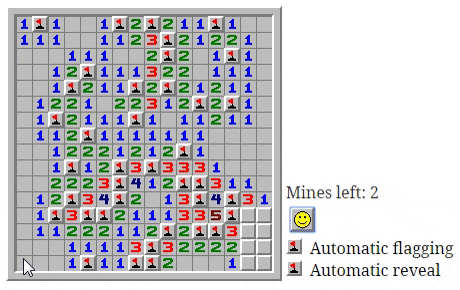
В оригинальной игре используется один автоматический механизм: когда игрок открывает клетку, рядом с которой нет мин, движок игры открывает все соседние клетки. Это ничем не угрожает игре, поэтому можно спокойно позволить компьютеру это сделать, а сама ситуация сразу же понятна игроку и никак не мешает геймплею.

Такое рассуждение совершенно локально: для принятия решения о следующем действии учитывается информация только одной клетки.

Сложно придумать ситуацию, в которой игра стала бы хуже без этой автоматической помощи. Попробуйте сыграть в такую игру, чтобы получить представление о том, как она проходит без автоматического открытия клеток [в оригинале статьи все примеры интерактивны]Читать полностью »

в 17:14, , рубрики: data mining, Алгоритмы, вейвлеты, математика, нестационарный процесс, спектральная плотность

Общеизвестно, что большинство временных рядов, с которыми приходится иметь дело исследователю, являются нестационарными, и их анализ ощутимо сложнее, чем изучение стационарных процессов. Поскольку интерес к вейвлетам, похоже, пошел на убыль, полезно обсудить некоторые иные «нестационарные» инструменты, пригодные, в первую очередь, для оценки мгновенных частот, а также для оценки мгновенных спектров.

В первую очередь есть смысл вспомнить об «аналитическом сигнале». Ниже «An-моделью» именуются как раз нахождение мгновенных импеданса и мощности тестового сигнала после достройки его мнимой частью (сдвинутой по фазе на π/2).

Но не всегда есть возможность возиться с преобразованием Гилберта. Ранее уже упоминалось об авторегрессионном способе спектрального оценивания, пригодном для работы с короткими последовательностями. Под «AR-моделью» здесь будет подразумеваться исследование коротких (из 5 сэмплов) перекрывающихся фрагментов исходного сигнала с целью определения коэффициентов авторегрессии 2-го порядка, нахождение по ним «полюсов» модели и т.д.

imageЧитать полностью »

в 9:18, , рубрики: .net, C#, CV, levenstein, ocr, parser, Алгоритмы, обработка изображений, Программирование

Умный парсер числа, записанного прописью - 1

Пролог

Добрый день, уважаемые читатели. В данной статье я расскажу о том, как распарсить число, записанное прописью на русском языке.

Умным данный парсер делает возможность извлечения чисел из текста с ошибками, допущенными в результате некорректного ввода или в результате оптического распознавания текста из изображения (OCR).

Для ленивых:
Ссылка на проект github: ссылка.

Читать полностью »

в 17:10, , рубрики: Алгоритмы, Программирование, сортировка

Как нетрудно догадаться, я знаю ответ на этот вопрос, но, поскольку моя статья с описанием алгоритма сортировки «воронкой» была здесь встречена, мягко говоря, нервозно, я решил провести-таки тестирование «по образу и подобию» тех, которые обычно проводятся — в основном, конечно, по материалам статей, представленных здесь же, на Хабре.

В Интернете не представлены трудные массивы для алгоритмов сортировки (мне, во всяком случае, их найти не удалось), а многочисленные «сравнительные анализы» алгоритмов на массивах в несколько сотен или тысяч элементов, просто смешны, а потому я решил прогнать «воронкой» те массивы, на которых проводились исследования с количеством элементов, по крайней мере, 10^5 и более.

Сначала небольшой обзор того, что пишут про алгоритмы сортировки с моими комментариями:
Читать полностью »

в 6:47, , рубрики: Алгоритмы, биржевая торговля, Блог компании Московская Биржа, высокая производительность, резервное копирование, торгово-клиринговая систем

Эволюция архитектуры торгово-клиринговой системы Московской биржи. Часть 2 - 1

Это продолжение длинного рассказа о нашем тернистом пути к созданию мощной, высоконагруженной системы, обеспечивающей работу Биржи. Первая часть тут.
Читать полностью »

в 17:39, , рубрики: griat-csp, Matlab, MIMO, Алгоритмы, математика, сотовая связь

Чтобы передать сообщение от базовой станции мобильному устройству (и наоборот), электромагнитной волне приходится преодолевать значительное количество препон: отражения, преломления, рассеивания, затенения, доплеровские смещения частот и так далее. Во-первых, все эти воздействия принято называть мультипликативными (от англ. multiplication — умножение) — по математической модели таких воздействий. А, во-вторых, можно собрать под общим термином замирания (fading).

От стандарта к стандарту, от поколения к поколению, от технологии к технологии ученые и инженеры бились и бьются над проблемой нивелирования этих замираний (fading mitigation).

И некоторые решения нашли широкое распространение. Скажем больше: почти все из них, так или иначе, связаны с понятием разнесения (diversity).

MIMO spatial diversity: Аламоути, DET и прочее пространственное разнесение - 1Читать полностью »

в 15:20, , рубрики: алгоритм быстрого умножения, алгоритм Карацубы, Алгоритмы, Искусство программирования, кнут, Колмогоров, математика, Читальный зал

Дональд Кнут — учёный в области информатики, который настолько заботится о правильности своих книг, что предлагает один шестнадцатеричный доллар ($2,56, 0x$1,00) за любую найденную «ошибку», где ошибкой считается всё, что «технически, исторически, типографически или политически неправильно». Я очень хотел получить чек от Кнута, поэтому решил поискать ошибки в его выдающемся труде «Искусство программирования» (TAOCP). Удалось найти три. Верный слову, Кнут прислал чек на 0x$3,00.

Я получил от Кнута чек на 0x$3,00 - 1

Как видите, это не настоящий чек. Раньше Кнут отправлял реальные чеки, но прекратил в 2008 году из-за безудержного мошенничества. Теперь он рассылает «личные депозитные сертификаты» в банке Сан-Серрифф (BoSS). Он говорит, что готов выслать реальные деньги в случае необходимости, но, похоже, это слишком хлопотно.
Читать полностью »

в 9:20, , рубрики: puzzle game, Алгоритмы, головоломки, Дизайн игр, логические игры, процедурная генерация, разработка игр

В этом посте описывается генератор уровней для моей игры-головоломки Linjat. Пост можно читать и без подготовки, но он легче усвоится, если сыграть в несколько уровней. Исходный код я выложил на github; всё обсуждаемое в статье находится в файле src/main.cc.

Примерный план поста:

  • Linjat — это логическая игра, в которой нужно закрыть все числа и точки в сетке линиями.
  • Головоломки процедурно генерируются при помощи комбинации из солвера, генератора и оптимизатора.
  • Солвер пытается решить головоломки так, как это делал бы человек, и присваивает каждой головоломке оценку интересности.
  • Генератор головоломок создан таким образом, чтобы можно было с лёгкостью менять одну часть головоломки (числа) и при этом все остальные части (точки) менялись таким образом, чтобы головоломка оставалась решаемой.
  • Оптимизатор головоломок многократно решает уровни и генерирует новые вариации из наиболее интересных, найденных на текущий момент.

Правила

Чтобы понять, как работает генератор уровней, нужно, к сожалению, разобраться с правилами игры. К счастью, они очень просты. Головоломка состоит из сетки, содержащей пустые квадраты, числа и точки. Пример:

Создание процедурного генератора головоломок - 1

Цель игрока — прочертить вертикальную или горизонтальную линию через каждое из чисел при соблюдении трёх условий:

  • Линия, идущая через число, должна иметь ту же длину, что и число.
  • Линии не могут пересекаться.
  • Все точки необходимо закрыть линиями.

Пример решения:

Создание процедурного генератора головоломок - 2

Ура! Дизайн игры готов, UI реализован, и теперь единственное, что осталось — найти несколько сотен хороших головоломок. А для подобных игр обычно не имеет смысла пытаться создавать такие головоломки вручную. Это работа для компьютера.
Читать полностью »

в 8:39, , рубрики: Алгоритмы, Блог компании FunCorp, обработка изображений, сравнение изображений

Поиск похожих изображений, разбор одного алгоритма - 1

Пришлось мне недавно решать задачку по оптимизации поиска дубликатов изображений.

Существующее решение работает на довольно известной библиотеке, написанной на Python, — Image Match, основанной на работе «AN IMAGE SIGNATURE FOR ANY KIND OF IMAGE» за авторством H. Chi Wong, Marshall Bern и David Goldberg.

По ряду причин было принято решение переписать всё на Kotlin, заодно отказавшись от хранения и поиска в ElasticSearch, который требует заметно больше ресурсов, как железных, так и человеческих на поддержку и администрирование, в пользу поиска в локальном in-memory кэше.

Для понимания того, как оно работает, пришлось с головой погружаться в «эталонный» код на Python, так как оригинальная работа порой не совсем очевидна, а в паре мест заставляет вспомнить мем «как нарисовать сову». Собственно, результатами этого изучения я и хочу поделиться, заодно рассказав про некоторые оптимизации, как по объёму данных, так и по скорости поиска. Может, кому пригодится.
Читать полностью »

в 15:26, , рубрики: Алгоритмы, ассимптотика, математика, решето Эратосфена, сложность алгоритма

В комментариях к одному из прошлых постов о решете Эратосфена был упомянут этот короткий алгоритм из Википедии:

Алгоритм 1:

1: для i := 2, 3, 4, ..., до n: 
2:  если lp[i] = 0:
3:       lp[i] := i
4:       pr[] += {i}
5:   для p из pr пока p ≤ lp[i] и p*i ≤ n:
6:       lp[p*i] := p
Результат:
 lp - минимальный простой делитель для кажого числа до n
 pr - список всех простых до n.

Алгоритм простой, но не всем он показался очевидным. Главная же проблема в том, что на Википедии нет доказательства, а ссылка на первоисточник (pdf) содержит довольно сильно отличающийся от приведенного выше алгоритм.

В этом посте я попытаюсь, надеюсь, доступно доказать, что этот алгоритм не только работает, но и делает это за линейную сложность.
Читать полностью »

1...1020...717273...8090...315
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js