Добрый день! Долго думал, писать пост или нет. Но буквально на днях появился утвержденный календарь ЧР по футболу 2013/2014, и вот под впечатлением сие текст…
Что мы видим, взглянув на расписание игр.
Тур 16: 2 ноября Краснодар-Кубань и Зенит — Амкар… Навскидку в Краснодаре +10, в СПб -5.
Тур 17: 9 ноября Урал-Ростов: в Екатеринбурге -10, в Ростове — на –Дону +10, Рубин – Краснодар, аналогично…
Также и 23, 30 ноября, 7 декабря, 8 марта, 15 марта, прогресс шагает семимильными шагами, но обходит руководителей российского футбола стороной… В тоже время в мае, июле, августе многие «северные» команды приезжают в гости на юг, в самую жару, для того чтобы получать «солнечные удары»…?! «Такой хоккей нам не нужен!»
Читать полностью »
Рубрика «алгоритм» - 11
Российский футбол на «плюсе». А при плюсе? Или такой футбол нам не нужен: ч.1 теоретическая
2013-06-20 в 9:23, admin, рубрики: алгоритм, Алгоритмы, Проектирование и рефакторинг, спорт, управление проектами, метки: алгоритм, спортАвтоматическое приглашение друзей в сообщество (Odnoklassniki.ru)
2013-05-21 в 18:08, admin, рубрики: алгоритм, Алгоритмы, одноклассники, сообщество, социальные сети, метки: алгоритм, одноклассники, сообщество, социальные сетиКаждый, кому приходилось работать с социальной сетью «Одноклассники» знает, что разобраться в ней — та ещё задача. Поэтому я решил рассказать, как можно программно приглашать друзей в сообщество, поскольку в Интернете об этом информации практически нет.
Для работы нам необходима учётная запись на Одноклассниках и cURL (не обязательно, но с его помощью отправлять GET и POST запросы значительно проще).
Читать полностью »
Тщетные попытки победить лотерею
2013-05-14 в 9:35, admin, рубрики: алгоритм, Алгоритмы, игра, искусственный интеллект, лотерея, математика, теория вероятностей, метки: алгоритм, игра, лотерея, теория вероятностей Представим воображаемый хитрого дядю, который хочет обмануть и заработать деньги на «лопухах». Назовем его Геннадий Обмануев.
В самый обычный вторник, Геннадию Обмануеву вдруг пришла гениальная идея: создать лотерею, в которой каждый игрок может сам указывать свой шанс на победу и, следовательно, множитель выигрыша и играть на выставленных им правилах! Для того, чтобы всегда оставаться в плюсе, Геннадий в конце каждой удачной игры берет символическую плату в 5% от выигрыша.
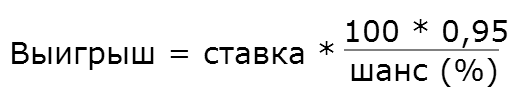
*если кратко об игре
Как и в случае с казино, чем дольше игрок играет в такую игру — тем более вероятно, что он, в конце концов, проиграет. Но неужели нельзя обмануть хитрого дядю, придумав чудесную тактику, благодаря которой можно увеличить свои шансы на победу?
Читать полностью »
Программная расстановка коэффициентов в химических уравнениях
2013-04-15 в 12:56, admin, рубрики: алгоритм, Алгоритмы, Песочница, Программирование, химия, метки: алгоритм, Программирование, химияВведение
Все, кто когда-нибудь изучал химию, знают, что это наука сложная и в многих моментах не совсем понятная. Например, у учеников средних и старших классов часто возникают проблемы с решением химических задач и уравнений. Поэтому они часто ищут ответ на задание с помощью химических калькуляторов. Но большинство программ этого класса нельзя назвать калькулятором — они не считают, а только проверяют результат в базе данных. Этот способ имеет очень большой недостаток — программа не выдаст результат, если уравнения реакции не будет в базе. Поэтому есть необходимость использовать алгоритм, который даст возможность находить коэффициенты программно. И такой алгоритм существует.Читать полностью »
Проблема четырех красок. Решение
2013-02-10 в 20:58, admin, рубрики: алгоритм, доказательство, задача, математика, Песочница, метки: алгоритм, доказательство, задача Доброго времени суток, Хабровчане!
В последнее время проблемы века стали очень популярными. Ими интересуется каждый себя уважающий математик. Сегодня Вашему вниманию хочу представить одну из проблем века, а именно — Проблема четырех красок и ее решение.
Проблема четырёх красок предложенна в 1852 году Фрэнсисом Гутри
Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Стоит отметить две необходимые характеристики этой карты:
- Граница между любыми двумя областями является непрерывной линией.
- Каждая область является односвязной.
Данная проблема изначально легка и ее решение приходит на ум почти сразу, но нет доказательства, а именно — алгоритма, по которому можно было бы раскрасить любую карту.

Единственным принятым доказательством, является выведенное из идей Альфреда Кэмпе в 1880 году (его изначальное доказательство увидело свет в 1879 году[1]), что любую карту можно раскрасить в 5 цветов.
Почти сорок лет назад, в 1976 году, в Иллинойском университете, Кеннет Аппель и Вольфганг Хакен предоставили доказательство. В качестве доказателства послужила компьютерная симуляция, которая перебирала все возможные конфигурации карт и выявила минимальное количество цветов равных четырем. Алгоритм симуляции пытались многократно упростить, чтобы проверить доказательство, но к сожелению, безуспешно. Эти события вызвали сомнения у многих математиков, тем более, что описание симуляции занимало аж 741 страницу.
Читать полностью »
Жеребьевка — нажатием кнопки
2013-01-29 в 16:11, admin, рубрики: алгоритм, Алгоритмы, метки: c++, алгоритм Для решения одной, как я считаю, амбициозной задачи, связанной с проведением футбольного турнира, мне необходимо было использовать процедуру формирования соревновательных пар, т.е. провести жеребьевку. Но произвести ее нужно не обычным «человеческим» способом, а автоматизировано. Поискав готовые решения аналогичной задачи, нашел только формирование корзин участников при наличии сеянных и несеянных команд (Пример), что меня не устроило и не решало поставленной задачи. В итоге проанализировав процедуру обычной однокруговой жеребьевки, сформировал следующий алгоритм и условия:
Входные условия жеребьевки:
- Имеется N команд – участников.
- Каждая команда за первый круг сыграет N-1 матчей.
- Команда N ни в каком из туров не может сыграть сама с собой.
- В каждом туре соперники образуют уникальные, не повторяющиеся ранее пары.
- Если в каком-то из туров команда N играет с командой M, то соответственно в этом же туре команда M играет с командой N.
Сопоставив процесс формирования случайных пар соперников процедуре заполнения двумерного массива DrawTable[i, j] случайными величинами, получил следующее (язык C#, .Net 4.0):
Читать полностью »
Иерархический поиск пути
2013-01-22 в 19:08, admin, рубрики: game development, HPA*, rpg, RTS, алгоритм, Алгоритмы, поиск пути, Программирование, метки: HPA*, rpg, RTS, алгоритм, поиск пути 
Для разработки небольшой компьютерной игры зачастую применяются базовые алгоритмы поиска пути (алгоритм Дейкстры, А*), которых вполне достаточно для игрового поля не слишком больших размеров. Однако как же решить задачу о поиске пути на громадных игровых пространствах в играх жанра RTS или RPG? Ведь в виду значительного потребления памяти и ресурсов процессора базовые алгоритмы не подходят. О решении этой проблемы (а также нескольких других) и пойдет речь дальше в статье.
Читать полностью »
Симуляция жизни в системе Darwinbots. II. Симуляция и простейший бот
2013-01-15 в 16:06, admin, рубрики: алгоритм, Алгоритмы, Биотехнологии, выживание, генетика, генетический алгоритм, естественный отбор, Программирование, симуляция, метки: алгоритм, выживание, генетика, генетический алгоритм, естественный отбор, Программирование, симуляция 
Приветствую вас еще раз, дорогие читатели!
Эта статья выкладывается в разгар сессии, так что я могу пропасть из комментариев.
1. Первое знакомство
2. Симуляция и простейший бот
Сегодня разберёмся с настройками симуляции и посмотрим на простейшего бота (или робота, как вам будет удобно). Нет, я не буду досконально рассматривать интерфейс программы – это будет вашим домашним заданием:-) И да, само понятие «генетический алгоритм» четко расписано в Википедии, поэтому опустим это объяснение.
Читать полностью »
Квантовые вычисления, часть вторая
2013-01-10 в 12:17, admin, рубрики: алгоритм, Алгоритмы, квантовые вычисления, квантовый компьютер, ненормальное программирование, Программирование, метки: алгоритм, квантовые вычисления, квантовый, квантовый компьютерСказал как-то раз Евклид, что параллельные линии не пересекаются. И назвал он это пятым постулатом. Жалко, что не вторым.
В этой статье я бы хотел перейти от сферических котов Шредингера в резонаторах Гельмгольца к чему-то более практичному, тем более, что Хабр интересуют физические реализации и применение квантовых компьютеров.
Тут я решил рассказать про составные системы и описать алгоритм Дойча.
Симуляция жизни в системе Darwinbots. Часть первая
2013-01-04 в 10:53, admin, рубрики: алгоритм, Алгоритмы, Биотехнологии, выживание, генетика, генетический алгоритм, естественный отбор, Программирование, симуляция, метки: алгоритм, выживание, генетика, генетический алгоритм, естественный отбор, симуляция Привет!

Недавно сдал курсовую работу по генетическим алгоритмам в программе Darwinbots и решил, что это будет интересно сообществу. Тем более, что в данный момент сообщество проекта довольно мало. Статьи будут наполовину переводом документации, а наполовину своими исследованиями программы.
Читать полностью »
