[Прим. пер.: на Хабре уже был перевод этой статьи, но незавершённый примерно на четверть.]
Неправда.
Калькулятор должен показывать результат введённого математического выражения. А это намно-о-ого сложнее, чем кажется.
В этом посте я расскажу величайшую историю о разработке приложения-калькулятора.

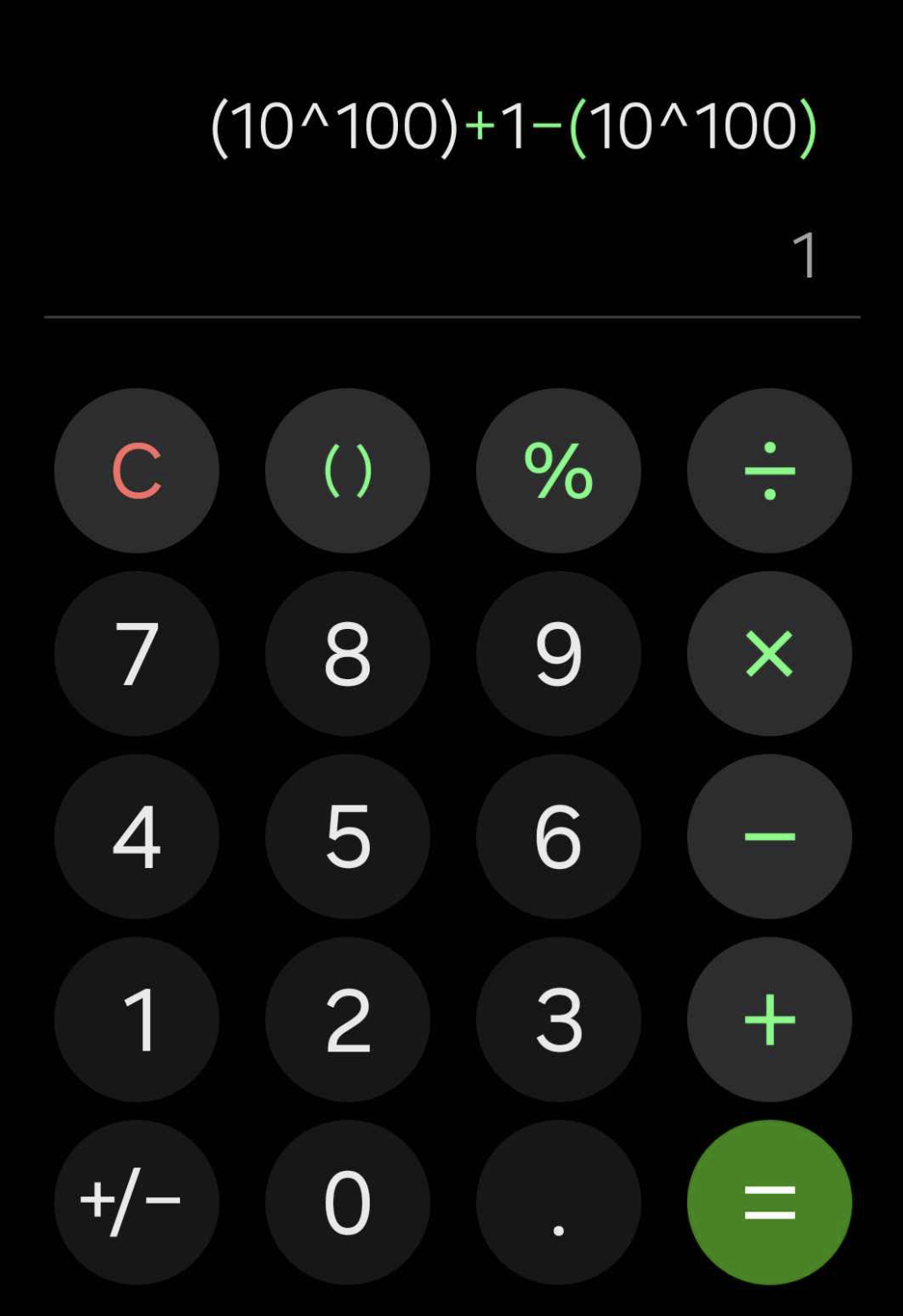
На изображении выше показан калькулятор из iOS.
Заметили что-нибудь?
Он посчитал неправильно.
(10100) + 1 − (10100) равно 1, а не 0.
Android считает правильно. А причина, по которой он это делает, абсолютно безумна.
Google нанял Ханса-Юргена Бёма, знаменитого созданием «сборщика мусора Бёма» (Boehm garbage collector). Компании нужен был элитный кодер, способный решить проблемы сборки мусора и параллельного программирования. Он возглавил проект по разработке семантики разделяемых переменных C++. Но потом Google дал ему задачу, которую невозможно решить: создание приложения-калькулятора.

Наверно, даже для него это было сложно.
Задача калькулятора — давать правильные ответы. Числа с плавающей запятой неточны — они не могут представить 0,3 или 10100. То есть создание калькулятора на основе чисел с плавающей запятой похоже на строительство дома на песке.
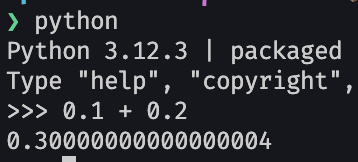
Наверно, это стоит объяснить подробнее: чтобы давать правильные ответы математических выражений, калькулятор должен обрабатывать числа.
Но почти никакие числа невозможно выразить в стандарте чисел с плавающей запятой IEEE.
Для получения точных ответов при даже самых простых операциях с такими числами требуется тщательно всё продумывать.
Некоторых проблем можно избежать, если пользоваться арифметикой с произвольной точностью (bignum-арифметикой).
Большинство числовых типов всегда имеют длину 2 или 4 байта. Но с bignum всё не так. Это безграничные целые числа, которые при необходимости разрастаются в памяти.
Это решает проблему с примером (10100) + 1 - (10100). Но bignum — это целые числа. А как же насчёт дробей?
Проблема дробей легко решается: достаточно использовать bignum для числителя и знаменателя. Реализация арифметических операций с такими типами тривиальна и всегда даёт точные ответы.
На этом многие бы начали праздновать победу. Но Бёма это не удовлетворило.

Математика — это далеко не только одни дроби. Как насчёт π или √2? Калькулятор, построенный на основе дробей с произвольной точностью, не сможет вычислить длину окружности, потому что π нельзя выразить в виде дроби.
Если калькулятор не способен справиться с математикой девятого класса школы, то кому он нужен?
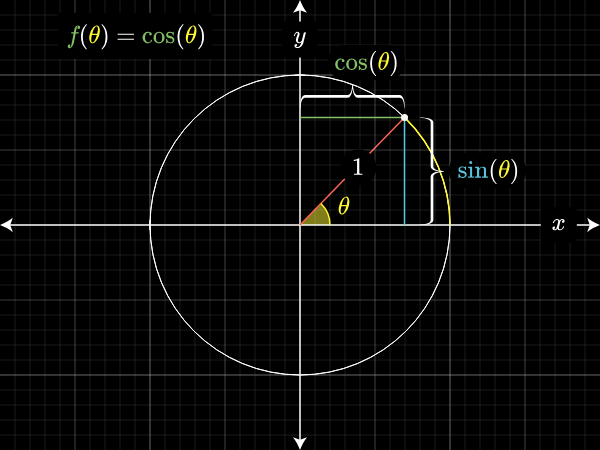
Приблизиться к решению Бёму позволила алгебраическая арифметика.
Забудьте о представлении чисел в виде числителей и знаменателей.
Можно представить их в виде степенного уравнения.
Для √2 это будет x² - 2 = 0. (Плюс необходимо хранить информацию, что нам нужен только положительный корень.)
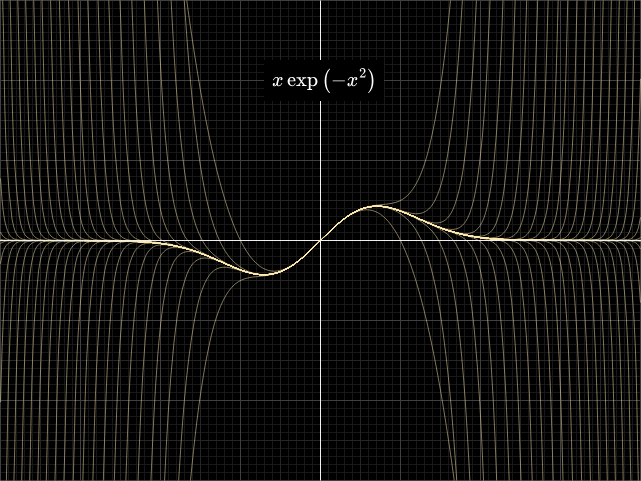
Теперь математические операции реализовать будет сложнее:
-
Для сложения нужно создать новый многочлен, корень которого является суммой слагаемых
-
Для умножения нужно использовать композицию многочленов и результанты
И знаете что? Бёму всё равно этого было недостаточно. Это сработает только с алгебраическими числами, но не с π. Поэтому Бёму не оставалось ничего другого, кроме как ещё глубже закапываться в проблему.
Мы начали с целых чисел (bignum), перешли к рациональным числам, затем к алгебраическим. Что дальше?
Конструктивные вещественные числа.
Так Бём начал исследовать «рекурсивную вещественную арифметику» (recursive real arithmetic, RRA). Для выражения и указанной точности RRA позволяет получить ответ как минимум с этой точностью.
Посмотрите на обложку этого старого учебника. Видите, что линейки становятся всё меньше и меньше?

Конструктивные вещественные числа — это такие числа, которые можно вычислять со всё большей и большей точностью.
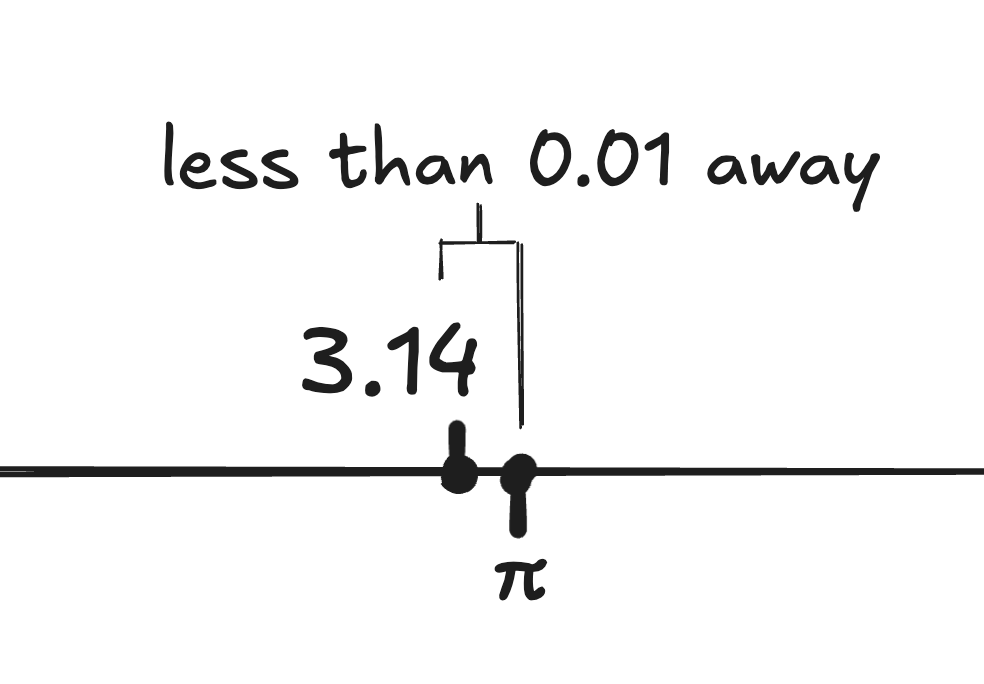
Мы никогда не сможем перечислить все цифры после запятой в π. Но если я спрошу рациональное число на расстоянии не больше 0,01 от π, то вы назовёте 3,14.
π находится в пределах 0,01 от 3,14, так что это правильный ответ.
Допустим теперь, что я спрошу число на расстоянии 0,01 от 2π.
Вы знаете, как получать цифры π после запятой (3,14159...).
Можно умножить их на 2. Но сколько разрядов нужно взять, чтобы ответ точно был в окрестности 0,01 от 2π?
Умножение числа на 2 удваивает погрешность. Я спросил число в окрестности 0,01 от 2π, поэтому нам нужна аппроксимация π в окрестностях 0,005.
Допустим, вы получили 3,141, что и в самом деле находится на расстоянии меньше 0,005 от π. Умножим его на 2 и готово!
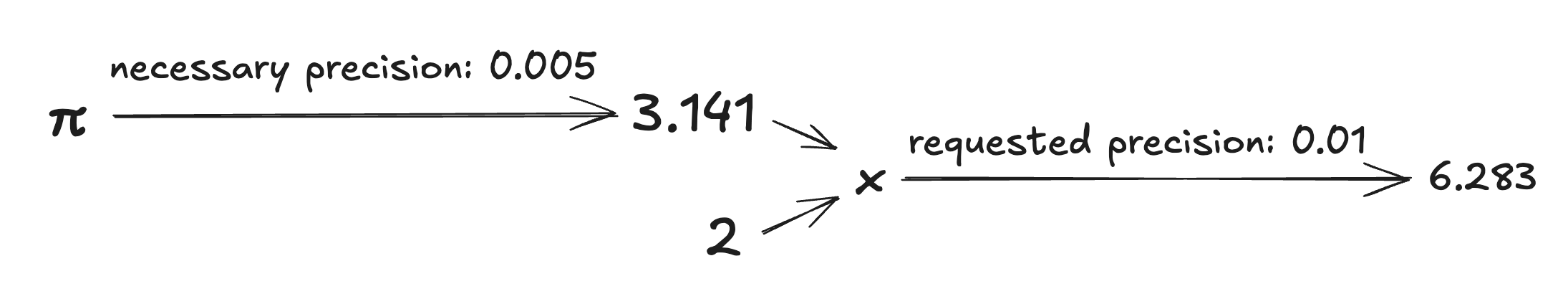
Так и работает RRA.
Каждое число в RRA представлено в виде функции, получающей рациональное число и возвращающей рациональное число.
Получаемое им рациональное число — это требуемый допуск.
Возвращаемое рациональное число гарантированно находится в пределах допуска представляемого им вещественного числа.

Благодаря этому RRA легко использовать. Вы говорите, насколько точным должен быть ответ, а она рекурсивно определяет необходимую точность во всех промежуточных вычислениях.
Она без проблем может работать с выражениями, где есть π или √2. А калькулятору без этого не обойтись.
Вы, наверно, думаете, что Бём на этом остановился?
В качестве «точности вывода» он указал количество разрядов калькулятора, ведь так?
Тогда все отображаемые на калькуляторе разряды будут правильными, а значит, теперь он всегда будет показывать правильный ответ! Ведь так?
Не будем торопиться. Когда пользователь вводит «1-1», то ответом должен быть 0, поэтому мы хотим показать «0».
Однако RRA только сообщит нам, что «1-1 находится в пределах погрешности округления 0,0000000000000»
Если показывать на экране 0,0000000000000, когда ответ равен 0, то это будет ужасно с точки зрения UX.
Бём снова вернулся к анализу. Наверно, он уже был сильно озадачен. По сравнению с этой проблемой его «эффективно использующая пространство консервативная сборка мусора» казалась детской забавой.
В одиночку он бы не справился, поэтому призвал на помощь своих коллег, например Роберта Картрайта и Вернона Ли

Мы можем проверить два RRA-числа на неравенство. Можно вычислять их со всё большей и большей точностью, пока мы не увидим, что они различаются.
Но если числа равны, то мы бесконечно будем вычислять их со всё большей точностью. Этот процесс не имеет завершения, это алгоритмически неразрешимая задача.
Вспомним, что если калькулятор покажет 0 как ответ выражения e-10000, то это будет неверно. Он должен показать 0,00000... и позволить вам проскроллить все нули, чтобы найти, где появляются другие значения. Но он ДОЛЖЕН показывать 0 при вводе sin(π), потому что sin(π) точно равен 0. RRA никак не позволяет нам определить, что sin(π) точно равен 0. Или можно просто не давать ответ, как это делает калькулятор iOS:

То есть задачу отображения точного ответа невозможно решить при помощи конструктивных вещественных чисел. Но потом Бёма и его коллег осенило: им не нужно работать с конструктивными вещественными числами. Достаточно работать только с числами, которые можно выразить при помощи имеющихся в калькуляторе операций
А именно:
-
Четырьмя базовыми арифметическими операциями и квадратными корнями.
-
Тригонометрическими функциями sin, cos и tan, а также обратными им функциями.
-
Степенными функциями и (натуральными) логарифмами
Это гораздо меньшее множество чисел, чем все конструктивные вещественные. И оказалось, что другие люди уже исследовали именно эту задачу. Их звали Дэн Ричардсон и Джон Фитч. Они решили её в 1994 году.

Их решение было абсолютно корректным, за исключением случаев, когда одно из чисел оказывается контрпримером гипотезы Шануэля.
Но на самом деле такого никогда не случится.
Гипотеза Шануэля — одна из важнейших в теории чисел, и пока никто не нашёл для неё контрпримера.
Похоже на идеальное решение. Но есть лишь одна проблема: оно слишком медленное.
1 не равно 1 - e(-e^1000). Но чтобы это определил алгоритм Ричардсона и Фитча, потребуется больше этапов, чем атомов во Вселенной. Нужно было придумать что-то более быстрое. Изначально Бём с коллегами ставили задачу определения равенства двух конструктивных вещественных чисел. А её решить невозможно. Они упростили её и приблизились к решению, ограничив способы конструирования чисел. Это сделало задачу решаемой, но медленно.
Можно ли ещё раз упростить её?
Они поняли, что нет ничего особо страшного в том, чтобы показывать «0,000000...» в случае, когда ответ равен 0, хоть это и неидеальный UX. Нельзя лишь показывать «0» в случае, когда ответ 0,0000001.
Может быть, есть какой-то более быстрый консервативный алгоритм?
И они придумали нечто поистине великолепное.
RRA даёт нам всю мощь конструктивных вещественных чисел, но имеет один недостаток: с её помощью невозможно получить точные ответы. Рациональная арифметика даёт точные ответы, но не может выразить π. Можно ли объединить их сильные стороны?
Разработчики осознали, что если пользователь просто вводит 6 * 9 или 8 / 3, то полная мощь RRA не требуется, достаточно рациональной арифметики. RRA нужна только в случаях, когда рациональных чисел недостаточно. Можно использовать её, когда в дело вступают числа наподобие π или √2, а в остальных случаях применять рациональные числа
Рациональные числа точны, но в них нельзя выразить π.
RRA-числа могут описывать числа наподобие π, но не могут быть точными.
Разработчики придумали такое решение: представлять каждое число как рациональное, умноженное на RRA-число. Но этого недостаточно. Как только в дело вступают RRA-числа, результат обязательно становится неточным.
Но даже в случае иррациональных чисел RRA иногда может быть излишней.
RRA представляет π в виде функции, способной возвращать рациональные числа, с произвольной точностью близкие к π. (Точно так же, как все RRA-числа представляются в виде функций)
Можно сказать: «Мне нужно число π с точностью 0,001», и RRA ответит: «это 3,141»

Иногда нам нужна RRA. Но на этот случай можно просто иметь особое представление π, которое мы будем особым образом использовать вместо её функции RRA. Мы называем это символьным представлением, поскольку это похоже на написание символа π вместо бесконечной последовательности чисел

Ага, дело пошло. А теперь давайте сделаем так не только для π. Очевидно, что нам нужно символьное представление вещественного числа 1. Но многие используемые нами иррациональные числа — это результат применения операции к рациональному аргументу. Для них можно тоже создать символьные представления.
Разработчики решили хранить символьные представления для √arg, eᵃʳᵍ, ln(arg), log₁₀(arg), sin(πarg), tan(πarg) и других функций (где arg — это какое-то рациональное число).
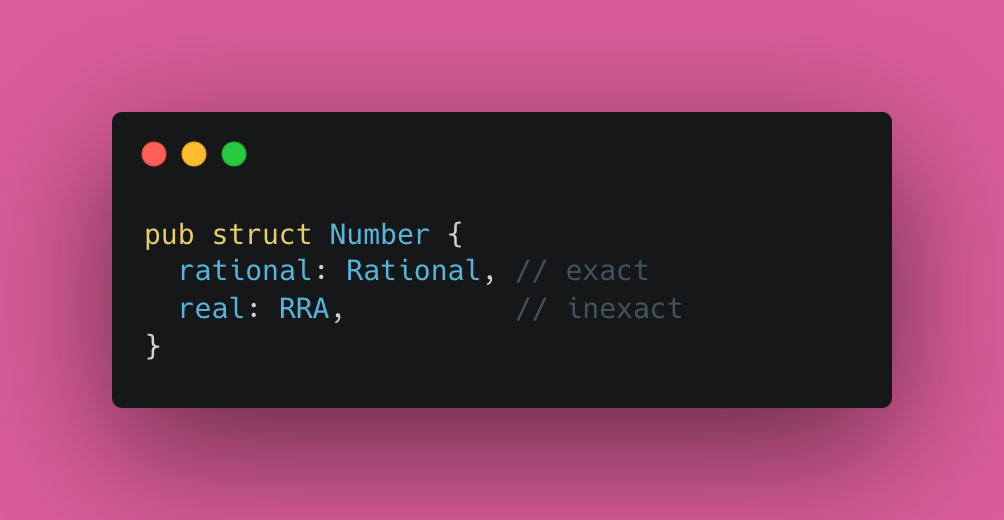
Итак, окончательное представление чисел выглядит так: рациональное, умноженное на вещественное, где вещественное — это или RRA-вещественное, или символьное вещественное.

Необходимо помнить, что фундаментальная проблема заключается в невозможности проверки RRA-чисел на равенство. Как только мы используем такое число, всё вычисление становится неточным, но иногда они необходимы. То есть Бёку и его коллегам достаточно было максимально избегать использования RRA-вещественных чисел!
Например, в (1 × π) + (3 × π) у нас, к счастью, есть символьные представления вещественных чисел. В обоих случаях это π.
Так как вещественные части одинаковы, мы можем выполнить суммирование, сложив рациональные части.
Если бы выражение имело вид (1 × π) + (3 × √2), то для вычислений мы бы использовали RRA.
Благодаря этому представлению разработчики добились баланса: все отображаемые на экране разряды всегда правильны и почти никогда не отображается больше разрядов, чем это необходимо.
«Система компьютерной алгебры» решила бы схожую задачу, но была бы гораздо медленнее и сложнее. Такая система настолько сложна, что её поддержкой на уровне продакшена способны заниматься очень немногие. А Бём и его коллеги придумали на 100% корректную систему, в 99% случаев обеспечивающую идеальный UX и ценой всего 1% сложности реализации.
Вот что называется настоящей разработкой ПО! Вам стоит прочитать статью Ханса-Юргена Бёма Towards an API for the Real Numbers.
Надеюсь, теперь вы больше будете ценить калькулятор в Android!
Автор: PatientZero






