Буквально пару часов назад Санкт-Петербурге завершился открытый чемпионат по программированию Яндекс.Алгоритм 2013. Состязания состояли из нескольких онлайн-раундов по 100 минут, за победу боролись более 3000 программистов из 84 стран. По результатам трёх отборочных раундов в финал вышли 25 лучших. Финал состоялся в Доме учёных имени Горького (дворец Великого князя Владимира Александровича)
Финалисты должны были решить шесть алгоритмических задач за 100 минут. Первое место занял недавний победитель ACM ICPC 2013 в составе команды НИУ ИТМО Геннадий Короткевич (tourist), который набрал меньше всего штрафного времени. Второе место досталось выпускнику НИУ ИТМО Евгению Капуну (eatmore). Третье место занял представитель Тайваня Ши Бисюнь.
В подготовке заданий для чемпионата участвовали специалисты из нескольких стран: России, Беларуси, Польши и Японии. Главными составителями задач стали разработчики минского офиса Яндекса (как и все сотрудники компании, к участию в состязаниях они не допускались). Мы попросили всех авторов разобрать задания, которые они подготовили для участников Яндекс.Алгоритма. Кстати, все задачи не удалось решить никому, лучший результат — три решённые задачи — показали только три участника.

Задача А. Сокращайте!
Автор задачи и разбора: Jakub Pachocki, Warsaw U
Имя входного файла: stdin
Имя выходного файла: stdout
Ограничение по времени: 8 секунд
Ограничение по памяти: 512 мегабайт
Обычно на командных соревнованиях по программированию, помимо полного названия вуза, задаётся сокращённое. На одном очень престижном соревновании команды планируют рассадить так, что из двух команд команда с лексикографически наименьшим сокращённым именем сидит ближе к буфету. С учётом этого тренеры каждого вуза стремятся сократить название вуза так, чтобы результат получился лексикографически минимальным.
Обозначим как слово непустую подстроку названия университета, которая состоит из букв, причём ни символ непосредственно перед этой подстрокой, ни символ сразу после неё буквами не являются. При сокращении названия вуза разрешается заменить любой суффикс некоторого слова знаком точки («.»).
При этом:
- Не разрешается заменять точкой всё слово.
- Если слово остаётся неизменным (то есть выбран пустой суффикс), точка не ставится.
Разрешается не сокращать название университета вообще, оставив его неизменным.
При сравнении названий все символы, не являющиеся латинскими буквами, удаляются, все заглавные латинские буквы заменяются соответствующими строчными и полученные в результате строки сравниваются между собой.
Формат входного файла. Первая строка входного файла содержит название университета. Название может содержать заглавные и строчные латинские буквы, пробелы, запятые («,») и дефисы («-»).
Гарантируется, что строка не начинается и не заканчивается пробелом и не содержит два последовательных пробела. Количество символов (включая пробелы) во входном файле не превосходит 106.
Формат выходного файла. Выведите лексикографически наименьшее сокращённое название университета. Запрещается изменять капитализацию букв и положение символов, не являющихся буквами, по сравнению с исходным названием. Если лексикографически наименьших
сокращений несколько, выведите любое.
| stdin | stdout |
| University of Warsaw | Uni. of W |
| Saint Petersburg National Research University of IT, Mechanics and Optics | Sain. Pe. Na. Research Uni. of I., M. and O. |
| University of Illinois at Urbana-Champaign | {Uni. of I. at U.-C |
| ,Carnegie--,--MelloN-,-, — University- | ,Ca.--,--MelloN-,-, — U.- |
| Udmurtian University | Udm. U. |
Note. «Uni. of W.» является лексикографически наименьшим сокращением для «University of Warsaw», так как строка «uniofw» является лексикографически меньшей, чем строки, соответствующие другим варинтам, к примеру, «uow», «uniofwa», «universityofwarsaw».
Решения задачи A.
После разбора ввода задача сводится к следующей:
Для n строк s1,… sn суммарной длины N найти такие их непустые префиксы p1,…, pn, что строка
p1p2… pn
является лексикографически наименьшей.
Предположим, что мы уже нашли pk+1,…, pn такие, что строка pk+1 pk+2...pn является лексикографически наименьшей. Заметим, что данный выбор pk+1, ..., pn оптимален при любом выборе p1, ..., pk. Это следует из того факта, что если для двух строк t и t' верно t < t', то wt < wt' для любой строки w.
Каким образом эффективно найти оптимальный префикс pk по заданным pk+1, ...., pn?
Положим t := pk+1p>k+2… pn. Нам нужно найти такой непустой префикс p строки sk, что строка pt является лексикографически минимальной.
Существует алгоритм, который позволяет эффективно сравнивать строки pt и p't, используя хэш:
- бинарным поиском находим наибольший общий префикс строк pt и p't;
- сравниваем символы, идущие сразу за этим префиксом.
При использовании рандомизированного хэша алгоритм работает за (log N) с весьма высокой вероятностью.
Для того чтобы найти pk, требуется провести |sk| — 1 таких сравнений, что даёт время (|sk| log N) для вычисления pk. Суммируя все sk, получаем время работы алгоритма (N log N).
Задача B. Анюта и «побитовое И»
Автор задачи и разбора — Роман Удовиченко.
Имя входного файла: stdin
Имя выходного файла: stdout
Ограничение по времени: 2 секунд
Ограничение по памяти: 512 мегабайт
Маленькая Анюта решила изучить битовые операции над числами. Сегодня она изучила операцию «побитовое И». Побитовое И — это бинарная операция, действие которой эквивалентно применению логического И к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов (в двоичном представлении допустимы лидирующие нули). Другими словами, если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0.
По удивительному стечению обстоятельств, как раз сегодня родители Анюты принесли с работы два набора чисел. Папа принёс с работы набор A, состоящий из P чисел, а мама — набор B, состоящий из M чисел. Все числа в наборах были целые, неотрицательные, а также не превосходящие 65535. Кроме того, числа в наборах были пронумерованы, начиная с 1.
Радостная Анюта тут же принялась применять изученную операцию к числам из этих наборов. Чтобы не обидеть никого из родителей, она применяла побитовое И к тем парам чисел, одно из которых было из папиного набора, а другое — из маминого.
Пока Анюта была увлечена вычислениями, родителям стало интересно, сколькими способами их дочка может получить некоторое число X? Количество различных способов можно посчитать, как количество различных пар (i, j) таких, что 1 ≤ i ≤ P, 1 ≤ j ≤ M, Ai AND Bj = X. Поскольку родители Анюты не менее любознательные, чем их дочка, они хотят найти искомое количество способов не только для одного числа X, а сразу для K чисел Xi. Помогите родителям!
Формат входного файла. В первой строке находятся три целых числа P, M и K (1 ≤ P, M, K ≤ 105), разделённые пробелами — количество чисел в наборе папы, количество чисел в наборе мамы, и количество чисел, интересующих родителей соответственно. Вторая строка содержит P чисел Ai, разделённых пробелами — набор чисел, который принёс папа. Третья строка содержит M чисел Bi, разделённых пробелами —- набор чисел, который принесла мама. Четвёртая строка содержит K чисел Xi, разделённых пробелами — набор чисел, для которых нужно посчитать искомое количество пар. Все числа в наборах A, B и X целые, неотрицательные и не превосходят 65535.
Формат выходного файла. Выведите K строк, содержащих по одному числу. Число в i-ой строке должно равняться количеству способов получить число Xi с помощью применения операции побитового И к числам из наборов A и B по правилам, описанным в условии.
Примеры
| stdin | stdout |
| 4 4 4 1 2 3 4 1 2 3 4 1 2 3 4 |
3 3 1 1 |
| 1 2 3 0 1 2 0 1 2 |
2 0 0 |
Решение задачи B
Даны два массива А и В, состоящие из целых неотрицательных чисел до 216. Также дан массив запросов Q, тоже содержащий числа до 216. Нужно для каждого запроса k сказать, сколько существует пар (i,j) таких, что Ai AND Bj = Qk.
Количество элементов в каждом массиве до 100к (хотя сразу понятно, что разных не более 216, но всё равно одинаковые надо обрабатывать, так пусть будут массивы до 100к).
Будем считать ответ сразу для для всех запросов.
Введем в рассмотрение следующие обозначения f(x, S) — множество элементов из последовательности S, которые содержат все биты из x и, возможно, еще какие-то (т.е. такие числа y, что x & y = x).
Заметим, если a ∈ f(x, A) и b ∈ f(x, B), то (a & b) & x = x, т.е. a & b содержит все те же биты, что и x, опять же, возможно, еще какие-то дополнительно.
Пусть g(x) — количество пар индексов (i, j) таких, что Ai & Bj = x, несложно видеть, что  . Таким образом, из всех возможных пар индексов мы вычитаем те, для которых Ai & Bj > x.
. Таким образом, из всех возможных пар индексов мы вычитаем те, для которых Ai & Bj > x.
Пусть B — максимальное количество бит в числах во вводе. Тогда |f(x, S)| может быть вычислено за время O(|S| + 3B) для всех x (используя метод перебора всех подмножеств битов x). Величины g(x) могут быть вычислены за время O(3B), однако в этом случае нужно использовать перебор не всех подмножеств битов x, а всех надмножеств.
Общее время работы описанного решения O(P + M + K + 3B) (B = 16).
Задача C. Пчёлы
Автор задачи — jakubr (Jakub Radoszewski)
Имя входного файла: stdin
Имя выходного файла: stdout
Ограничение по времени: 5 секунд
Ограничение по памяти: 512 мегабайт
Хобби пчеловода Байтазара — изучение фигур, которые образованы в сотах приносимым пчёлами мёдом. Каждая такая фигура представляет собой связное множество шестиугольных ячеек со стороной 1, внутри которого нет «дырок».
Более формально, назовём фигурой без «дырок» подмножество единичных шестиугольников правильной шестиугольной сетки такое, что любые два единичных шестиугольника, ему принадлежащие, соединены путём, все шестиугольники которого также принадлежат этому множеству и любые два соседних (в смысле этого пути) шестиугольника имеют общую сторону, а любые два единичных шестиугольника, не принадлежащие этому подмножеству, соединены путём, ни одна из клеток которого не принадлежит этому множеству и любые два соседних (в смысле этого пути) шестиугольника имеют общую сторону.
Байтазар хочет составить полный список возможных значений периметра и количества ячеек в подобных шаблонах. Он попросил Вас написать программу, которая по двум заданным числам n и p выясняет, существует ли фигура без «дырок», состоящая из n ячеек, периметр которой равен p.
Например, на приведённой ниже картинке n = 4, а p = 18.

Формат входного файла. Первая строка ввода содержит количество тестовых примеров T (1 ≤ T ≤ 1000). Каждая из последующих T строк задаёт тестовый пример и содержит два целых числа n и p (1 ≤ n, p ≤ 1000) — требуемые площадь и периметр фигуры.
Формат выходного файла. Для каждого тестового примера в порядке их следования во входном файле выведите ответ в отдельной строке. В случае, если фигур с заданными параметрами не существует, выведите «NO». В противном случае выведите строку из p символов, составленную из букв «L» и «R», задающую обход вдоль периметра фигуры (по часовой стрелке или против неё), при этом «L» обозначает левый поворот, а «R» — правый.
Если корректных ответов несколько, выведите любой из них.
| stdin | stdout |
| 3 4 18 3 18 3 12 |
RLRRRRLRLRLRRRRLRL NO LRRRLRRRLRRR |
Решение задачи C
Задача заключается в том, чтобы построить многоугольник на шестиугольной решётке,
состоящий из n единичных клеток и p сторон, или же убедиться, что многоугольника с данными параметрами не существует.
Зафиксируем количество клеток n и изучим возможные значение p такие, что многоугольник с p сторонами существует. Очевидно, что p должно быть чётным.
Также легко заметить, что p не может быть больше, чем 4n + 2 (периметр многоугольника, состоящего из n клеток, идущих подряд и граничащих по стороне; назовём такой многоугольник цепочкой).
С другой стороны, из общих соображений ясно, что многоугольник минимального периметра представляет собой некое подобие большого шестиугольника. Формально его периметр задаётся формулой  .
.
Оказывается, что данные ограничения являются не только необходимыми, но и достаточными.
Алгоритм построения выглядит следующим образом: мы начинаем с цепочки, состоящей из n клеток и имеющего максимальный периметр. Далее, пока периметр нашего многоугольника больше, чем p, мы удаляем одну клетку из «хвоста» многоугольника и добавляем эту клетку в «голову», достраивая большой шестиугольник слой за слоем (см. стрелку 1 на иллюстрации).

Данный ход уменьшает периметр на 2, 4 или 6, так что в конечном итоге нам придётся увеличивать периметр на 2 или 4, перемещая некоторые клетки (например, перемещение клетки из «хвоста» в соответствии со стрелкой 2 на рисунке).
При некоторых реализациях потребуется отдельно разобрать случаи для малых значений n, а также случаи, когда периметр близок к минимальному значению для данного n.
Задача D. Анюта и кубики
Автор задачи и разбора — Tomasz Idziasek.
Имя входного файла: stdin
Имя выходного файла: stdout
Ограничение по времени: 2 секунд
Ограничение по памяти: 512 мегабайт
Маленькая Анюта любит играть с кубиками. У неё есть N позиций, расположенных в ряд и пронумерованных от 1 до N, в которых она любит строить башни из кубиков.
Башня — это несколько кубиков, лежащих один на другом. Высота башни — это количество кубиков в ней. Номер башни соответствует номеру позиции, в которой эта башня строится.
Изначально все позиции пусты. Каждую минуту происходит следующее.
- Анюта смотрит последовательно на позиции с номерами от N — 1 до 1.
- Если в какой-то позиции i есть кубики, и высота башни больше либо равна высоте башни в позиции i + 1, Анюта перекладывает один кубик из i-й позиции в (i + 1)-ю.
- После того, как Анюта просмотрела все позиции, она добавляет один кубик в башню в позиции с номером 1.
Пример. Пусть количество позиций N = 6, а высоты башен равны 5 0 1 3 4 1 (нумерация позиций от 1 до N слева направо). Тогда за следующую минуту произойдет следующее.
- Анюта посмотрит на позицию 5: высота башни в ней равна 4, в то время как высота башни в следующей позиции равна 1. Анюта перенесёт один кубик из позиции 5 в позицию 6. Высоты башен станут равными 5 0 1 3 3 2.
- Анюта посмотрит на позицию 4: высота башни в ней равна 3, а высота башни в следующей позиции равна 3. Анюта перенесёт один кубик из позиции 4 в позицию 5. Высоты башен станут равными 5 0 1 2 4 2.
- Из позиции 3 в позицию 4 Анюта не будет переносить кубик, потому что высота башни в позиции 4 больше, чем высота башни в позиции 3.
- Из позиции 2 в позицию 3 Анюта не будет переность кубик, потому что в позиции 2 нет кубиков.
- Наконец, из позиции 1 в позицию 2 Анюта перенесёт один кубик. Высоты башен станут равными 4 1 1 2 4 2.
- После этих действий Анюта добавит один кубик в позицию номер 1, и высоты башен станут равными 5 1 1 2 4 2.

Изменение высот башен в течение минуты в описанном выше примере
Однажды Анюте надоело играть, и она решила посчитать, сколько у неё будет кубиков на определённых позициях после некоторого числа минут. Поскольку Анюта ещё маленькая, а кубиков так много, она обратилась за помощью к вам.
Более формально, вам требуется ответить на Q запросов вида «сколько будет в сумме кубиков в башнях с номерами от Si до Fi включительно после Bi минут». Запросы независимы: в каждом запросе считается, что изначально все позиции пусты, а после этого проходит i>Bi минут.
Формат входного файла. В первой строке ввода находятся два целых числа Nи Q (2 ≤ N ≤ 1018, 1 ≤ Q ≤ 100 000) — количество позиций для башен и количество запросов соответственно. В каждой из следующих Qстрок находится три целых числа Si, Fi и Bi (1 ≤ Si ≤ Fi ≤ N, 1 ≤ Bi ≤ 1018) — начальная и конечная позиции для запроса и количество минут, прошедшее после начала Анютиных действий.
Формат выходного файла. Выведите Q строк, по одной на каждый запрос. В каждой строке выведите одно число — ответ на запрос. Отвечайте на запросы в порядке их следования во вводе.
Примеры
| stdin | stdout |
| 10 3 1 1 1 1 10 100 10 10 11 |
1 100 2 |
| 1000000000000 2 1 1234 412412314 100000000000 999999999999 1000000000010 |
1234 900000000006 |
Решение задачи D
Для начала следует понять, как движутся кубики по позициям. Рассмотрим, к примеру, случай, когда N = 5.
В первые пять минут кубики будут <<ползти>> один за одним от позиции номер 1 до позиции N, пока в каждой позиции не появится по одному кубику и высоты башен будут равны [1, 1, 1, 1, 1].
На шестой минуте кубик из четвёртой позиции перейдёт в пятую, кубики левее подвинутся на одну позицию вправо, и в позиции номер 1 появится новый кубик: [1, 1, 1, 1, 2].
На седьмой минуте произойдёт перемещение кубиков только из позиций (3,2,1) в позиции (4,3,2) соответственно, и высоты станут [1, 1, 1, 2, 2].
На восьмой минуте передвинутся кубики из позиций 1-4: [1, 1, 1, 2, 3].
Продолжая моделирование, получим:
- 9-я минута: [1, 1, 2, 2, 3]
- 10-я минута: [1, 1, 2, 3, 3]
- 11-я минута: [1, 1, 2, 3, 4]
Спустя ещё 4 минуты высоты башен станут равны [1, 2, 3, 4, 5]. Спустя ещё 5 минут высоты станут [2, 3, 4, 5, 6], спустя ещё 5~ — [3, 4, 5, 6, 7].
Таким образом, нетрудно заметить следующую закономерность:
- В первые N минут высоты башен равны [1, ..., 1, 0, ..., 0];
- Далее высоты башен имеют вид либо [1, ..., 1, 2, 3, ..., x], либо [1, ..., 1, 2, 3, ..., k — 1, k, k, k + 1, ..., x];
- Спустя
 минут после начала высоты башен имеют вид [1, 2, 3, ..., N — 1, N];
минут после начала высоты башен имеют вид [1, 2, 3, ..., N — 1, N]; - После этого по одному кубику добавляется во все башни по кругу.
Учитывая вышесказанное, для ответа на каждый запрос нужно сначала вычислить, какой вид сейчас имеют высоты башен, а затем применить несколько несложных математических формул, связанных с арифметическими прогрессиями.
Задача E. Математическая магия
Автор задачи и рабора — Олег Христенко
Имя входного файла: stdin
Имя выходного файла: stdout
Ограничение по времени: 2 секунд
Ограничение по памяти: 512 мегабайт
Как-то раз Вася готовился к олимпиаде по математике и заснул. Васе приснился Дэвид Блейн, говорящий следующее:
«Сейчас я продемонстрирую математическую магию. Вот смотрите: я выписываю на доске в ряд N целых положительных чисел, больших единицы и меньших 263. Некоторые из этих чисел повторяются: хотя бы одно из них равно какому-то другому числу в ряду. Под ними я выписываю на доске ряд из K < N целых положительных чисел, больших единицы и меньших 263, некоторые из них тоже повторяются. Перемножаем числа в обоих наборах… произведение чисел из второго набора ровно на единицу больше, чем произведение чисел из первого набора.
А сейчас я убираю некоторые повторения в верхнем ряду чисел: множество чисел, присутствующих в верхнем ряду, осталось таким же, но хотя бы один элемент ряда я стираю. Делаю то же самое с нижним рядом… вновь ни одно число ряда не пропало совсем, просто некоторых чисел стало меньше. Снова перемножаем наборы… и видим, что произведение чисел из второго набора снова ровно на единицу больше, чем произведение чисел из первого набора. Магия!»
Вася проснулся, но смог вспомнить только N. Помогите ему восстановить фокус.
Формат входного файла. В первой строке входного файла задано одно целое число N (2 ≤ N ≤ 100) — количество чисел в первоначально выписанном Дэвидом Блейном наборе.
Формат выходного файла. В первой строке выведите первоначально выписанный Дэвидом Блейном набор, во второй — тот, который был написан снизу, в третьей и четвёртой — варианты этих наборов после произведённых Дэвидом вычёркиваний. Числа внутри каждого набора должны быть отсортированы по неубыванию, должны быть больше единицы и не должны превышать 263 — 1.
Если наборов, удовлетворяющих условию и ограничениям, не существует, выведите вместо них одно слово «Impossible». Если таких наборов несколько, выведите любой из них.
| stdin | stdout |
| 2 | Impossible |
| 3 | 2 2 2 3 3 2 3 |
Разбор задачи E
Для N = 2 решения не существует (так как K<N, то в нижней части выписано одно число, и вычеркнуть кратные не получается). Для N = 3 решение — 8, 9, 2, 3 ({222}, {33}, {2}, {3}).Можно показать, что данное решение единственно. Для N = 4 решения не существует. Доказательство приводится в конце разбора.
Построим решение для N ≥ 5.
Для любого N > 4 берём числа 2(2N-3-1)и 2N-1(2N-3-1) в качестве b и a.
Очевидно, что они представимы как произведение некоторого количества двоек и числа 2N-3-1, a представлено в виде произведения N сомножителей, и a делится на b. Проверим условия на a+1 и b+1. a + 1 = (2N-2 — 2) + 1 = 2N — 2 — 1, а b + 1 = 2N-2 (2N-2 — 2) + 1 = (2N-2)2 — 2 * 2N-2 + 1= (2N-2 — 1)2, то есть получаем, что a + 1 = (b +1)2, и тем самым
получаем наборы из двух и одного числа соответственно, удовлетворяющие условию задачи.
Для 5 ≤ N ≤ 65 сгенерированный таким образом ответ подходит автоматически.
Далее заметим, что если набор q1,..., qk является решением задачи для N = k, и qk = r1 · r2, то набор q1,..., qk-1, r1,r2 является решением задачи для N=k+1 (просто представляем в разложении числа b число {qk} как произведение чисел r1 и r2). Аналогично разложение одного из множителей на произведение двух меньших переводит пару (a+1), (b+1) также в корректную пару.
Поэтому будем пытаться раскладывать 2N-3 — 1 на множители, не превосходящие 263 — 1, тем самым получая из той же формулы решения для чисел от N + 1 до N +D — 1, где D — число простых делителей числа 2N-3 — 1. В случае N > 65 требуется ещё разложить 2N-2 — 1 на множители, не превосходящие 263 — 1.
Еcли N имеет остаток 0 по модулю 6, то N — 2 делится на 2, N — 3 делится на 3, и тем самым 2N-2 — 1 представляется как (2(N-2)/2 — 1)(2(N-2)/2 + 1), а 2N-3 — 1 — как (2(N-3)/3 — 1)(2(2N-6)/3 + 2(N-3)/3 + 1). Легко увидеть, что при N ≤ 95 оба сомножителя не превосходят 263 — 1. А раз так, то и все последующие их разложения также удовлетворяют требованиям задачи.
Если N имеет остаток 5 по модулю 6, то N — 2 делится на 3, а N — 3 — на 2, соответственно, используем аналогичное разложение.
Таким образом, начинаем с N = 63 (260 -1 должно раскладываться на большое количество множителей, а 261-1 требованию задачи удовлетворяет), а затем перебираем все N, не превосходящие 96 и дающие 0 или 5 при делении на 6, делая первое разложение 2N-3 — 1 на множители описанным в предыдущем абзаце способом (после чего раскладывая каждый из множителей <<до упора>>) и, также в соответствии с этим способом, раскладывая 2N-2 — 1 на два множителя. При этом, количество множителей K в наборе a + 1 будет равно четырём (квадрат числа переходит в квадрат произведения двух чисел), тем самым условие K < N выполняется.В результате перебора получаем, что:
- При N = 63 получаем D = 13 множителей, то есть генерируем ответы для 64 ≤ N ≤ 75.
- При N = 71 получаем D = 7 множителей, генерируем ответы для N от 72 до 77 включительно.
- При N = 77 получаем D = 4 множителя, генерируем ответы для N от 78 до 81 включительно.
- При N = 78 получаем D = 7 множителей, генерируем ответы для N от 79 до 84 включительно.
- При N = 83 получаем D = 11 множителей, генерируем ответы для N от 84 до 93 включительно.
- При N = 90 получаем D = 6 множителей, генерируем ответы для N от 91 до 95 включительно.
- При N = 95 получаем D = 9 множителей, генерируем ответы для N от 96 до 100 (даже до 104) включительно.
Тем самым алгоритм находит решения для всех N ≤ 100.
Доказательство невозможности решения при N = 4
Так как N = 4, то, по условию задачи, a + 1 раскладывается на три множителя или менее. Чтобы было, что вычёркивать, как минимум два из них должны повторяться. Также, по условию задачи, a делится на b, то есть a = xb, x > 1.
Cначала разберём все варианты набора для a + 1 (и соответствующего набора для b + 1):
- u2, ~u;
- u3, ~u;
- uv2, uv;
- u3, u2.
В случае 3 a + 1 = uv2. Тогда b + 1 = uv; xb + 1 = uv2, вычитаем, uv(v — 1) = b(x — 1). Так как uv и b взаимно просты, то v — 1 делится на b, так как v > 1, то v — 1 = yb ≥ bnobr>, v ≥ b + 1. Так как u > 1, то uv > v ≥ b + . Противоречие.
Так как в данном рассуждении не использовалось то, что u ≠ v, то случай a + 1= u3 и b + 1 = u2 рассмотрен автоматически.
Остались случаи 1 (u2,~u) и 2 (u3,~u). Для них рассмотрим варианты набора из четырёх множителей для a и cоответствующего им набора для b.
I. a = x2yz, b = xyz;
II. a = x2y2, b = xy2;
III. a = x3y, b = x2y;
IV. a = x4, b = x3;
V. а = x2y2, b = xy;
VI. a = x4, b = x2;
VII. a = x3y, b = xy;
VIII. a = x4, b = x.
Варианты II-IV получаются из варианта I путём подстановки z = y, z = x и z = y = x соответственно. Аналогично, вариант VI есть частный случай варианта V.
В варианте I заменим yz на t.
1. x2t + 1 = v2, xt + 1 = v, откуда x2t + 1 = x2t2 + 2xt + 1. Так как все слагаемые положительны и x2t2 > x2t (так как t > 1), то правая часть больше левой.
2. x2t + 1 = v3, xt + 1 = v. Аналогичной подстановкой и раскрытием скобок получаем x2t = x^3t3 + 3x2t2 + 3xt, все слагаемые положительные, x2t < x3t3.
Вариант V
1. x2y2 + 1 = v2. Сразу не бывает при целых x, y, v > 1.
2. x2y2 + 1= v3, xy + 1 = v. При подстановке и приведении подобных получим, что сумма (xy)3 + 2(xy)2 + 3xy равна 0, что невозможно при x,y > 1.
Вариант VII
1. x3y + 1 = v2, xy + 1 = v, перепишем как x3y + 1 = x2y2 + 2xy + 1 и затем как xy(x2 — xy) = 2. Получается, что 2 делится на xy, чего при x > 1 и y > 1 не может быть.
2. x3y + 1 = v3, xy + 1 = v. Подставляем, получаем, что x3y = x3y3+ ... (многоточием обозначены заведомо положительные числа), что при y > 1 невозможно.
Вариант VIII
Пусть x4 + 1 делится на x + 1. Но x4 + 1 = (x + 1)(x — 1)(x2 + 1) + 2, то есть получаем, что 2 делится на x + 1. Противоречие с тем, что x > 1.
Мы разобрали все случаи и везде пришли к противоречию, то есть при N = 4 решения не существует.

Задача F. Зебра Гиппо и полоски
Автор задачи и рабора — rng58 (Makoto Soejima)
Имя входного файла: stdin
Имя выходного файла: stdout
Ограничение по времени: 2 секунд
Ограничение по памяти: 512 мегабайт
У зебры Гиппо есть 1018 полосок, занумерованных последовательными целыми числами от 0 до 1018 — 1. В момент времени 0 только полоска с номером 5⋅ 1017 является чёрной, остальные являются белыми. В момент времени t (t > 0) цвет полосок удовлетворяет следующим правилам:
- Если x-я полоска в момент времени t — 1 является чёрной, то она будет чёрной и в момент времени t.
- Если в момент времени t — 1 все полоски, расположенные на расстоянии не более, чем D от x-й полоски, являются белыми (иначе говоря, для каждого целого неотрицательного y, меньшего 1018 и удовлетворяющего неравенству |x — y| ≤ D, y-я полоска в момент времени t-1 является белой), то в момент времени t x-я полоска также будет
белой. - В ином случае цвет x-й полоски в момент времени t выбирается произвольным образом.
Вычислите количество возможных различных раскрасок зебры по модулю 109 + 7 в момент времени t. Две раскраски зебры считаются различными, если цвет хотя бы одной полоски различается.
Формат входного файла. В первой и единственной строке входа заданы два целых числа t и D (1 ≤ t ≤ 109, 1 ≤ D ≤ 50), разделённые пробелом.
Формат выходного файла. Выведите одно целое число — остаток от деления количества возможных раскрасок в момент времени t на 109 + 7
Пример
| stdin | stdout |
| 5 1 | 2 3 |
| 2 3 | 1849 |
Разбор задачи E
Из соображений симметрии очевидно, что количество раскрасок зебры является квадратом количества раскрасок её правой половины. Так что далее будем рассматривать только правую половину зебры. Для упрощения перенумеруем полоски следующим образом: 500 000 000 000 000 000+x-ю занумеруем как x-ю.
Для начала решим более простую задачу: дана раскраска, требуется вычислить минимальное время t, по истечении которого данная раскраска будет достижима. Эта задача решается следующим алгоритмом:
Изначально указатель находится на полоске с номером 0, а множество A пусто.
Цикл:
- Если указатель находится на самой правой полоске, выходим из цикла.
- Пусть x — текущая позиция указателя.
- Найдём наибольшее d (0 < d ≤ D) такое, что (x+d)-я полоска чёрная. Если такого d нет, алгоритм завершается неудачно.
- Добавляем d в множество A и передвигаем указатель на (x+d)-ю полоску.
Конец цикла.
Если этот алгоритм успешно завершается, минимальное время t равно количеству элементов множества A.
Пусть f (a1,a2,..., ak) — количество раскрасок, для которых вышеприведённый алгоритм возвращает
A ={a1, a2,..., ak}.
Алгоритм возвращает {a1, a2,..., ak} для данной раскраски тогда и только тогда, когда:
- 0-я, a1-я, (a1+a2)-я и так далее полоски — чёрные.
- Для каждого i полоски между (a1+...+ai+1)-й и (a1+...+ai-1+D)-й являются белыми.
Отсюда получаем f(a1, a2,..., ak) = 2a1-1 + a1+a2-D-1 + a2+a3-D-1 +....
В первоначальной задаче нам нужно посчитать количество раскрасок, то есть сумму f(a1, a2,..., ak) (при k ≤ T).
Пусть dp[t][a] (t ≤ T, a ≤ D) — сумма f (a1, a2,..., at-1, a).
Получаем следующее рекуррентное соотношение для динамического программирования:
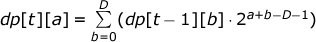
Ответом к задаче является 1 + dp[1][D] +… + dp[T][D], тем самым сложность задачи равна O(TD).
Чтобы ускорить решение, можно использовать возведение матрицы в степень. Пусть vt — вектор (dp[t][0],…, dp[t][D]). Из рекуррентного соотношения мы знаем, что vt+1 = vt · A для всех t (A — некоторая матрица размерности
(D+1) × (D+1)).
Ответ к задаче будет равен последнему элементу v0 ⋅ (A + A2 +… + AT), увеличенному на единицу.
Сложность этого алгоритма — O(D3 ⋅ log T).

Конкуренция на чемпионате была очень высокой. В финале участвовали коллеги Геннадия Короткевича по команде НИУ ИТМО чемпионы ACM ICPC 2013 Нияз Нигматуллин (Niyaz Nigmatullin) и Михаил Кевер (mikhailOK), победитель Facebook Hacker Cup, Google Code Jam и Яндекс.Алгоритма 2011, один из самых титулованных спортивных программистов мира Пётр Митричев (Petr), вице-чемпион VK Cup 2012 Ван Циньши (s-quark) из Китая и другие сильные спортивные программисты.
В финал вышли представители России, Беларуси, Украины, Польши, Словакии, Тайваня, Китая и Южной Кореи. Среди них — разработчики из Google, «Вконтакте» и Facebook.
Автор: EgorK







