Последние десятилетия мировая экономика регулярно попадает в водоворот финансовых кризисов. 1987, 1997, 2008 чуть не привели к коллапсу существующей финансовой системы, именно поэтому ведущие специалисты начали разрабатывать методы, с помощью можно контролировать неопределенность, господствующую в финансовом мире. В Нобелевских премиях последних лет (полученных за модель Блэка-Шоулза, VaR, и т.д.) отчетливо прослеживается тенденция к математическому моделированию экономических процессов, попыткам предсказать поведение рынка и оценить его устойчивость.
Сегодня я постараюсь рассказать о наиболее широко применяемой методике предсказаний потерь — Value at Risk (VaR).
Понятие VaR
Понятное экономисту объяснение VaR звучит следующим образом: «Выраженная в денежных единицах оценка величины, которую не превысят ожидаемые в течение данного периода времени потери с заданной вероятностью». По-сути, VaR — это величина потерь по инвестиционному портфелю за фиксированный промежуток времени, в случае, если случится некоторое не благоприятное события. Под «не благоприятными событиями» можно понимать различные кризисы, слабо предсказуемые факторы (изменения в законодательстве, природные катаклизмы, ...), которые могут повлиять на рынок. В качестве временного горизонта, обычно выбирают один, пять или десять дней, в силу того, что на больший срок предсказать поведение рынка крайне сложно. Уровень допустимого риска (по-сути доверительный интервал) берется равным 95% или 99%. Также, конечно, фиксируется валюта, в которой мы будем измерять потери.
При вычислении величины предполагается что рынок будет вести себя «нормальным» образом. Графически это значение можно проиллюстрировать так:
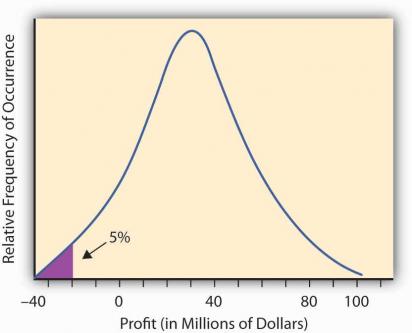
Методы расчета VaR
Рассмотрим наиболее часто применяемые методы вычисления VaR, а так же их преимущества и недостатки.
Историческое моделирование
При историческом моделировании мы берем уже известные из прошлых измерений значения финансовых колебаний для портфеля. К примеру, у нас есть поведение портфеля на протяжении предыдущих 200 дней, на основе которых мы решаем вычислить VaR. Предположим, что на следующий день финансовый портфель будет вести себя также, как в один из предыдущих дней. Таким образом, мы получим 200 исходов на следующий день. Далее, мы допускаем, что случайная величина распределена по нормальному закону, основываясь на этом факте, мы понимаем, что VaR — это один из перцентилей нормального распределения. В зависимости от того, какой уровень допустимого риска мы взяли, выбираем соответствующий перцентиль и, как следствие, получаем интересующие нас значение.
Недостатком этого метода является невозможность построения предсказаний по портфелям, о которых у нас нет сведений. Также может возникнуть проблема, в случае, если составляющие портфеля существенно изменятся за короткий промежуток времени.
Хороший пример вычислений можно найти по следующей ссылке.
Метод ведущих компонент
Для каждого финансового портфеля можно вычислить набор характеристик, помогающих оценить потенциал активов. Эти характеристики называются ведущими компонентами и, обычно, представляют собой набор частных производных от цены портфеля. Для вычисления стоимости портфеля обычно используется модель Блэка — Шоулза, о которой я постараюсь рассказать в следующий раз. В двух словах, модель представляет собой зависимость оценки европейского опциона от времени и от его текущей стоимости. Основываясь на поведении модели мы можем оценить потенциал опциона, анализируя функцию классическими методами математического анализа (выпуклость/вогнутость, промежутки возрастания/убывания и т.д.). Базируясь на данных анализа, VaR рассчитываются для каждой из компонент и результирующее значение строиться, как комбинация (обычно взвешенная сумма) каждой из оценок.
Метод Монте-Карло
Метод Монте-Карло во многом похож на метод исторического моделирования, разница в том, что вычисление производится не на основе реальных данных, а на случайно сгенерированных значениях. Преимуществом такого метода является возможность рассмотрения, как большого числа ситуаций, так и эмулирование поведения рынка в экстремальных условиях. Явным недостатком являются большие вычислительные ресурсы, требуемые для реализации такого подхода. При работе с этой методикой обычно используются NoSQL хранилища и распределенные вычисления на базе MapReduce. Хороший пример использования Hadoop для вычисления VaR можно найти по следующей ссылке.
Естественно, это не единственные методики вычисления VaR. Существуют как простые линейные и квадратичные модели предсказания цены, так и достаточно сложный метод вариаций-ковариаций, о которых я не рассказал, но интересующиеся смогут найти описание методик в нижеприведенных книгах.
Критика методики
Важно отметить, что при подсчете VaR принимается гипотеза о нормальном поведении рынка, однако, если бы это допущение было верным, крисизы случались бы раз в семь тысяч лет, но, как мы видим, это абсолютно не верно. Нассим Талеб, известный трейдер и математик, в книгах «Одураченные случайностью» и «Черный лебедь» подвергает существующую систему оценки рисков жесткой критике, а также предлагает свое решение, в виде использования другой системы расчета рисков, базирующейся на логонормальном распределении.
Несмотря на критику, VaR вполне успешно используется во всех крупнейших финансовых институтах. Стоит отметить, что данный подход не всегда применим, в силу чего, были созданы другие методики со схожей идеей, но другим методом расчета (например, SVA).
С учетом критики были разработаны модификации VaR, основанные либо на других распределениях, либо на других методиках расчетов на пике Гауссовой кривой. Но об этом я постараюсь рассказать уже в другой раз.
Ссылки
Несколько интересных книг по теме:
- Опционы, фьючерсы и другие производные финансовые инструменты
- Черный лебедь. Под знаком непредсказуемости
- Одураченные случайностью. О скрытой роли шанса в бизнесе и в жизни
Автор: Silf