В минувшую субботу прошел второй квалификационный раунд олимпиады по программированию Russian Code Cup 2012.

Russian Code Cup — индивидуальное соревнование по спортивному программированию, ежегодно проводимое Mail.Ru Group. Оно традиционно состоит из трех этапов: в начале лета проходят три квалификационных раунда, затем лучшие принимают участие в отборочном туре, первые пятьдесят победителей отборочного тура соревнуются в финале. Личного присутствия потребует только последний из них, остальные же проводятся онлайн. Все финалисты будут отмечены ценными подарками, а приз участнику, занявшему первое место, составит 10 000 долларов. За второе и третье место полагаются 5 000 и 3 000 долларов.
В данной статье я подробно разберу задачи, вынесенные на конкурс, а также поделюсь статистикой раунда. Я постарался разъяснить детали настолько, чтобы решение задач было понятно даже тем, кто еще делает первые шаги. Также данный материал поможет получить представление, какой сложности задачи предлагаются на отборочных этапах чемпионата по программированию Russian Code Cup.
В это воскресенье, 10 июня, в 11:00, будет проходить последний квалификационный раунд, из которого две сотни участников перейдут в «полуфинал» — отборочный раунд. На втором раунде для этого достаточно было решить две задачи — одну простую и одну сложную, и уложиться при этом в половину отведенного времени. Ждем вас в воскресенье и желаем удачи!
Ну а теперь перейдем к задачам.
«Простая задача»
Очевидно, что эта задача с «говорящими» названием и содержанием была для разогрева — ее нужно было решить быстро и с первой попытки. Программе участника следовало дать ответ, является ли задача простой, проверив критерии простой задачи. На входе давалось количество операторов ветвления (ОВ) и операторов цикла (ОЦ) и следовало вывести «yes» в одном из двух случаев:
— не более 1 ОВ и не более 2 ОЦ,
— не более 2 ОВ и не более 1 ОЦ.
Во всех прочих случаях следовало выводить «no».
Разбирать эту задачу здесь детально, наверное, не имеет смысла — она и правда очень простая.
Тут интересно то, что решение данной задачи рекурсивно подходит под определение простой задачи. Одним из наиболее элегантных ее решений является проверка суммы квадратов введенных значений: (ОВ*ОВ + ОЦ*ОЦ) < 6.
Всего было направлено на проверку 1261 решение, из них правильных 722 (57%). 77% участников Russian Code Cup справились с этой задачей. Первое решение пришло от Андрея Максая через 1 минуту 37 секунд после начала раунда.
«Ключ»
Эта задача немного сложнее. По условию задачи наша строка зеркально отображается относительно центра зашифрованной строки, следовательно, шифр представляет собой следующую конструкцию:
(N символов)строка(M символов)акортс(N символов),
для всех случаев, когда префикс и суффикс не пересекаются друг с другом. Пример, когда такое возможно, демонстрировался в условии задачи — тогда суффикс и префикс определяли одни и те же символы: ababc являлось зашифрованной bab.
Очевидно, что для восстановления строки необходимо найти последовательность, имеющую точное зеркальное отражение. То есть максимальная непрерывная последовательность позиций i, для которых выполняется условие s[i] = s[l — i — 1], составляет искомую строку.
Для этого можно посчитать для каждой позиции i значение k — длину наибольшей подстроки s[i—k..i], в которой все символы удовлетворяют нашему условию. Найденные значения сохраняем в массиве, после чего в нем находим позицию самого левого вхождения максимального значения.
Для расчета длины подстроки p[i] будем использовать уже рассчитанное значение p[i—1], это сильно сократит время и ресурсы.
- p[i] = 0, если s[i] <> s[l — i — 1]
- p[i] = 1, если i=0 и s[0] = s[ l —1]
- p[i] = p[i-1] + 1, если i>0 и s[0] = s[l — i — 1]
| № | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симв | c | x | b | a | y | d | z | a | b | x | e |
| s[i]=s[l-i-1]? | c=e? | x=x? | b=b? | a=a? | y=z? | d=d? | z=y? | a=a? | b=b? | x=x? | e=c? |
| ответ | нет | да | да | да | нет | да | нет | да | да | да | нет |
| p[i] | 0 | 0+1= | 1+1= | 2+1= | 0 | 0+1= | 0 | 0+1= | 1+1= | 2+1= | 0 |
| 0 | 1 | 2 | 3 | 0 | 1 | 0 | 1 | 2 | 3 | 0 | |
| max | 3 | 3 | 0 |
Ответом будет подстрока длины p[max], заканчивающаяся в символе с номером max, где max — позиция самого левого вхождения максимального значения в массиве p.
Всего на проверку было направлено 1158 решений, из них правильных 337 (29%). 36% участников Russian Code Cup QR2 справились с этой задачей. Первое решение пришло от Куртова Николая через 9 минут после начала раунда.
«Тетраэдр»
На первой квалификации задача со спичками была самой простой: нужно было посчитать, можно ли из указанного набора сложить параллелепипед. Сложить тетраэдр из тех же спичек оказалось не настолько просто — первое правильное решение пришло через 30 минут после начала турнира.
Напомню, что тетраэдр — это многогранник, гранями которого являются четыре треугольника (другими словами — треугольная пирамида).
Все начинается с того, что мы перебираем возможные соответствия спичек ребрам тетраэдра. Обозначим искомый тетраэдр как ABCD. У него шесть ребер: AB, AC, AD, BC, BD и CD. Переберем все 6! = 720 вариантов, какая спичка соответствует какому ребру. Теперь осталось проверить, что соответствующий тетраэдр существует.
Как проверить существование тетраэдра? Здесь есть как минимум три решения.
Первое решение основывается на вычислении объема тетраэдра. Самое простое решение —найти формулу для расчета объема тетраэдра по граням. Эта задача сама по себе непростая, приведу здесь формулу:
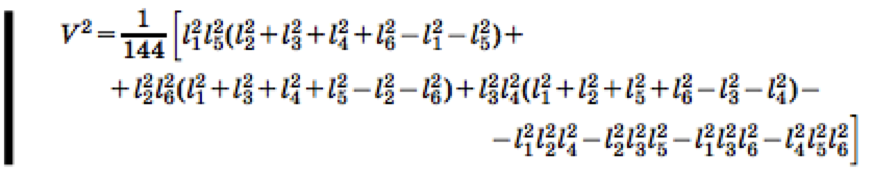
Соответственно, если правая часть равенства оказывается отрицательной, тетраэдр не сойдется.
Для интересующихся — здесь эта формула выводится: http://www.mccme.ru/free-books/mmmf-lectures/book.21.pdf
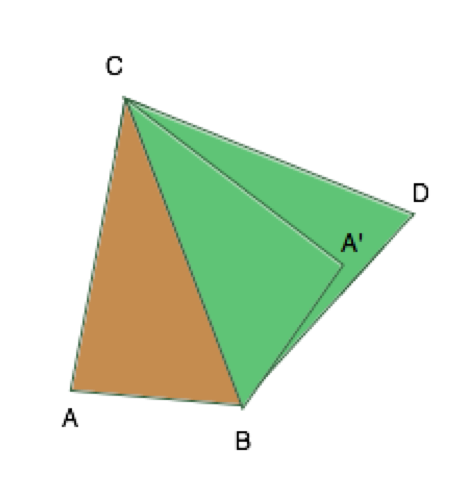
Второй подход к решению задачи — геометрический. Сначала убедимся, что ABC и BCD существуют. Теперь попытаемся сделать тетраэдр. Понятно, что при построении объемной фигуры проблема может возникнуть только с последним ребром — оно может оказаться или слишком длинным, или слишком коротким. Поэтому в этом решении предлагается найти диапазон длины последнего ребра.
Есть два предельных варианта размещения граней, при которых тетраэдр превращается в плоскую фигуру. Первый — когда грани развернуты друг относительно друга на 180 градусов (CAB и CBD), и вторая — когда они «сложены» и образуют «нулевой угол» (CA’D и CDB). Все допустимые положения граней друг относительно друга находятся в диапазоне между этими граничными. Наибольшей своей длины последнее ребро (A-D) достигает в первом предельном варианте (AD), а наименьшей — в последнем (A’D). Следовательно, тетраэдр будет существовать, если эта длина последнего ребра укладывается в найденный нами диапазон (от A’D до AD).
Для того чтобы найти расстояние между точками A и D и A’ и D, найдем сначала их координаты, приняв за ноль одну из общих для треугольников вершин, а ось абсцисс проведем через одно из ребер, исходящих из этой вершины. Найти координаты всех остальных вершин в этой системе координат довольно просто: через соотношения сторон и косинусы углов мы определим положения вершин в полярных координатах (угол, расстояние), после чего переведем их в декартову систему координат. Зная координаты вершин, вычислить максимальное и минимальное расстояния между несвязанными вершинами совсем просто.
Программа должна проверять, умещается ли длина оставшейся грани в указанные диапазоны. Если да, то тетраэдр из таких длин «собрать» можно.
Третий способ также геометрический. Сначала необходимо проверить существование всех треугольников с указанными сторонами. Если хотя бы один треугольник не может быть построен по указанным значениям сторон, то тетраэдр также не может быть построен. Для проверки необходимо проверить неравенство невырожденного треугольника — любая из его сторон должна быть строго меньше суммы двух других.
Во многих случаях решение этим и ограничилось; между тем существуют ситуации, когда треугольники с указанными сторонами могут быть построены, а тетраэдр из них собрать невозможно.
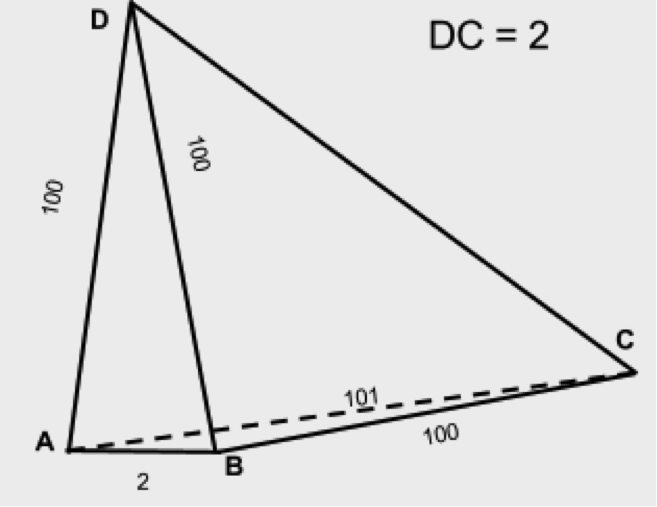
Например, если мы имеем грани (100,100,2,101,100,2), то треугольники (100,100,2) и (101,100,2) формально удовлетворяют неравенству треугольника, но тетраэдр сложить из таких треугольников невозможно. Из рисунка мы видим, что ребро AC почти параллельно AB, значит, расстояние от D до C почти не будет меняться при любом наклоне грани ABD относительно AB, из чего можно заключить, что DB почти перпендикулярно BC. В этом случае DC можно приблизительно оценить как корень из суммы квадратов катетов, то есть DC должно быть приблизительно около 10, а совсем не 2, как мы предположили в условии.
Следовательно, кроме проверки на треугольники в гранях, необходимо выполнить дополнительную проверку на трехгранные углы. Необходимых и достаточных условий существования трехгранного угла два:
- сумма плоских углов трехгранного угла должна быть меньше 360 градусов,
- каждый плоский угол трехгранного угла должен быть меньше суммы двух других плоских углов.
Плоский угол находится через теорему косинусов для треугольника.
Всего было направлено на проверку 1088 решений, из них правильных всего 74 (7%). 8% участников Russian Code Cup QR2 справились с этой задачей. Первое решение пришло от участника с ником AVictor через 30 минут после начала раунда.
«Задачи»
По условию задачи было необходимо найти подмножество конкурсных задач, для которых выполнялись бы требования: 1) одна задача каждого уровня сложности, 2) каждая тема представлена, 3) никакие две задачи не пересекаются по темам. Входные данные содержали описания задач: какой набор тем каким задачам соответствует и какова сложность задач. На выходе нужно было отобразить требуемое подмножество задач в виде их индексов (номеров) или вывести Impossible, если такого подмножества не существует.
Ключевым решением в данной задаче является выбор метода динамического программирования по подмножествам (маскам). Метод предполагает кодирование множества через битовые последовательности для удобства дальнейших операций. С небольшими наборами легко работать через битовые операции. В частности, кодирование набора тем требует 18 бит. Тогда i-й бит в двоичной записи числа будет отвечать за то, взята ли уже i-я тема (1), или ещё нет (0). В итоге в стандартном 32-битном целом можно хранить все множества тем. Всего получается 2^18 масок, задающих 2^18 подмножеств.
Хранение подмножеств в битах удобно еще и тем, что стандартные операции битового И (AND) позволяют пересекать множества, а битового ИЛИ (OR) — объединять множества.
Поскольку в постановке задачи есть ограничение, требующее, чтобы была представлена задача каждого уровня сложности, введем еще одно измерение — массив dp[i][j]. Он будет определять, можно ли, взяв по задаче из первых i уровней сложности, набрать множество тем, задаваемое битовой маской j, без пересечения по темам между взятыми задачами.
Далее переходим на уровень выше (i+1), выбирая среди задач сложности i+1 ту, битовая маска тем которой не пересекается с маской состояния, и так до тех пор, пока не дойдем до ситуации, когда все темы будут исчерпаны (правый верхний угол матрицы). Если таких задач сложности i+1 найти не удалось, значит, ответ — Impossible.
for (int[] t : P) { Arrays.fill(t, -1);} // инициализуем все “-1”
P[0][0] = -2; // начинаем с нуля
for (int i = 0; i < tl.length; ++i) { // по всем уровням сложности
for (Task t : tl[i]) { // по всем задачам
for (int mask = 0; mask < P[i].length; ++mask) { // по всем наборам тем
if ((mask & t.mask) == 0 && P[i][mask] != -1) { // если пометка есть и пересечения по темам нет
// ставим пометку в виде индекса задачи
dp[i + 1][mask | t.mask] = t.num;
}
}
}
}
// если в правом верхнем углу матрицы пометки нет
if (dp[d][(1 << m) - 1] == -1) {
out.println("Impossible"); // …нет и решения
} else {
out.println("OK");
int[] ans = new int[d];
int mask = (1 << m) - 1; // начинаем с правого верхнего угла
for (int i = d; i > 0; --i) {
ans[i - 1] = dp[i][mask] + 1;
mask ^= mm[dp[i][mask]];
}
for (int i : ans) { out.print(i + " "); }
}
Всего было направлено на проверку 407 решений, из них правильных всего 115 (28%). 12% участников Russian Code Cup QR2 справились с этой задачей. Первое решение пришло от Никиты Иоффе через 16 минут после начала раунда.
«Текстовый редактор»
В задаче на входе мы получаем позицию и вводимый в эту позицию символ (алфавитный + скобки), на выходе — при каждом вводе скобки мы должны возвращать позицию введенной ранее парной скобки, или −1, если парной скобки не существует. Необходимо корректно обрабатывать ситуацию, что входные данные могут поменять одну ранее добавленную скобку на другую, а также то, что символов и скобок может быть очень много (размер текста — 100000).
Несмотря на довольно простую постановку, эта задача является самой сложной из представленных. Здесь основная трудность в том, что размер текста может быть большим, и использовать последовательное сканирование и прямой подсчет неэффективно.
Для решения задачи используется структура данных «Дерево отрезков». Она позволяет быстро выполнять операции изменения любого элемента на новое значение и быстро вычислять некоторые функции (сумму, минимум, максимум) на произвольном отрезке от i до j. «Быстро» в данном случае означает за О (log n), то есть значительно быстрее, чем при последовательном просмотре.
С алгоритмом, реализующим концепцию дерева отрезков, можно ознакомиться здесь: e-maxx.ru/algo/segment_tree .
В нашем случае в дереве отрезков мы будем хранить текущую «глубину» скобочной последовательности для каждой позиции в тексте. Она будет храниться в листьях дерева, в вершинах будут храниться расчетные минимумы, в корне дерева — абсолютный минимум по всему дереву.
Соответственно, поиск закрывающей скобки сводится к поиску элемента справа (для открывающей скобки) или слева (для закрывающей), имеющей ту же глубину. Вместо последовательного просмотра тут будет спуск по дереву — по минимумам значений, не превышающих глубину перед открывающей скобкой или после закрывающей.
При вставке скобки необходимо пересчитать все элементы справа от нее, а также все минимумы в вершинах, охватывающих эти элементы. Здесь может быть использовано т.н. «запаздывающее» обновление — информация об изменении остается в вершинах и спускается до «листьев» тогда, когда понадобится обращение к ним.
Всего было направлено на проверку 159 решений, из них правильных всего 8 (5%). Менее 1% участников Russian Code Cup QR2 справились с этой задачей. Первое решение пришло от Сергея Федорова через 54 минуты после начала раунда.
Напоминаем, что следующий тур квалификации состоится в это воскресенье, 10 июня, в 11:00. Это последний шанс попасть в полуфинал! Необходима предварительная регистрация. Торопитесь!
Алиев Рауф
директор по исследованиям и образованию
руководитель проекта Russian Code Cup
Mail.Ru Group
Автор: raliev






