Кручинин Дмитрий, Долотов Евгений, Кустикова Валентина, Дружков Павел, Корняков Кирилл
Введение
В настоящее время машинное обучение является активно развивающейся областью научных исследований. Это связано как с возможностью быстрее, выше, сильнее, проще и дешевле собирать и обрабатывать данные, так и с развитием методов выявления из этих данных законов, по которым протекают физические, биологические, экономические и другие процессы. В некоторых задачах, когда такой закон определить достаточно сложно, используют глубокое обучение.
Глубокое обучение (deep learning) рассматривает методы моделирования высокоуровневых абстракций в данных с помощью множества последовательных нелинейных трансформаций, которые, как правило, представляются в виде искусственных нейронных сетей. На сегодняшний день нейросети успешно используются для решения таких задач, как прогнозирование, распознавание образов, сжатие данных и ряда других.
Актуальность темы машинного обучения и, в частности, глубокого обучения подтверждается регулярным появлением статей на данную тему на хабре:
- Deep learning и Caffe на новогодних праздниках.
- Data mining: Инструментарий — Theano.
- Про котиков, собак, машинное обучение и deep learning.
- Еженедельные обзоры наиболее интересных материалов по анализу данных и машинному обучению.
Данная статья посвящена сравнительному анализу некоторых программных инструментов глубокого обучения, коих в последнее время появилось великое множество [1]. К числу таких инструментов относятся программные библиотеки, расширения языков программирования, а также самостоятельные языки, позволяющие использовать готовые алгоритмы создания и обучения нейросетевых моделей. Существующие инструменты глубокого обучения имеют различный функционал и требуют от пользователя разного уровня знаний и навыков. Правильный выбор инструмента — важная задача, позволяющая добиться необходимого результата за наименьшее время и с меньшей затратой сил.
В статье представлен краткий обзор инструментов проектирования и обучения нейросетевых моделей. Основное внимание уделено четырем библиотекам: Caffe, Pylearn2, Torch и Theano. Рассматриваются базовые возможности указанных библиотек, приводятся примеры их использования. Сравнивается качество и скорость работы библиотек при конструировании одинаковых топологий нейросетей для решения задачи классификации рукописных цифр (в качестве обучающей и тестовой выборки используется датасет MNIST). Также делается попытка дать оценку удобства применения рассматриваемых библиотек на практике.
Набор данных MNIST
Далее в качестве исследуемого набора данных будет использоваться база изображений рукописных цифр MNIST (рис. 1). Изображения в данной базе имеют разрешение 28x28 и хранятся в формате оттенков серого. Цифры отцентрированы на изображении. Вся база разбита на две части: тренировочную, состоящую из 50000 изображений, и тестовую — 10000 изображений.

Рис. 1. Примеры изображений цифр в базе MNIST
Программные средства для решения задач глубокого обучения
Существует множество программных средств для решения задач глубокого обучения. В [1] можно найти общее сравнение функциональных возможностей наиболее известных, здесь приведем общую информацию о некоторых из них (таблица 1). Первые шесть программных библиотек реализуют наиболее широкий спектр методов глубокого обучения. Разработчики предоставляют возможности для создания полностью связанных нейросетей (fully connected neural network, FC NN [2]), сверточных нейронных сетей (convolutional neural network, CNN) [3], автокодировщиков (autoencoder, AE) и ограниченных машин Больцмана (restricted Boltzmann machine, RBM) [4]. Необходимо обратить внимание на оставшиеся библиотеки. Несмотря на то, что они обладают меньшей функциональностью, в некоторых случаях их простота помогает достичь большей производительности.
Таблица 1. Возможности программных средств глубокого обучения [1]
| # | Название | Язык | OC | FC NN | CNN | AE | RBM |
| 1 | DeepLearnToolbox | Matlab | Windows, Linux | + | + | + | + |
| 2 | Theano | Python | Windows, Linux, Mac | + | + | + | + |
| 3 | Pylearn2 | Python | Linux, Vagrant | + | + | + | + |
| 4 | Deepnet | Python | Linux | + | + | + | + |
| 5 | Deepmat | Matlab | ? | + | + | + | + |
| 6 | Torch | Lua, C | Linux, Mac OS X, iOS, Android | + | + | + | + |
| 7 | Darch | R | Windows, Linux | + | — | + | + |
| 8 | Caffe | C++, Python, Matlab | Linux, OS X | + | + | — | — |
| 9 | nnForge | С++ | Linux | + | + | — | — |
| 10 | CXXNET | С++ | Linux | + | + | — | — |
| 11 | Cuda-convnet | С++ | Linux, Windows | + | + | — | — |
| 12 | Cuda CNN | Matlab | Linux, Windows | + | + | — | — |
Основываясь на приведенной в [1] информации и рекомендациях специалистов, для дальнейшего рассмотрения выбраны четыре библиотеки: Theano, Pylearn2 — одни из самых зрелых и функционально полных библиотек, Torch и Caffe — широко используемые сообществом. Каждая библиотека рассматривается по следующему плану:
- Краткая справочная информация.
- Технические особенности (ОС, язык программирования, зависимости).
- Функциональные возможности.
- Пример формирования сети типа логистическая регрессия.
- Обучение и использование построенной модели для классификации.
После рассмотрения перечисленных библиотек проводится их сравнение на ряде тестовых конфигураций сетей.
Библиотека Caffe
Разработка Caffe ведется с сентября 2013 г. Начало разработки положил Yangqing Jia во время его обучения в калифорнийском университете в Беркли. С указанного момента Caffe активно поддерживается Центром Зрения и Обучения Беркли (The Berkeley Vision and Learning Center, BVLC) и сообществом разработчиков на GitHub. Библиотека распространяется под лицензией BSD 2-Clause.
Caffe реализована с использованием языка программирования C++, имеются обертки на Python и MATLAB. Официально поддерживаемые операционные системы — Linux и OS X, также имеется неофициальный порт на Windows. Caffe использует библиотеку BLAS (ATLAS, Intel MKL, OpenBLAS) для векторных и матричных вычислений. Наряду с этим, в число внешних зависимостей входят glog, gflags, OpenCV, protoBuf, boost, leveldb, nappy, hdf5, lmdb. Для ускорения вычислений Caffe может быть запущена на GPU с использованием базовых возможностей технологии CUDA или библиотеки примитивов глубокого обучения cuDNN.
Разработчики Caffe поддерживают возможности создания, обучения и тестирования полностью связанных и сверточных нейросетей. Входные данные и преобразования описываются понятием слоя. В зависимости от формата хранения могут использоваться следующие типы слоев исходных данных:
- DATA — определяет слой данных в формате leveldb и lmdb.
- HDF5_DATA — слой данных в формате hdf5.
- IMAGE_DATA — простой формат, который предполагает, что в файле приведен список изображений с указанием метки класса.
- и другие.
Преобразования могут быть заданы с помощью слоев:
- INNER_PRODUCT — полностью связанный слой.
- CONVOLUTION — сверточный слой.
- POOLING — слой пространственного объединения.
- Local Response Normalization (LRN) — слой локальной нормализации.
Наряду с этим, при формировании преобразований могут использоваться различные функции активации.
- Положительная часть (Rectified-Linear Unit, ReLU).
- Сигмоидальная функция (SIGMOID).
- Гиперболический тангенс (TANH).
- Абсолютное значение (ABSVAL).
- Возведение в степень (POWER).
- Функция биноминального нормального логарифмического правдоподобия (binomial normal log likelihood, BNLL).
Последний слой нейросетевой модели должен содержать функцию ошибки. В библиотеке имеются следующие функции:
- Среднеквадратичная ошибка (Mean-Square Error, MSE).
- Краевая ошибка (Hinge loss).
- Логистическая функция ошибки (Logistic loss).
- Функция прироста информации (Info gain loss).
- Сигмоидальная кросс-энтропия (Sigmoid cross entropy loss).
- Softmax-функция. Обобщает сигмоидальную кросс-энтропию на случай количества классов больше двух.
В процессе обучения моделей применяются различные методы оптимизации. Разработчики Caffe предоставляют реализацию ряда методов:
- Стохастический градиентный спуск (Stochastic Gradient Descent, SGD) [6].
- Алгоритм с адаптивной скоростью обучения (adaptive gradient learning rate algorithm, AdaGrad) [7].
- Ускоренный градиентный спуск Нестерова (Nesterov’s Accelerated Gradient Descent, NAG) [8].
В библиотеке Caffe топология нейросетей, исходные данные и способ обучения задаются с помощью конфигурационных файлов в формате prototxt. Файл содержит описание входных данных (тренировочных и тестовых) и слоев нейронной сети. Рассмотрим этапы построения таких файлов на примере сети “логистическая регрессия” (рис. 2). Далее будем считать, что файл называется linear_regression.prototxt, и он размещается в директории examples/mnist.

Рис. 2. Структура нейронной сети
- Зададим имя сети.
name: "LinearRegression" - В качестве обучающего множества используется база данных MNIST, хранящаяся в формате lmdb. Для работы с форматами lmdb или leveldb используется слой типа “DATA”, в котором необходимо указать некоторые параметры, описывающие входные данные (data_param): путь до данных на жестком диске (source), тип данных (backend), размер выборки (batch_size). Также с данными можно производить различные преобразования (transform_param). Например, можно произвести нормировку изображения, умножив все значения на 0.00390625 (число, обратное к 255). В параметре top указывается одно или несколько имен, которые будут использованы для идентификации выхода слоя. В данном примере это обработанные изображения (data) и метки классов, которым принадлежат изображения (label).
layers { name: "mnist" type: DATA top: "data" top: "label" data_param { source: "examples/mnist/mnist_train_lmdb" backend: LMDB batch_size: 64 } transform_param { scale: 0.00390625 } } - Определим полносвязный слой (выход каждого нейрона предыдущего слоя связан с входом каждого нейрона последующего слоя). Полносвязный слой в библиотеке Caffe задается с помощью слоя типа INNER_PRODUCT. Имя входных данных указывается с помощью параметра bottom. В данном слое входными данными являются обработанные изображения (data). Количество нейронов в слое определяется автоматичестки (по количеству выходов в предыдушем слое), а количество выходных нейронов указывается с помощью параметра num_output. Результат работы слоя положим по тому же имени, что и имя слоя (ip).
layers { name: "ip" type: INNER_PRODUCT bottom: "data" top: "ip" inner_product_param { num_output: 10 } } - В конце добавим слой, вычисляющий функцию ошибки. Он принимает на вход результат предыдущего полносвязного слоя (ip) и номера классов для каждого изображения (label). После вычислений к результатам работы данного слоя можно обратиться по имени loss.
layers { name: "loss" type: SOFTMAX_LOSS bottom: "ip" bottom: "label" top: "loss" }
Конфигурация сети готова. Далее необходимо определить параметры процедуры обучения в файле формата prototxt (назовем его solver.prototxt). К числу параметров обучения относятся путь к файлу с конфигурацией сети (net), периодичность тестирования во время обучения (test_interval), параметры стохастического градиентного спуска (base_lr, weight_decay и другие), максимальное количество итераций (max_iter), архитектура, на которой будут проводиться вычисления (solver_mode), путь для сохранения обученной сети (snapshot_prefix).
net: "examples/mnist/linear_regression.prototxt"
test_iter: 100
test_interval: 500
base_lr: 0.01
momentum: 0.9
weight_decay: 0.0005
lr_policy: "inv"
gamma: 0.0001
power: 0.75
display: 100
max_iter: 10000
snapshot: 5000
snapshot_prefix: "examples/mnist/linear_regression"
solver_mode: GPU
Обучение выполняется с использованием основного приложения библиотеки. При этом передается определенный набор ключей, в частности, название файла, содержащего описание параметров процедуры обучения.
caffe train --solver=solver.prototxt
После обучения полученную модель можно использовать для классификации изображений, например, с помощью оберток на Python:
- Подключаем библиотеку Caffe. Устанавливаем режим тестирования и указываем архитектуру для выполнения вычислений (CPU или GPU).
import caffe caffe.set_phase_test() caffe.set_mode_cpu() - Создаем нейронную сеть, указывая следующие параметры: MODEL_FILE — конфигурация сети в формате prototxt, PRETRAINED — обученная сеть в формате caffemodel, IMAGE_MEAN — среднее изображение (вычисляется по набору входных изображений и используется для последующей нормализации интенсивности), channel_swap задает цветовую модель, raw_scale — максимальное значение интенсивности, image_dims — разрешение изображения. После чего, загружаем изображение для классификации (IMAGE_FILE).
net = caffe.Classifier(MODEL_FILE, PRETRAINED, IMAGE_MEAN, channel_swap=(0,1,2), raw_scale=255, image_dims=(28, 28)) input_image = caffe.io.load_image(IMAGE_FILE) - Получаем ответ нейросети для выбранного изображения и выводим результаты на экран.
prediction = net.predict([input_image]) print 'prediction shape:', prediction[0].shape print 'predicted class:', prediction[0].argmax()
Таким образом, путем несложных действий можно получить первые результаты экспериментов с глубокими нейросетевыми моделями. Более сложные и подробные примеры можно увидеть на сайте разработчиков.
Библиотека Pylearn2

Pylearn2 — библиотека, разрабатываемая в лаборатории LISA в университете Монреаля с февраля 2011 года. Имеет около 100 разработчиков на GitHub. Библиотека распространяется под лицензией BSD 3-Clause.
Pylearn2 реализована на языке Python, в настоящее время поддерживается операционная система Linux, также возможен запуск на любой операционной системе с использованием виртуальной машины, т.к. разработчики предоставляют сконфигурированную обертку виртуальной среды на базе Vagrant. Pylearn2 является надстройкой над библиотекой Theano. Дополнительно требуются PyYAML, PIL. Для ускорения вычислений Pylearn2 и Theano используют Cuda-convnet, которая реализована на C++/CUDA, что дает значительный прирост в скорости.
В Pylearn2 поддерживается возможность создания полностью связанных и сверточных нейросетей, различных видов автокодировщиков (Contractive Auto-Encoders, Denoising Auto-Encoders) и ограниченных машин Больцмана (Gaussian RBM, the spike-and-slab RBM). Предусмотрены несколько функций ошибки: кросс-энтропия (cross-entropy), логарифмическое правдоподобие (log-likelihood). Имеются следующие методы обучения:
- Пакетный градиентный спуск (Batch Gradient Descent, BGD).
- Стохастический градиентный спуск (Stochastic Gradient Descent, SGD).
- Нелинейный метод сопряженных градиентов (Nonlinear conjugate gradient descent, NCG).
В библиотеке Pylearn2 нейросети задаются с помощью их описания в конфигурационном файле в формате YAML. YAML-файлы являются удобным и быстрым способом сериализации объектов, так как она разработана с использованием методов объектно-ориентированного программирования.
Рассмотрим процедуру формирования YAML-файлов, описывающих структуру нейросети и способ ее обучения, на примере логистической регрессии.
- Определим тренировочное множество. В Pylearn2 уже реализован класс для работы с базой данных MNIST. Тренировку будем проводить на первых 50000 изображений.
!obj:pylearn2.train.Train { dataset: &train !obj:pylearn2.datasets.mnist.MNIST { which_set: 'train', one_hot: 1, start: 0, stop: 50000 }, - Опишем структуру сети. Для этого используем класс, реализующий логистическую регрессию. Достаточно только указать необходимые параметры. Количество входных нейронов в полностью связанном слое (nvis) – 784 (по количеству пикселей в изображении), выходных (n_classes) – 10 (по количеству классов объектов), начальные веса (iranges) определим нулями.
model: !obj:pylearn2.models.softmax_regression.SoftmaxRegression { n_classes: 10, irange: 0., nvis: 784, }, - Выберем алгоритм обучения нейросети и его параметры. Для обучения выберем метод пакетного градиентного спуска (BGD). Параметр batch_size отвечает за размер тренировочной выборки, используемой на каждом шаге градиентного спуска. Установка параметра line_search_mode в значение exhaustive означает, что метод пакетного градиентного спуска (BGD) будет пытаться использовать двоичный поиск для достижения наилучшей точки вдоль направления градиента, что ускоряет сходимость градиентного спуска. В ходе обучения будем отслеживать результаты классификации на тренировочной, валидационной (изображения с 50000 по 60000) и тестовой выборках. Критерий остановки – максимальное количество итераций оптимизации.
algorithm: !obj:pylearn2.training_algorithms.bgd.BGD { batch_size: 128, line_search_mode: 'exhaustive', monitoring_dataset: { 'train' : *train, 'valid' : !obj:pylearn2.datasets.mnist.MNIST { which_set: 'train', one_hot: 1, start: 50000, stop: 60000 }, 'test' : !obj:pylearn2.datasets.mnist.MNIST { which_set: 'test', one_hot: 1, } }, termination_criterion: !obj:pylearn2.termination_criteria.And { criteria: [ !obj:pylearn2.termination_criteria.EpochCounter { max_epochs: 150 }, ] } }, - Для дальнейшего использования обученной модели необходимо сохранить полученный результат. Отметим, что модель сохраняется в формате pkl.
extensions: [ !obj:pylearn2.train_extensions.best_params.MonitorBasedSaveBest { channel_name: 'valid_y_misclass', save_path: "%(save_path)s/softmax_regression_best.pkl" }, ]
Таким образом, подготовлена конфигурация сети и определена необходимая инфраструктура для обучения и классификации, которые выполняются посредством вызова соответствующего Python-скрипта. Для обучения необходимо выполнить следующую командную строку:
python train.py <файл с конфигурацией сети>.yamlБолее сложные и подробные примеры можно увидеть на официальном сайте или в репозитории.
Библиотека Torch

Torch — библиотека для научных вычислений с широкой поддержкой алгоритмов машинного обучения. Разрабатывается Idiap Research Institute, New York University и NEC Laboratories America, начиная с 2000г., распространяется под лицензией BSD.
Библиотека реализована на языке Lua с использованием C и CUDA. Быстрый скриптовый язык Lua в совокупности с технологиями SSE, OpenMP, CUDA позволяют Torch показывать неплохую скорость по сравнению с другими библиотеками. На данный момент поддерживаются операционные системы Linux, FreeBSD, Mac OS X. Основные модули также работают и на Windows. В зависимостях Torch находятся пакеты imagemagick, gnuplot, nodejs, npm и другие.
Библиотека состоит из набора модулей, каждый из которых отвечает за различные стадии работы с нейросетями. Так, например, модуль nn обеспечивает конфигурирование нейросети (определению слоев, и их параметров), модуль optim содержит реализации различных методов оптимизации, применяемых для обучения, а gnuplot предоставляет возможность визуализации данных (построение графиков, показ изображений и т.д.). Установка дополнительных модулей позволяет расширить функционал библиотеки.
Torch позволяет создавать сложные нейросети с помощью механизма контейнеров. Контейнер — это класс, объединяющий объявленные компоненты нейросети в одну общую конфигурацию, которая в дальнейшем может быть передана в процедуру обучения. Компонентом нейросети могут быть не только полносвязные или сверточные слои, но и функции активации или ошибки, а также готовые контейнеры. Torch позволяет создавать следующие слои:
- Полносвязный слой (Linear).
- Функции активации: гиперболический тангенс (Tanh), выбор минимального (Min) или максимального (Max), softmax-функция (SoftMax) и другие.
- Сверточные слои: свертка (Convolution), прореживание (SubSampling), пространственное объединение (MaxPooling, AveragePooling, LPPooling), разностная нормализация (SubtractiveNormalization).
Функции ошибки: средне-квадратичная ошибка (MSE), кросс-энтропия (CrossEntropy) и т.д.
При обучении могут использоваться следующие методы оптимизации:
- Стохастический градиентный спуск (SGD),
- Усредненный стохастический градиентный спуск (Averaged SGD) [9].
- Алгоритм Бройдена – Флетчера – Гольдфарба – Шанно (L-BFGS) [10].
- Метод сопряженных градиентов (Conjugate Gradient, CG).
Рассмотрим процесс конфигурирования нейронной сети в Torch. Сначала необходимо объявить контейнер, затем добавить в него слои. Порядок добавления слоев важен, т.к. выход (n-1)-го слоя будет входом n-го.
regression = nn.Sequential()
regression:add(nn.Linear(784,10))
regression:add(nn.SoftMax())
loss = nn.ClassNLLCriterion()
Использование и обучение нейросети:
- Загрузка входных данных X. Функция torch.load(path_to_ready_dset) позволяет загрузить подготовленный заранее датасет в текстовом или бинарном формате. Как правило, это Lua-таблица состоящая из трёх полей: размер, данные и метки. В случае если готового датасета нет, можно воспользоваться стандартными функциями языка Lua (например, io.open(filename [, mode])) или функциями из пакетов библиотеки Torch (например, image.loadJPG(filename)).
- Определение ответа сети для входных данных X:
Y = regression:forward(X) - Вычисление функции ошибки E = loss(Y,T), в нашем случае это функция правдоподобия.
E = loss:forward(Y,T) - Просчет градиентов согласно алгоритму обратного распространения.
dE_dY = loss:backward(Y,T) regression:backward(X,dE_dY)
Теперь соберем все воедино. Для того чтобы обучить нейросеть в библиотеке Torch, необходимо написать собственный цикл обучения. В нем объявить специальную функцию (замыкание), которая будет вычислять ответ сети, определять величину ошибки и пересчитывать градиенты, и передать это замыкание в функцию градиентного спуска для обновления весов сети.
-- Создаём специальные переменные: веса нейросети и их градиенты
w, dE_dw = regression:getParameters()
local eval_E = function(w)
dE_dw:zero() -- Обновляем градиенты
local Y = regression:forward(X)
local E = loss:forward(Y,T)
local dE_dY = loss:backward(Y,T)
regression:backward(X,dE_dY)
return E, dE_dw
end
-- Затем в цикле обучения вызываем
optim.sgd(eval_E, w, optimState)
где optimState — параметры градиентного спуска (learningRate, momentum, weightDecay и пр.). Полностью цикл обучения можно посмотреть здесь.
Несложно видеть, что процедура объявления, как и процедура обучения, занимает менее 10 строк кода, что говорит о простоте использования библиотеки. При этом библиотека позволяет работать с нейросетями на достаточно низком уровне.
Сохранение и загрузка натренированной сети осуществляется с помощью специальных функций:
torch.save(path, regression)
net = torch.load(path)
После загрузки сеть может быть использована для классификации или дополнительной тренировки. Если необходимо узнать, к какому классу принадлежит элемент sample, то достаточно выполнить проход по сети и вычислить выход:
result = net:forward(sample)
Более сложные примеры можно найти в обучающих материалах к библиотеке.
Библиотека Theano

Theano — это расширение языка Python, позволяющее эффективно вычислять математические выражения, содержащие многомерные массивы. Библиотека получила свое название в честь имени жены древнегреческого философа и математика Пифагора — Феано (или Теано). Theano разработана в лаборатории LISA для поддержки быстрой разработки алгоритмов машинного обучения.
Библиотека реализована на языке Python, поддерживается на операционных системах Windows, Linux и Mac OS. В состав Theano входит компилятор, который переводит математические выражения, написанные на языке Python в эффективный код на C или CUDA.
Theano предоставляет базовый набор инструментов для конфигурации нейросетей и их обучения. Возможна реализация многослойных полностью связанных сетей (Multi-Layer Perceptron), сверточных нейросетей (CNN), рекуррентных нейронных сетей (Recurrent Neural Networks, RNN), автокодировщиков и ограниченных машин Больцмана. Также предусмотрены различные функции активации, в частности, сигмоидальная, softmax-функция, кросс-энтропия. В ходе обучения используется пакетный градиентный спуск (Batch SGD).
Рассмотрим конфигурацию нейросети в Theano. Для удобства реализуем класс LogisticRegression (рис. 3), в котором будут содержаться переменные — обучаемые параметры W, b и функции для работы с ними — подсчет ответа сети (y = softmax(Wx + b)) и функция ошибки. Затем для тренировки нейросети создаем функцию train_model. Для нее необходимо описать методы, определяющие функцию ошибки, правило вычисления градиентов, способ изменения весов нейросети, размер и местоположение mini-batch выборки (сами изображения и ответы для них). После определения всех параметров функция компилируется и передается в цикл обучения.

Рис. 3. Схема класса для реализации нейронной сети в Theano
class LogisticRegression(object):
def __init__(self, input, n_in, n_out):
# y = W * x + b
# объявляем переменные, определяем тип, количество входов и выходов
self.W = theano.shared(
# инициализируем начальные веса нулями
value=numpy.zeros((n_in, n_out), dtype=theano.config.floatX), name='W', borrow=True)
self.b = theano.shared(value=numpy.zeros((n_out,), dtype=theano.config.floatX), name='b', borrow=True)
# добавляем функцию активации softmax, выход сети - переменная y_pred
self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W) + self.b)
self.y_pred = T.argmax(self.p_y_given_x, axis=1)
self.params = [self.W, self.b]
# определяем функцию ошибки
def negative_log_likelihood(self, y):
return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]), y])
# x - подается на вход сети
# набор изображений (minibatch) располагается по строкам в матрице x
# y - ответ сети на каждый семпл
x = T.matrix('x')
y = T.ivector('y')
# создаем модель логистической регрессии каждое MNIST изображение имеет размер 28*28
classifier = LogisticRegression(input=x, n_in=28 * 28, n_out=10)
# значение функции ошибки, которое мы пытаемся минимизировать в течение обучения
cost = classifier.negative_log_likelihood(y)
# чтобы посчитать градиенты, необходимо вызвать функцию Theano - grad
g_W = T.grad(cost=cost, wrt=classifier.W)
g_b = T.grad(cost=cost, wrt=classifier.b)
# определяем правила обновления весов нейросети
updates = [(classifier.W, classifier.W - learning_rate * g_W), (classifier.b, classifier.b - learning_rate * g_b)]
# компилируем функцию тренировки, в дальнейшем она будет вызываться в цикле обучения
train_model = theano.function(
inputs=[index], outputs=cost, updates=updates,
givens={
x: train_set_x[index * batch_size: (index + 1) * batch_size],
y: train_set_y[index * batch_size: (index + 1) * batch_size]
}
)
Для быстрого сохранения и загрузки параметров нейросети можно использовать функции из пакета cPickle:
import cPickle
save_file = open('path', 'wb')
cPickle.dump(classifier.W.get_value(borrow=True), save_file, -1)
cPickle.dump(classifier.b.get_value(borrow=True), save_file, -1)
save_file.close()
file = open('path')
classifier.W.set_value(cPickle.load(save_file), borrow=True)
classifier.b.set_value(cPickle.load(save_file), borrow=True)
Несложно видеть, что процесс создания модели и определения ее параметров требует написания объемного и шумного кода. Библиотека является низкоуровневой. Нельзя не отметить ее гибкость, а также наличие возможности реализации и использования собственных компонент. На официальном сайте библиотеки имеется большое количество обучающих материалов на разные темы.
Сравнение библиотек на примере задачи классификации рукописных цифр
Тестовая инфраструктура
В ходе экспериментов по оценке производительности библиотек использована следующая тестовая инфраструктура:
- Ubuntu 12.04, Intel Core i5-3210M @ 2.5GHz (CPU эксперименты).
- Ubuntu 14.04, Intel Core i5-2430M @ 2.4GHz + NVIDIA GeForce GT 540M (GPU эксперименты).
- GCC 4.8, NVCC 6.5.
Топологии сетей и параметры обучения
Вычислительные эксперименты проводились на полносвязной и сверточной нейронных сетях следующей структуры:
- Трехслойная полносвязная нейронная сеть (MLP, рис. 4):
- 1st layer – FC (in: 784, out: 392, activation: tanh).
- 2d layer – FC (in: 392, out: 196, activation: tanh).
- 3d layer – FC (in: 196, out: 10, activation: softmax).
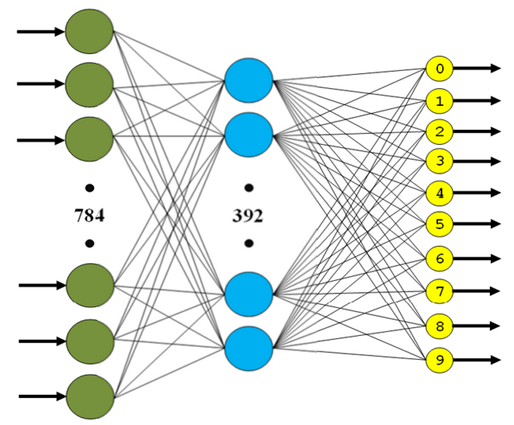
Рис. 4. Структура трехслойной полносвязной сети
- Сверточная нейронная сеть (CNN, рис. 5):
- 1st layer – convolution (in filters: 1, out filters: 28, size: 5x5, stride: 1x1).
- 2d layer – max-pooling (size: 3x3, stride: 3x3).
- 3d layer – convolution (in filters: 28, out filters: 56, size: 5x5, stride 1x1).
- 4th layer – max-pooling (size: 2x2, stride: 2x2).
- 5th layer – FC (in: 224, out: 200, activation: tanh).
- 6th layer – FC (in: 200, out: 10, activation: softmax).
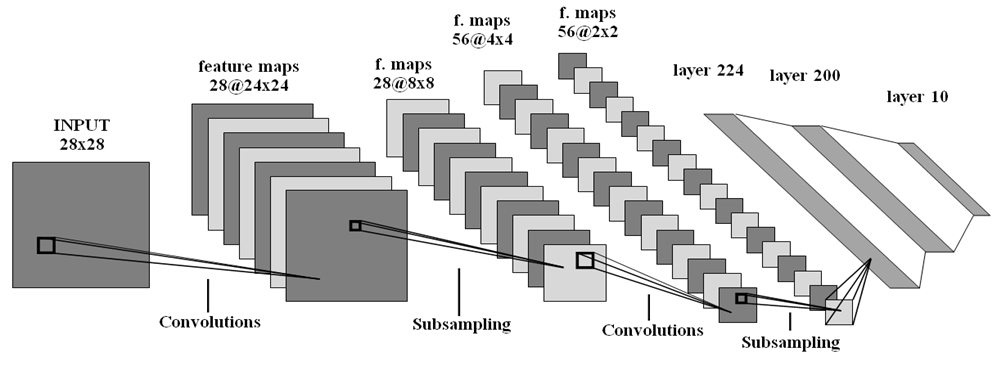
Рис. 5. Структура сверточной нейронной сети
Все веса инициализировались случайным образом согласно равномерному закону распределения в диапазоне (−6/(n_in + n_out), 6/(n_in + n_out)), где n_in, n_out – количество нейронов на входе и выходе слоя соответственно. Параметры стохастического градиентного спуска (SGD) выбраны, равными следующим значениям: learning rate — 0.01, momentum — 0.9, weight decay — 5e-4, batch size — 128, максимальное число итераций — 150.
Результаты экспериментов
Время обучения нейронных сетей, описанных ранее (рис. 4, 5) с помощью четырех рассмотренных библиотек, представлено ниже (рис. 6). Легко заметить, что Pylearn2 показывает худшую производительность (как на CPU, так и на GPU) по сравнению с другими библиотеками. Что же касается остальных, время обучения сильно зависит от структуры сети. Лучший результат среди реализаций сетей, запущенных на CPU, показала библиотека Torch (причем на CNN она обогнала саму себя же, запущенную на GPU). Среди GPU-реализаций наилучший результат (на обеих сетях) показала библиотека Caffe. В целом от использования Caffe остались только положительные впечатления.
CPU реализации (см. инфраструктуру):
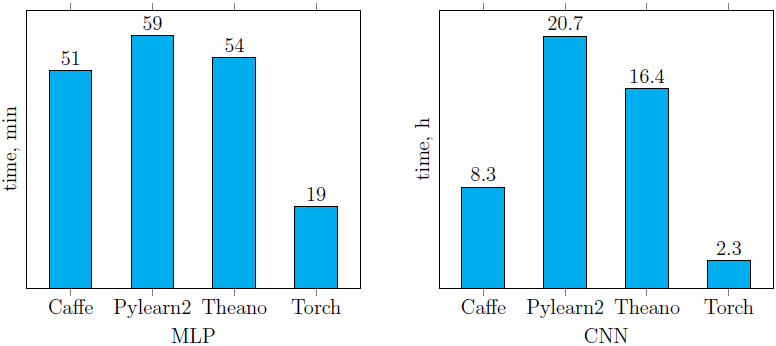
GPU реализации (см. инфраструктуру):
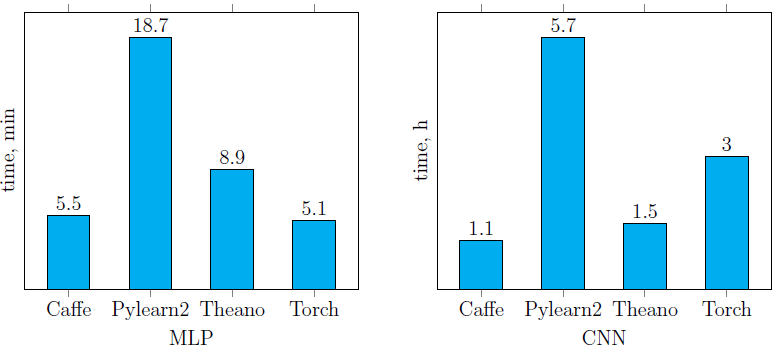
Рис. 6. Время обучения сетей MLP и CNN, описанных в предыдущем пункте
Что же касается времени классификации одного изображения на CPU с помощью обученных моделей (рис. 7), то несложно видеть, что библиотека Torch оказалась вне конкуренции на обеих тестовых нейросетях. Немного от нее отстала Caffe на CNN, которая при этом показала худшее время классификации на MLP.
CPU реализации (см. инфраструктуру):
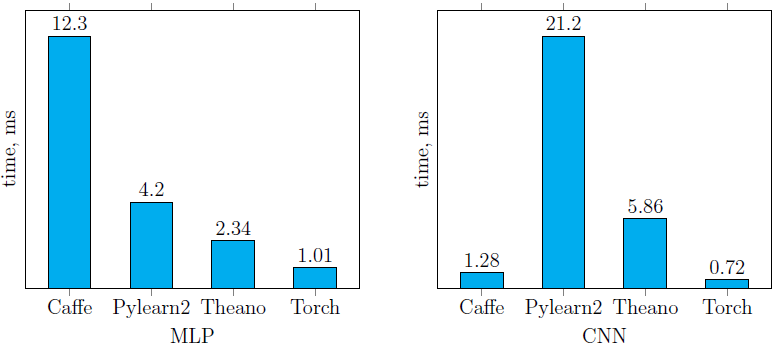
Рис. 7. Время классификации одного изображения с помощью обученных сетей MLP и CNN
Если обратиться к точности классификации, то на сети MLP оно выше 97.4%, а CNN — ~99% для всех библиотек (таблица 2). Полученные значения точности несколько ниже приведенных на сайте MNIST на тех же структурах нейросетей. Небольшие отличия обусловлены различиями в настройках начальных весов сетей и параметрах методов оптимизации, применяемых в процессе обучения. Собственно, цели достижения максимальных значений точности и не было, скорее необходимо было построить идентичные структуры сетей и задать максимально схожие параметры обучения.
Таблица 2. Среднее значение и дисперсия показателей точности классификации по 5 экспериментам
| Caffe | Pylearn2 | Theano | Torch | |||||
| Точность, % | Дисперсия | Точность, % | Дисперсия | Точность, % | Дисперсия | Точность, % | Дисперсия | |
| MLP | 98.26 | 0.0039 | 98.1 | 0 | 97.42 | 0.0023 | 98.19 | 0 |
| CNN | 99.1 | 0.0038 | 99.3 | 0 | 99.16 | 0.0132 | 99.4 | 0 |
Сравнение выбранных библиотек
На основании проведенного исследования функционала библиотек, а также анализа производительности на примере задачи классификации рукописных цифр дана оценка каждой из них по шкале от 1 до 3 по следующим критериям:
- Скорость обучения отражает время обучения нейросетевых моделей, рассмотренных на этапе проведения экспериментов.
- Скорость классификации отражает время классификации одного изображения.
- Удобство использования — критерий, который позволяет оценить время, затраченное на изучение библиотеки.
- Гибкость настройки связей между слоями, установки параметров методов, а также наличие различных способов обработки данных.
- Объем функционала — наличие реализации типовых методов глубокого обучения (полностью связанных сетей, сверточных нейросетей, автокодировщиков, ограниченных машин Больцмана, различных методов оптимизации и функций ошибки).
- Наличие и удобство использования документации и обучающих материалов
Рассмотрим оценки, полученные по каждому критерию, расставим места каждой библиотеке от первого до третьего (таблица 3). Согласно результатам вычислительных экспериментов с точки зрения скорости работы наиболее предпочтительной является библиотека Caffe (рис. 6). При этом она же оказалась наиболее удобной в использовании. С позиции гибкости библиотека Theano показала наилучшие результаты. По функциональным возможностям наиболее полной является Pylearn2, но ее использование осложнено необходимостью понимания внутреннего устройства (формирование YAML-файлов требует этого). Наиболее подробный и понятный материал для изучения предоставляют разработчики Torch. Показав средние показатели по каждому критерию в отдельности, именно она и выиграла в рейтинге рассмотренных библиотек.
Таблица 3. Результаты сравнения библиотек (места от 1 до 3 по каждому критерию)
| Скорость обучения | Скорость классификации | Удобство | Гибкость | Функционал | Документация | Сумма | |
| Caffe | 1 | 2 | 1 | 3 | 3 | 2 | 12 |
| Pylearn2 | 3 | 3 | 2 | 3 | 1 | 3 | 15 |
| Torch | 2 | 1 | 2 | 2 | 2 | 1 | 10 |
| Theano | 2 | 2 | 3 | 1 | 2 | 2 | 12 |
Заключение
Подводя итог, можно сказать, что наиболее зрелой является библиотека Torch. При этом библиотеки Caffe и Theano не уступают ей по многим критериям (таблица 3), поэтому нельзя исключать возможность их последующего использования. В дальнейшем для исследования применимости методов глубокого обучения к задачам детектирования лиц, пешеходов и автомобилей планируется применять библиотеки Caffe и Torch.
Работа выполнена в лаборатории «Информационные технологии» факультета ВМК ННГУ им. Н.И. Лобачевского при поддержке компании Itseez.
Использованные источники
- Kustikova, V.D., Druzhkov, P.N.: A Survey of Deep Learning Methods and Software for Image Classification and Object Detection. In: Proc. of the 9th Open German-Russian Workshop on Pattern Recognition and Image Understanding. (2014)
- Hinton, G.E.: Learning Multiple Layers of Representation. In: Trends in Cognitive Sciences. Vol. 11. pp. 428-434. (2007)
- LeCun, Y., Kavukcuoglu, K., Farabet, C.: Convolutional networks and applications in vision. In: Proc. of the IEEE Int. Symposium on Circuits and Systems (ISCAS). pp. 253-256. (2010)
- Hayat, M., Bennamoun, M., An, S.: Learning Non-Linear Reconstruction Models for Image Set Classification. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. (2014)
- Restricted Boltzmann Machines (RBMs), www.deeplearning.net/tutorial/rbm.html.
- Bottou, L.: Stochastic Gradient Descent Tricks. Neural Networks: Tricks of the Trade, research.microsoft.com/pubs/192769/tricks-2012.pdf.
- Duchi, J., Hazan, E., Singer, Y.: Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. In: The Journal of Machine Learning Research. (2011)
- Sutskever, I., Martens, J., Dahl, G., Hinton, G.: On the Importance of Initialization and Momentum in Deep Learning. In: Proc. of the 30th Int. Conf. on Machine Learning. (2013)
- Усредненный стохастический градиентный спуск (ASGD), research.microsoft.com/pubs/192769/tricks-2012.pdf.
- Алгоритм Бройдена-Флетчера-Гольдфарба-Шанно, en.wikipedia.org/wiki/Limited-memory_BFGS.
Автор: KustikovaV




![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс] Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75)

