Lock-free структуры данных. Concurrent maps: деревья

Это последняя, на сегодняшний день, статья из цикла про внутреннее устройство конкурентных ассоциативных контейнеров. В предыдущих статьях рассматривались hash map, был построен алгоритм lock-free ordered list и контейнеры на его основе. За бортом остался один важный тип структур данных — деревья. Пришло время немного рассказать и о них.

Исследования, посвященные алгоритмам конкурентных деревьев, не требующих внешней синхронизации доступа к ним, начались довольно давно — в 70-х годах прошлого века, — и были инициированы развитием СУБД, поэтому касались в основном оптимизации страничных деревьев (B-tree и его модификации).

Развитие lock-free подхода в начале 2000-х не прошло мимо алгоритмов деревьев, но лишь недавно, в 2010-х годах, появилось множество действительно интересных работ по конкурентным деревьям. Алгоритмы деревьев довольно сложны, поэтому исследователям потребовалось время — порядка 10 лет — на их lock-free/non-blocking адаптацию. В данной статье мы рассмотрим самый простой случай — обычное бинарное дерево, даже не самобалансирующееся.

В чем практический смысл обычного бинарного дерева, спросит читатель, ведь все мы знаем, что для упорядоченных данных такое дерево вырождается в линейный список со сложностью поиска O(N)? Основной смысл в том, чтобы апробировать подходы на простой структуре данных. Кроме того, для случайных данных бинарное дерево подходит довольно хорошо, обеспечивая сложность O(log N), а его внутренняя простота является залогом высокой эффективности. Так что тут все зависит от задачи, где такое дерево используется.

Для начала — ретроспективный взгляд на проблему построения lock-free/non-blocking деревьев. После того, как были найдены довольно эффективные lock-free алгоритмы для очередей и списков, появились работы по lock-free самобалансирующимся деревьям — AVL tree, Red-Black tree. Псевдокод этих алгоритмов был сложен, — сложен настолько, что я бы не взялся его реализовывать, так как мне непонятно, например, как к ним применить схемы управления памятью (Hazard Pointer, RCU или что-то ещё), – алгоритмы полагались на garbage collector (GC) языка, обычно Java. Кроме того, я бы не стал воплощать алгоритм, использующий примитив CAS (compare-and-swap) для поиска ключа в дереве, — CAS слишком тяжел для этого. Да и вообще, несмотря на формальное доказательство корректности такого алгоритма (при наличии GC, — эта оговорка существенна, отсутствие GC может нарушить доказательство), его сложность, наличие множества граничных случаев, казались мне непреодолимыми в свете отладки.

Видимо, не только меня пугала сложность и, по сообщениям разработчиков, неэффективность получающихся lock-free алгоритмов для деревьев. Поэтому в начале 2010-х годов акценты в разработке алгоритмов несколько сместились: вместо того, чтобы обеспечить lock-free любыми средствами, стало появляться много работ, где во главу угла ставилась эффективность операции поиска по дереву. Действительно, деревья применяются в основном в задачах поиска (считается, что поиск — это 70 — 90% операций), и именно поиск должен быть быстрым. Поэтому появились non-blocking алгоритмы, в которых поиск является lock-free, а вставка/удаление могут быть блокируемыми на уровне группы узлов (fine-grained locking) — либо явно с помощью мьютексов, либо неявно с использованием флажков и т.п., то есть по сути это spinning. Такой подход дал менее сложные и более понятные алгоритмы, один из которых мы и рассмотрим.

Binary search tree

Будем рассматривать дерево, в котором данные расположены в листьях, внутренние узлы являются маршрутными и содержат только ключи:

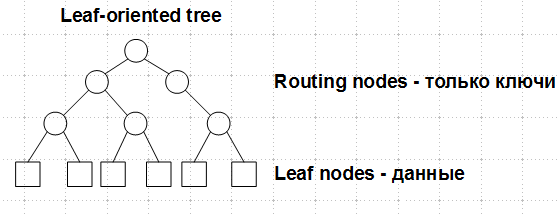
Это так называемое leaf-oriented tree. Наличие искомого ключа во внутреннем узле не говорит о том, что ключ существует в дереве, — только листья содержат ключи и соответствующие им данные, внутренние узлы могут содержать удаленные ключи.

В таком дереве каждый узел имеет ровно двух потомков. Вставка в такое дерево всегда порождает один лист и один внутренний узел, при удалении ключа удаляется один лист и один внутренний узел, его родитель. Никакой балансировки не предусмотрено.

Рассмотрим, какие неожиданности нас ждут при выполнении конкурирующих операций. Пусть имеется некое дерево и потоки A и B выполняют удаление ключей 15 и 27 соответственно:

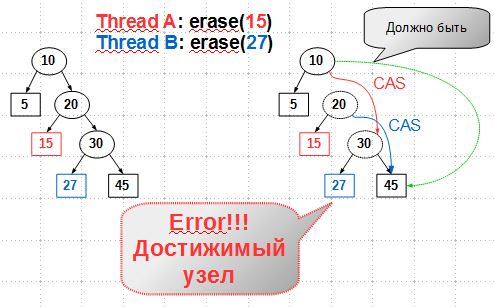
Поток A для удаления ключа 15 должен удалить лист с этим ключом и его родителя — внутренний узел с ключом 20. Для этого он изменяет правую ссылку у своего деда — узла 10 – с узла 20 на узел 30, который является братом удаляемого узла. Так как мы рассматриваем конкурентные деревья, данная операция должна быть выполнена атомарно, то есть с помощью CAS (compare-and-swap).

В это же время поток B удаляет ключ 27. Аналогично вышеописанному, поток B перекидывает CAS'ом правую ссылку узла 20 (деда 27) с 30 на лист 45.

Если эти два действия выполняются параллельно, в результате мы получим достижимый узел 30 и достижимый лист 27, который должен быть удален.

При выполнении конкурирующих удаления и вставки ситуация похожа:

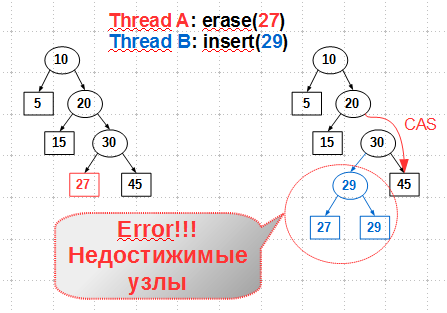
Здесь поток A, удаляющий лист с ключом 27, конкурирует с потоком B, выполняющим вставку нового ключа 29. Для удаления 27 (и его родителя — внутреннего узла 30) поток A перекидывает указатель правого сына узла 20 с 30 на 45. В то же самое время ключ 29 и соответствующий ему внутренний узел 29 вставляются как левый сын узла 30, — в ту же самую позицию, откуда поток A удаляет ключ 27. В результате новый ключ становится недостижимым — утечка памяти.

Очевидно, что примитив CAS сам по себе не может разрулить вышеописанные случаи. Необходимо перед выполнением вставки/удаления каким-то образом помечать узлы, участвующие в операции. В операции вставки участвуют узел-лист и его родитель — внутренний узел. Перед выполнением вставки узел-родитель следует пометить «выполняется вставка», чтобы конкурирующие вcтавки/удаления не смогли выполниться на этом узле. В операции удаления участвуют удаляемый лист, его родитель и родитель его родителя — дед удаляемого листа. Оба внутренних узла — родитель и дед — также должны быть помечены для исключения конкуренции на них.

В этой работе предлагается использовать для каждого внутреннего узла поле состояния State:

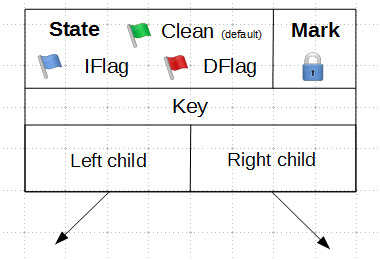
Внутренний узел может находиться в одном из следующих состояний:

• Clean — на узле не выполняется вставок или удалений. Это состояние узла по умолчанию.
• IFlag — в узел выполняется вставка. Таким флагом помечается внутренний узел, у которого хотя бы один сын является листом.
• DFlag — выполняется удаление. Таким флагом помечается внутренний узел-дед удаляемого листа
• Mark — внутренний узел будет удален. Таким флагом помечается родитель удаляемого листа (помним, что в нашем дереве при удалении листа всегда удаляется и его родитель).

Эти состояния взаимоисключающие: каждый узел может находиться только в одном из них. Изменение состояния узла выполняется примитивом CAS.
Вспомним, что нашей основной целью является как можно более эффективная реализация операции поиска ключа в дереве. Как эти состояния влияют на поиск? Очевидно, что операция вставки и соответствующий ей флаг IFlag может быть проигнорирована при поиске: при вставке нет удалений, значит, мы не сможем «зайти в запретную, удаленную зону». А вот флаги DFlag и Mark должны влиять на поиск: при достижении узла с одним из таких флагов поиск должен быть возобновлен с начала (здесь возможны вариации действий, но самое простое — начать поиск заново).

Итак, рассмотрим, как работают эти состояния на примере вставки ключа 29:

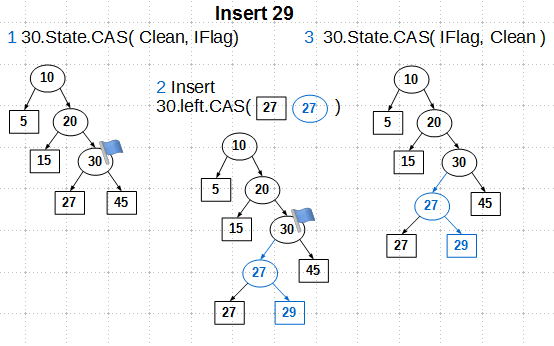
Мы находим узел вставки — это внутренний узел 30. Первым делом мы устанавливаем состояние IFlag узла 30 примитивом CAS. CAS здесь нам гарантирует, что мы перейдем в состояние IFlag только из состояния Clean, что исключает конкурирующие операции, то есть мы становимся эксклюзивными владельцами узла 30. Далее мы создаем внутренний узел 27, задаем ему сыновей — существующий лист 27 и новый 29, — и меняем указатель левого сына узла 30 на вновь созданный внутренний узел 27. Зачем здесь нужен CAS, нельзя ли обойтись обычным атомарным store? Ответ — в оригинальном алгоритме нельзя, в реализации libcds – можно применить атомарный store, об этом мы поговорим позже. И, наконец, третий шаг: снимаем флаг IFlag с узла 30. Здесь также применяется CAS в оригинальном алгоритме, который может быть заменен на атомарный store, если мы откажемся от кое-чего не очень нужного.

Операция удаления с применением флагов State состоит из четырех шагов:

• Помечаем деда удаляемого листа состоянием DFlag с помощью CAS
• Маркируем родителя удаляемого листа состоянием Mark также CAS'ом
• Перекидываем CAS'ом указатель потомка узла-деда
• Снимаем метку DFlag с деда. Здесь используется CAS, но можно использовать и более простой атомарный store при некотором упрощении алгоритма

Заметим, что метку Mark мы не снимаем с узла-родителя удаляемого листа, так как в нашем алгоритме родитель также удаляется и нет смысла в снятии метки с него.

Посмотрим, как работают флаги в случае конкурентного удаления. Без флагов состояния конкурентное удаление ключей 15 и 27 приводило, как мы ранее видели, к достижимости удаленного листа:

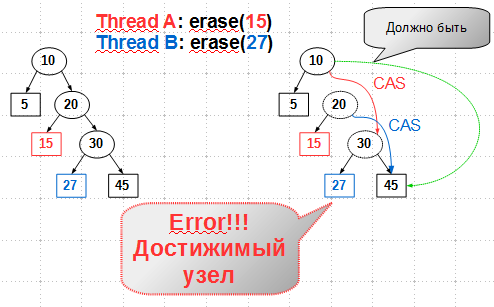
С флагами состояния будем иметь:

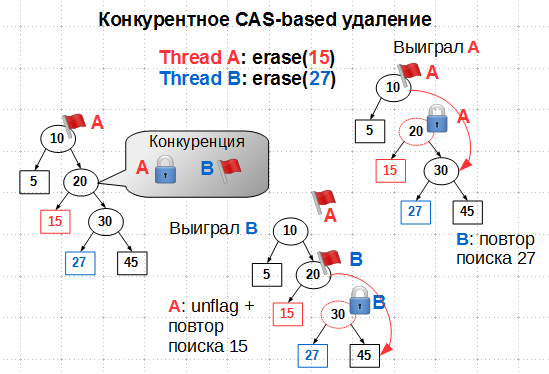
Казалось бы, если поток A поставил флаг DFlag на узле 10, поток B не должен при поиске 27 пройти дальше узла 10. Но у нас операции выполняются параллельно, так что вполне возможно, что поток B успел прошмыгнуть узел 10 до того, как его пометили флагом DFlag. Далее на узле 20 возникает конкуренция: поток A хочет пометить его флагом Mark, поток B – флагом DFlag. Так как установка состояния узла производится атомарным CAS от состояния Clean, только один из потоков выиграет это сражение. Если выигрывает поток A, то есть если он успел пометить 20 флагом Mark, поток B начинает поиск удаляемого узла 27 с начала, а A удаляет 15 и затем снимает флаг DFlag с 10. Если же выигрывает B, пометив 20 флагом DFlag, поток A должен снять свою метку с 10 и повторить поиск узла 15. В обоих случаях удаление ключей выполняется в конце концов успешно и без нарушения структуры дерева.

Как видно, флаги состояния играют роль внутренних мьютексов, обеспечивающих эксклюзивный доступ к удаляемым узлам. Осталось прояснить некие намеки насчет допустимости замены примитива CAS на атомарный store при снятии флагов, то есть при переводе узла в состояние Clean.

В оригинальном алгоритме используется прием взаимопомощи (helping) потоков при обнаружении конкуренции на узле. Для этого помимо флагов состояния внутренний узел может содержать дескриптор выполняемой операции — вставки или удаления. Конкурирующий поток, обнаружив состояние узла, отличное от Clean, может прочесть данный дескриптор и попытаться помочь своему собрату выполнить операцию. В этом случае переход в состояние Clean по окончании операции должен производиться только примитивом CAS, так как несколько потоков — инициатор операции и помощники — могут переводить состояние узла в Clean. Если мы будем делать это атомарным store, то возможна ситуация, когда узел, переведенный в состояние Clean и затем в некое другое последующей операцией вставки/удаления, будет переведен опять в Clean неким запоздавшим помощником.

Прием взаимопомощи хорошо выглядит в псевдокоде, но на практике я не видел от него особого выигрыша. Более того, на C++, где нет сборщика мусора, данный прием реализовать эффективно довольно проблематично: сразу встает вопрос о том, как распределять дескрипторы (на стеке? alloc? пул?), а также ещё более серьезный — о времени жизни такого дескриптора (reference counting?). В реализации libcds helping отключен: несколько попыток его внедрения не увенчались успехом, — код получается нестабильным (эта красивая фраза из лексикона менеджеров означает, что программа падает). Так что алгоритм binary search tree в libcds содержит несколько артефактов, в том числе и CAS вместо атомарного store при переводе состояния узла в Clean, от которых в будущем я избавлюсь.

Заключение

В данной статье рассмотрен алгоритм самого простого бинарного дерева. Несмотря на отсутствие балансировки, алгоритм представляет интерес хотя бы потому, что является первым шагом к реализации более сложных, самобалансирующихся деревьев типа AVL-tree и Red-Black tree, работа над которыми ведется, надеюсь скоро представить их в libcds.

Серию статей о concurrent map хотелось бы закончить результатами синтетических тестов для реализаций из libcds (Intel Dual Xeon X5670 2.93 GHz 12 cores 24 threads / 24 GB RAM, среднее число элементов — 1 миллион, ключи — int):

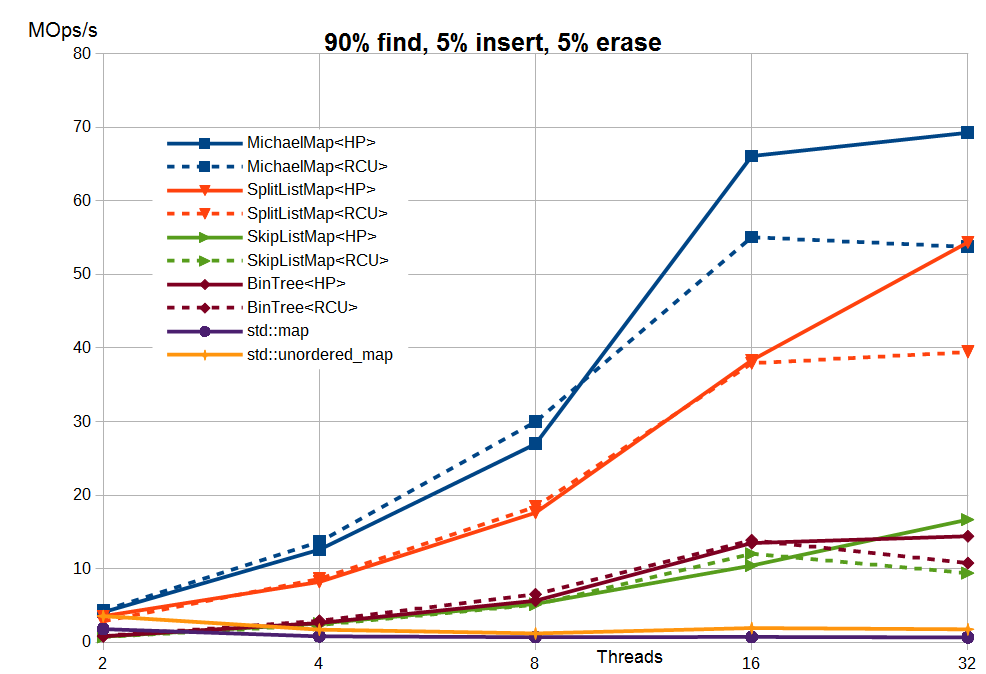
Здесь:

• MichaelMap — простейший hash map без rehasing'а, рассмотренный здесь
• SplitListMap — алгоритм split-ordered list
• SkipListMap — алгоритм skip list
• BinTree — рассмотренное в данной статье бинарное дерево
• std::map, std::unordered_map — STL-алгоритмы под std::mutex

Результаты приведены для Hazard Pointer (HP) и user-space RCU (точнее, её буферизованной разновидности cds::urcu::general_buffered).

Вы можете подтвердить или опровергнуть эти результаты, загрузив и скомпилировав libcds или применив структуры данных из libcds в своем приложении.

Пожалуй, на сегодняшний день это все, что я хотел бы рассказать о lock-free структурах данных. Конец эпического цикла! Есть много вопросов по lock-free и вообще по внутреннему строению контейнеров, которые можно было бы обсудить, но все они весьма технические и, боюсь, не будут интересны широкой публике.

Автор: khizmax

Источник