Пройдем по следам C++ 2015 Russia далее.
В предыдущей статье мы рассмотрели алгоритм для lock-free ordered list и на его основе сделали простейший lock-free hash map. У этого hash map есть недостаток: размер хеш-таблицы постоянен и не может быть изменен в процессе роста числа элементов в контейнере. Это не представляет проблемы, если мы заранее примерно представляем требуемый объем контейнера. А если нет?
Процедура увеличения, равно как и уменьшения, размера хеш-таблицы (rehashing) довольно тяжелая
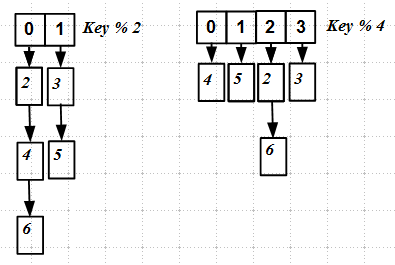
Как видно даже из этой простой картинки, при rehasing'е ключи перераспределяются по другим слотам новой хеш-таблицы, — происходит полная перестройка hash map. Это довольно трудно реализовать атомарно или хотя бы без блокировок.
Многократно мною упоминаемый Nir Shavit совместно с Ori Shalev посмотрел на проблему с другой стороны: хорошо, мы не можем атомарно перераспределить ключи по новым слотам (bucket'ам), но, быть может, мы можем просто вставить новый bucket в уже существующий, таким образом разбивая (splitting) его на две части? Эта идея легла в основу разработанного ими в 2003 году алгоритма split-ordered list.
Split-ordered list
Нельзя просто так взять и вставить новый bucket, – см. рисунок выше: ключи при rehashing'е перераспределяются между bucket'ам, а нам требуется, чтобы их позиции не изменялись. Мы хотим чего-то странного такого:
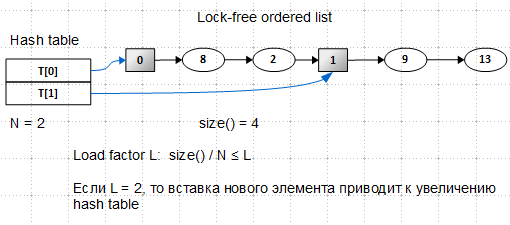
В основе лежит уже рассмотренный нами lock-free ordered list. В нем появилось два типа узлов: регулярные узлы (овальные) и вспомогательные (sentinel) узлы (квадратные). Вспомогательные узлы играют роль меток начала bucket'ов и никогда не удаляются; в хеш-таблице находятся указатели на эти вспомогательные узлы.
Глядя на этот рисунок, вы можете спросить: список упорядоченный, но этого не видно, — ключи расположены хаотично, в чем дело? Ответ: список упорядоченный, но критерий порядка мы изобретем чуть позже.
Итак, мы имеем хеш-таблицу с двумя слотами, указывающими на вспомогательные узлы. Размер списка равен 4 (вспомогательные узлы не учитываются при подсчете количества элементов), load factor равен 2 (это мое волюнтаристское решение). Мы хотим вставить новый элемент с ключом 10:
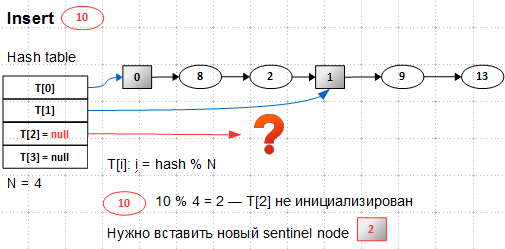
При попытке вставки нового элементы мы выясняем, что наш список переполнен – число элементов становится 5, число bucket'ов равно 2, 5/2 > load factor, — надо расширять таблицу T[]. Предположим, мы каким-то образом её расширили — в ней стало 4 bucket'а, два первых инициализированы, два последних — нет. Новый элемент 10 должен попасть в bucket 2 ( 10 mod 4 = 2, здесь и далее я считаю для наглядности, что hash(key) == key), который ещё не инициализирован. Значит, сначала нужно вставить вспомогательный элемент 2, то есть сделать расщепление какого-то существующего bucket'а. Для начала надо найти этот существующий bucket, называемый родительским (parent):
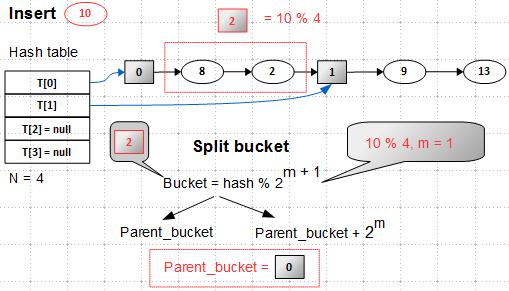
Расщепление bucket'а, пожалуй, самый тонкий момент в алгоритме. Родительский bucket, пока нам не известный, должен находиться в первой половине хеш-таблицы, то есть в нашем случае это bucket 0 или 1.
Bucket – это hash(key) mod 2**(m+1), где 2**(m+1) — размер хеш-таблицы. Новый bucket расщепляет родительский, то есть разделяет элементы родительского bucket'а на два лагеря: одни входят в parent bucket, а вторые — в parent_bucket + 2**m. Отсюда следует, что для нового bucket 2 родительский — это bucket 0.
На C++ процедура вычисления родительского bucket'а выглядит очень просто:
size_t parent_bucket( size_t nBucket )
{
assert( nBucket > 0 );
return nBucket & ~( 1 << MSB( nBucket ) );
}
где MSB – most significant bit – номер старшего единичного бита.
Итак, для вставки элемента 10 прежде всего следует создать новый bucket 2 и вставить его в bucket 0. У нас есть готовый алгоритм упорядоченного списка, так что самое время определиться, как же должен быть упорядочен наш split-ordered list.
Заметим, что все операции, которые мы до сих пор делали, были основаны на арифметике по модулю степени двойки. Посмотрим на бинарное представление ключей:
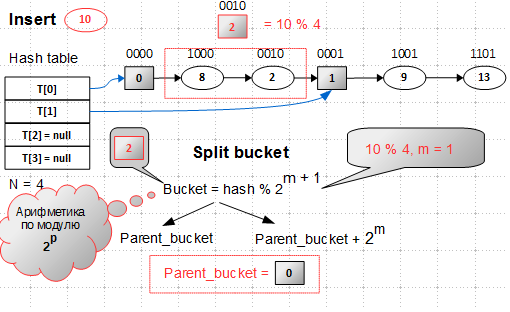
А теперь — внимание: если прочесть бинарные значения ключей справа налево, мы получим отсортированный список:
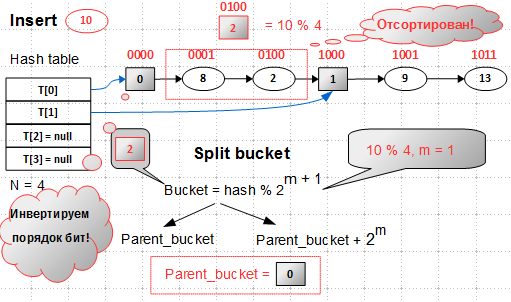
Такие обращенные хеш-значения я называю shah.
Итак, критерий сортировки списка — по обращенным (прочитанным справа налево) хеш-значениям ключей.
uint32_t reverse_bit_order( uint32_t x )
{
// swap odd and even bits
x = ((x >> 1) & 0x55555555) | ((x & 0x55555555) << 1);
// swap consecutive pairs
x = ((x >> 2) & 0x33333333) | ((x & 0x33333333) << 2);
// swap nibbles ...
x = ((x >> 4) & 0x0F0F0F0F) | ((x & 0x0F0F0F0F) << 4);
// swap bytes
x = ((x >> 8) & 0x00FF00FF) | ((x & 0x00FF00FF) << 8);
// swap 2-byte long pairs
return ( x >> 16 ) | ( x << 16 );
}
Последние два действия, обращающие порядок байт, иногда в железе реализованы.
Получается интересно: bucket'ы вычисляются по хеш-значениям ключей, а сортировка — по обращенным хеш-значениям. Главное — не запутаться.
Но и это ещё не все. Взглянув на рисунок ещё раз, мы увидим, что узел с ключом 2 уже есть в списке, — это регулярный узел, а нам надо вставить вспомогательный с тем же самым ключом. Вспомогательные и регулярные узлы — совершенно разные объекты, даже по внутреннему строению: регулярные узлы содержат ключ и значение (value), а вспомогательные, служащие метками начала bucket'ов, — только хеш-значения. Регулярный узел может быть удален из списка, а вот вспомогательный — никогда. Следовательно, нам надо как-то различать эти два типа узлов. Авторы предлагают использовать для этого старший бит хеш-значения (в обращенном хеш-значении это будет младший бит): в хеш-значениях регулярных узлов старший бит выставляется в 1, а во вспомогательных — в 0:
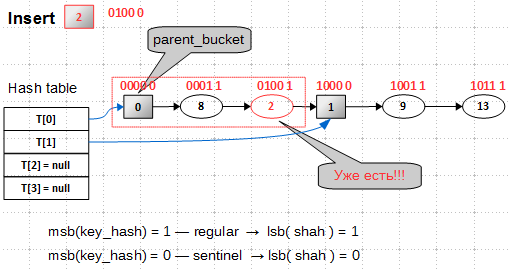
Этот бит также играет роль ограничителя при поиске ключа в bucket'е, — мы никогда не вылезем за границы bucket'а.
Подведем итог всему вышесказанному. Вставка ключа 10 производится в два этапа: сначала добавляется новый вспомогательный узел 2 в родительский bucket 0:
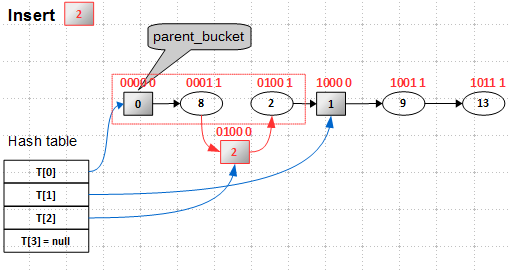
Затем в bucket 2 вставляется элемент с ключом 10:
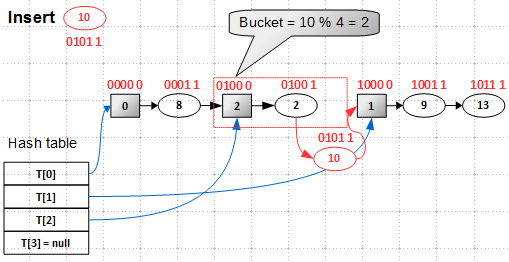
В основе split-ordered list лежит lock-free ordered list, который мы рассматривали в предыдущей статье, так что никаких трудностей со вставкой/удалением быть не должно. Кстати, про удаление, — никаких особенностей алгоритм удаления из split-ordered list не имеет, мы просто вычисляем по ключу bucket и вызываем функцию удаления из lock-free list с началом во вспомогательном узле этого bucket'а. Вспомогательные узлы не удаляются никогда, то есть хеш-таблица в split-ordered list может только динамически расти, но не сжиматься.
Алгоритм split-ordered list интересен тем, что он противоречит всем каноническим представлениям о хеш-таблицах. Вспомним, Кнут в своей монографии доказывает, что для построения хорошей хеш-таблицы её размер должен быть простым числом, следовательно, вся арифметика должна быть по модулю простых чисел. Для split-ordered list все наоборот: этот алгоритм существенно полагается на бинарное представление хеш-значений, вся арифметика ведется по модулю степени двойки. Такая заточенность под 2**N очень хорошо ложится на современные процессоры, которые, несмотря на значительный прогресс, всё ещё тупят на целочисленном делении, а вот замена деления на сдвиги им очень нравится.
Остался один невыясненный вопрос — динамическое расширение хеш-таблицы. Авторы предлагают сегментную организацию хеш-таблицы:
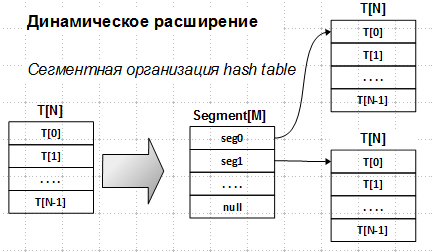
Вместо единого массива T[N] используется массив сегментов Segment[M], создаваемый при инициализации объекта split-ordered list. Здесь M — степень двойки. Номер сегмента — это старшие биты хеш-значения. Каждый сегмент указывает на таблицу T[N], эти таблицы создаются динамически по необходимости, кроме таблицы Segment[0], которая инициализируется при создании объекта split-ordered list (помните, я отмечал, что bucket 0 всегда должен быть).
При такой организации на момент создания объекта-списка все же нужно знать предполагаемое число элементов, чтобы вычислить размер таблицы сегментов M (никакого особого алгоритма этого вычисления нет — мною эмпирически подобраны некие границы, чтобы как Segment[], так и каждая T[] были соизмеримы по размеру). Но все же алгоритм допускает рост хеш-таблицы, пусть и в таком непривычном виде.
Итоги

В этой статье рассмотрен весьма оригинальный алгоритм lock-free split-ordered list, позволяющий делать rehash без rebuild, то есть без перестройки хеш-таблицы. Этот алгоритм также интересен тем, что в своей основе имеет обычный lock-free ordered list и может быть использован как полигон для отладки различных реализаций упорядоченных списков.
Реализация данного алгоритма в libcds показывает очень неплохие результаты в тестах, но все же немного хуже, чем простейший hash map, описанный в предыдущей статье. Этому есть две причины:
- это плата за динамически создаваемые bucket'ы
- обращение порядка бит хеш-значения все-таки довольно тяжелая операция, если она реализована программно. Интересно было бы иметь данную операцию в железе
С архитектурной точки зрения, очень увлекательно было этот алгоритм разрабатывать, чтобы выделить ordered list как стратегию для split-ordered list.
В следующей статье я расскажу об ещё одной реинкарнации lock-free ordered list. На сей раз будем строить не hash map, а упорядоченный map.
Автор: khizmax






