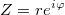Квантовая песочница: часть 2

Квантовая песочница: часть 1
Что такое квантовое состояние? Чем обычное состояние отличается от квантового? В какой момент обычное состояние становится квантовым и что будет, если от него отнять квантовости? Оно всё еще будет квантовым или уже превратится в обычное? Оно же только что было квантовым. Наверное, оно стало запутанным, и кот тоже стал запутанным.

В данной статье постараемся ответить на эти вопросы и разобраться в сути квантовой механики.
Цель: написать простую программу, «имитирующую» квантовую эволюцию, чтобы наконец можно было пощупать эти кубиты ручками.

Оглавление:

• Часть I: Классическое состояние
• Часть II: Квантовое состояние
• Часть III: Кот
• Часть IV: Рой

Что такое обычное «состояние»? Этим термином пользуются так часто, что он начал восприниматься полностью интуитивно.

Вопрос №1: «Дана частица P, которую можно наблюдать вдоль отрезка . Что такое состояние частицы P?»
Ответ: Классическое состояние частицы P — число из отрезка .

Внимательного читателя привлечет слово «наблюдать» — как это вообще понимать?
Оказалось, что все это время на участке 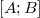были расположены какие-то «детекторы», которые «наблюдали», но почему мы о них ничего не сказали? И сколько их там вообще штук?

Мы сказали, что состояние частицы — число из отрезка 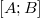. Мощность множества 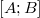равна континууму — между нашими «границами» А и B находится бесконечно много чисел, причем они расположены бесконечно близко друг к другу — значит нам требуется бесконечно много детекторов для каждой точки? Звучит довольно затратно, не так ли?

А ведь, утверждая, что состояние есть число, мы, получается, подразумеваем именно это. Именно то, что у нас в наличии бесконечно много детекторов. Но ведь это не так. И такого не может быть в принципе.

На практике мы бы разбили отрезок на конечное число сегментов, а в пересечениях поставили бы детекторы, и каждый детектор был бы способен приближенно сообщить, есть ли частица в его окрестности или нет.

То, что было сделано выше называется квантованием. В данном случае мы провели квантование отрезка на сегменты. Квант — неделимая порция чего-либо в рамках используемой модели, абстрактный термин.

Самые интересные явления начинаются именно по той причине, что состояние частицы теперь перестало быть просто числом.

Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности некоторого числа детекторов на отрезке . Что такое состояние частицы P?»
Ответ: ???

Рассмотрим пример:

Дан отрезок 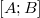и два детектора, расположенные в точках A и B.

Каждый детектор показывает какое-то определенное число, согласно которому мы можем определить, как далеко находится частица от данного детектора.

A — первый детектор, 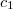— его показания ( 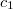= 1, если частица попала прямо в А)
B — второй детектор, 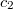— его показания ( 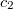= 1, если частица попала прямо в В)

Выдвинем предположение о частице, чтобы как-то ограничить круг наших исследований:

Предположение: Частица одна, она не может просто так взять и клонировать себя.

Из этого предположения следует, что если частица в А, то она не может быть в В, и наоборот.

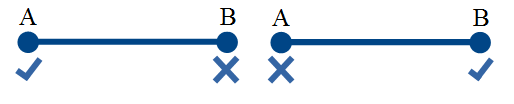
Или, что то же самое, если 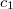= 1, то 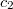= 0 и наоборот.

Теперь рассмотрим «движение» частицы от детектора А к детектору В. Частица была в А (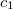 = 1, 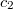= 0), затем она начала лететь к В. Показания детектора А начали уменьшаться ( 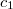< 1), а показания детектора В начали увеличиваться ( 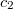> 0). Затем частица достигла детектора В и его показания равны 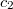= 1, а детектор А оповещает нас, что частицы в нем нет 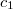= 0.

Таким образом, мы описываем состояние частицы с помощью самих детекторов и их показаний.

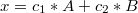
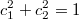
Это запись означает, что конфигурация X включает в себя детектор A, показывающий нам число c1, и детектор B, показывающий нам число c2.

Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности детекторов, расположенных в точках A и B, которые являются квантованием отрезка на один сегмент . Что такое состояние частицы P?»
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Ответ: Квантовое состояние частицы P — вектор двумерного гильбертова пространства с базисными векторами A = {1, 0} и B = {0, 1}. При этом этот вектор нормирован на единицу (), а базисные векторы A и B являются классическими состояниями из вопроса 1. Такие частицы также называют кубитами в силу двумерности базиса. Когда базис трехмерный, частицы называются кутритами и т. д.

Вопрос №2 (обобщенный): «Дана частица P, которую можно наблюдать только в окрестности конечного числа детекторов, расположенных в точках , которые являются квантованием отрезка на N — 1 сегмент . Что такое состояние частицы P?»
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Ответ: Квантовое состояние частицы P — вектор N-мерного гильбертова пространства с базисными векторами . При этом этот вектор нормирован на единицу , а базисные векторы являются классическими состояниями из вопроса 1.

Мы вплотную подошли к самым интересным проявлениям квантовой механики. Без сомнения каждый из читателей хоть краем уха слышал о таких терминах, как «квантовая суперпозиция» или «квантовая запутанность» — эти эффекты и другая подобная магия начинаются именно в тот момент, когда вы не будете делать тех умозаключений, которые не требуются.

У нас есть два определения состояния.

Определение №1: Классическое состояние частицы P — число из отрезка …
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Определение №2: Квантовое состояние частицы P — вектор двумерного гильбертова пространства …

Обычно из каких-то определений выводят следствия, здесь же нас будет интересовать то, что не следует из определения, но мы все равно назовем это следствиями для стройности.

Следствие №1: Из определения квантового состояния не следует, что частица находится в одной точке отрезка. Вообще ниоткуда никак не следует.

То есть частица может находится сразу в двух точках! Например для частицы, которая находится в квантовом состоянии 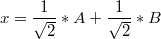не следует, что она находится в одной точке. Да, может быть она где-то посередине, в какой-то точке M между A и B, но утверждая подобное, мы проявим необоснованную вольность.

Следствие №2: Из определения квантового состояния не следует, что частица разделилась на маленькие кусочки, одни кусочку полетели туда, а другие сюда.

Как это вообще понимать? Как частица может находится сразу в двух точках и при этом оставаться неделимой? Мы же привыкли, что кот Шрёдингера и жив, и мертв одновременно, значит и частица тоже и здесь, и там одновременно. Но ведь она же неделима. Она что растянулась?

Введем понятие роя и экземпляра виртуальных частиц.

Определение №3: Экземпляр частицы — виртуальный объект, которому соответствует положение в пространстве в данный момент времени, траектория движения с течением времени, а также комплексное число (называемое амплитудой), обладающее модулем и аргументом, для которого справедливы все алгебраические правила:
Определение №4: Рой — совокупность экземпляров.
Определение №5: Частица — рой (при выполнении операции квантования пространства).

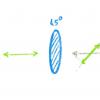
Представим экземпляр как шарик, внутри которого есть стрелка, соответствующая комплексному числу в комплексной плоскости. Важно понимать, что шарик может иметь одно направление движения, а стрелка внутри него — другое, то есть эти направления разные.

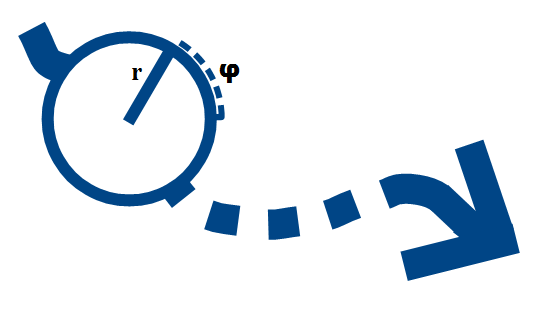
Но почему разные? Дело в том, что процессы внутри элементарной частицы настолько сложно описать, что влияние этих процессов на движение самой частицы невозможно предсказать на фундаментальном уровне, поэтому и связи между стрелкой внутри шарика и направлением движения самого шарика для нас не существует.

Словесные манипуляция, которые мы сейчас совершили, бесполезны, если не определить законы изменения величин r, φ и закон движения, ведь в них все и упирается.

Закон изменения аргумента: φ постоянно равномерно увеличивается на величину dφ по мере движения экземпляра.

Иными словами, наши комплексное стрелки постоянно крутятся в одном и том же направлении. Зачем это нужно? Чтобы система ни при каких обстоятельствах не перестала эволюционировать.

Закон сложения и умножения: По мере движения вдоль одного пути амплитуды перемножаются. Амплитуды вдоль всевозможных путей складываются.

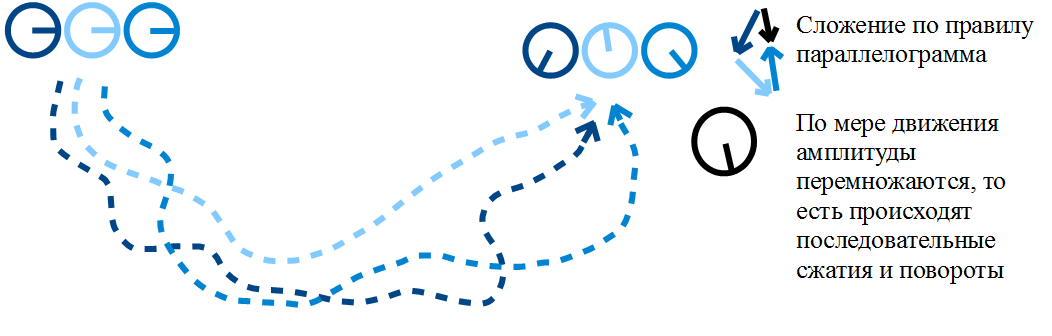
Данный закон также известен как «принцип суперпозиции в квантовой механике»

Закон движения экземпляров в пространстве: Пусть дана частица в квантовом состоянии. Дан экземпляр, которые находится в какой-то клетке пространства (над которым была произведена операция квантования на клетки). Вокруг этой клетки пространства есть соседние клетки.

1. Данный экземпляр клонирует себя столько раз, сколько вокруг него существует соседних точек
2. Каждый клон движется в ту соседнюю точку, которая ему соответствует
3. Данный экземпляр-отец движется в произвольную точку

Процесс повторяется для каждого экземпляра.

Мы не забываем, что внутри каждого шарика находится комплексная стрелка, которая имеет свое направление и длину. Как предсказать, какая результирующая стрелка окажется в произвольной клетке пространства в данный момент времени? Очевидно, для этого нужно знать, что было со всей системой в предыдущий момент времени. Мы получаем дифференциальное уравнение (его называют уравнением Шрёдингера в честь Шрёдингера, который его и открыл).

Закон движения экземпляров в пространстве: Пусть — квантовое состояние частицы, вектор-столбец, в котором одна за другой записаны амплитуды во всех клетках пространства. — оператор энергии, определяющий способ взаимодействия между экземплярами. Тогда рой движется согласно следующему закону: .

Формирование оператора энергии «по кусочкам ручками» будет рассмотрено в следующей статье.

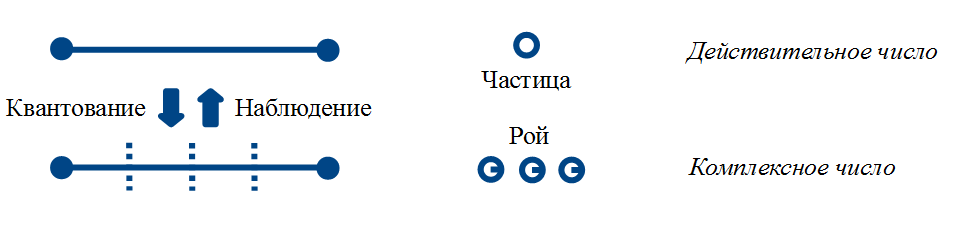
Конструктивно, мы разобрались со следующими понятиями:

1. Классическое состояние частицы как число (а не как что-либо еще)
2. Квантовое состояние частицы как вектор (а не как «то, что находится сразу в нескольких местах»)
3. Частица как рой (при выполнении операции квантования)
4. Принцип суперпозиции роя, согласно которому амплитуды вдоль одного пути перемножаются, а вдоль всевозможных путей складываются
5. Закон движения экземпляров

В следующей статье мы рассмотрим самое интересное — системы с произвольным количеством частиц. Разберем, что же такое тензоры, запутанные состояния и, наконец, напишем программу, способную «имитировать» квантовую эволюцию и удобно её отрисовывать.

Поскольку тема квантовой механики активно популяризируется в последнее время (начиная от соответствующих журналов, заканчивая целыми выставками, посвященными «квантовой запутанности»), мне кажется, что есть потребность в мониторинге актуального состояния, чтобы можно было зайти и проверить «а что там у нас с квантами?» Возможно, эта информация будет полезной — pleaded.ru

Автор: pleaded

Источник