Содержание основного курса
- Статья 1: алгоритм Брезенхэма
- Статья 2: растеризация треугольника + отсечение задних граней
- Статья 3: Удаление невидимых поверхностей: z-буфер
- Статья 4: Необходимая геометрия: фестиваль матриц
- Статья 5: Пишем шейдеры под нашу библиотеку
- Статья 6: Чуть больше, чем просто шейдер: просчёт теней
Улучшение кода
- Статья 3.1: Настала пора рефакторинга
- красивый класс матриц
- как работает новый растеризатор
Пришла пора веселья, давайте для начала смотреть размер текущего кода:
- geometry.cpp+.h — 218 строк
- model.cpp+.h — 139 строк
- our_gl.cpp+.h — 102 строки
- main.cpp — 66 строк
Итого 525 строк. Ровно то, что я обещал в самом начале курса. И заметьте, что отрисовкой мы занимаемся только в our_gl и main, а это всего 168 строк, и нигде мы не вызывали сторонних библиотек, вся отрисовка сделана нами с нуля!
Я напоминаю, что мой код нужен только для финального сравнения с вашим работающим кодом! По-хорошему, вы всё должны написать с нуля, если следуете этому циклу статей. Очень прошу, делайте самые безумные шейдеры и выкладывайте в комментарии картинки!!!

Чёрные треугольники на рогах — это модель битая слегка, просто мне надоела голова старого негра, а чинить не сильно хочется.
Рефакторим наш код, чтобы он походил на структуру OpenGL
Итак, наш main.cpp начинает слегка разрастаться, поэтому давайте его разделим на две части
- our_gl.cpp + .h — это часть, которую мы программировать не можем, грубо говоря, бинарный файл библиотеки.
- main.cpp — здесь мы можем программировать что хотим.
Давайте подробнее, что я вынес в our_gl? Фунции построения матриц проекции, вида и перехода к экранным координатам, а также сами матрицы просто глобальными переменными. Ну и функцию-растеризатор треугольника. Всё!
Вот содержимое файла our_gl.h (про назначение IShader чуть позже):
#include "tgaimage.h"
#include "geometry.h"
extern Matrix ModelView;
extern Matrix Viewport;
extern Matrix Projection;
void viewport(int x, int y, int w, int h);
void projection(float coeff=0.f); // coeff = -1/c
void lookat(Vec3f eye, Vec3f center, Vec3f up);
struct IShader {
virtual ~IShader() = 0;
virtual Vec3i vertex(int iface, int nthvert) = 0;
virtual bool fragment(Vec3f bar, TGAColor &color) = 0;
};
void triangle(Vec3i *pts, IShader &shader, TGAImage &image, TGAImage &zbuffer);
В файле main.cpp осталось всего 66 строк, поэтому я его даю целиком (извините за простыню, но мне этот файл настолько нравится, что я не буду его прятать под спойлер):
#include <vector>
#include <iostream>
#include "tgaimage.h"
#include "model.h"
#include "geometry.h"
#include "our_gl.h"
Model *model = NULL;
const int width = 800;
const int height = 800;
Vec3f light_dir(1,1,1);
Vec3f eye(1,1,3);
Vec3f center(0,0,0);
Vec3f up(0,1,0);
struct GouraudShader : public IShader {
Vec3f varying_intensity; // written by vertex shader, read by fragment shader
virtual Vec3i vertex(int iface, int nthvert) {
Vec4f gl_Vertex = embed<4>(model->vert(iface, nthvert)); // read the vertex from .obj file
gl_Vertex = Viewport*Projection*ModelView*gl_Vertex; // transform it to screen coordinates
varying_intensity[nthvert] = std::max(0.f, model->normal(iface, nthvert)*light_dir); // get diffuse lighting intensity
return proj<3>(gl_Vertex/gl_Vertex[3]); // project homogenious coordinates to 3d
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
float intensity = varying_intensity*bar; // interpolate intensity for the current pixel
color = TGAColor(255, 255, 255)*intensity; // well duh
return false; // no, we do not discard this pixel
}
};
int main(int argc, char** argv) {
if (2==argc) {
model = new Model(argv[1]);
} else {
model = new Model("obj/african_head.obj");
}
lookat(eye, center, up);
viewport(width/8, height/8, width*3/4, height*3/4);
projection(-1.f/(eye-center).norm());
light_dir.normalize();
TGAImage image (width, height, TGAImage::RGB);
TGAImage zbuffer(width, height, TGAImage::GRAYSCALE);
GouraudShader shader;
for (int i=0; i<model->nfaces(); i++) {
Vec3i screen_coords[3];
for (int j=0; j<3; j++) {
screen_coords[j] = shader.vertex(i, j);
}
triangle(screen_coords, shader, image, zbuffer);
}
image. flip_vertically(); // to place the origin in the bottom left corner of the image
zbuffer.flip_vertically();
image. write_tga_file("output.tga");
zbuffer.write_tga_file("zbuffer.tga");
delete model;
return 0;
}
Давайте его разберём детально. Заголовки пропускаем, затем идут глобальные константы: размеры экрана, где находится камера и т.п.
Структуру GouraudShader разберём в следующем абзаце, пропускаем. Затем идёт непосредственно main():
- Чтение модели из .obj файла
- Инициализация матриц ModelView, Projection и Viewport (напоминаю, сами переменные хранятся в модуле our_gl)
- Проход по модели и её отрисовка
В последнем пункте начинается самое интересное. Внешний цикл проходит по всем треугольникам.
Внутренний цикл проходит по всем вершинам треугольника и для каждой из них вызывает вершинный шейдер.
Главное назначение вершинного шейдера — посчитать преобразованные координаты вершин. Второстепенное — подготовить данные для работы фрагментного шейдера.
Что происходит после того, как мы вызвали вершинный шейдер для всех вершин в треугольнике? Мы можем вызвать растеризатор нашего треугольника. Что происходит внутри него мы не знаем (не, ну, мы его сами написали, конечно). Кроме одной интересной вещи. Растеризатор треугольника вызывает нашу функцию, которую мы ему даём — фрагментный шейдер. То есть, ещё раз, для каждого пикселя внутри треугольника растеризатор вызывает фрагментный шейдер.
Главное назначение фрагментного шейдера — это определить цвет текущего пикселя. Второстепенное — мы можем вообще отказаться рисовать этот пиксель, вернув true.
Пайплайн OpenGL 2 выглядит так:
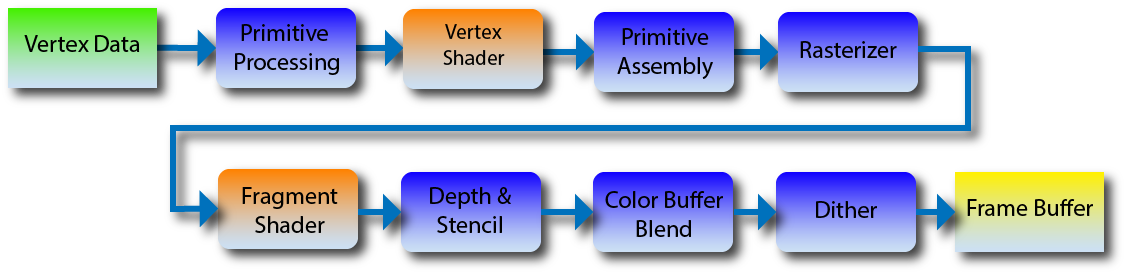
Поскольку у нас краткий курс графики, пока ограничимся этими двумя шейдерами. В более новых версиях OpenGL появились новые виды шейдеров, которые позволяют создавать геометрию на лету. На этой картинке синим показаны этапы, которые мы программировать не можем, а рыжим те, что можем. По факту, наша main() — это primitive processing. Она вызывает вершинный шейдер. Сборщика примитивов у нас нет, т.к. мы рисуем тупые треугольники напрямую (он у нас склеился с primitive processing). Функция triangle() — это растеризатор, для каждой точки она вызывает фрагментный шейдер и затем делает проверки глубины в z-буфере и так далее.
Всё. Вы знаете, что такое шейдеры, и можете приступать к их программированию.
Как работает моё воплощение шейдеров на примере тонировки Гуро
Давайте разберём те шейдеры, что я привёл в коде main.cpp. Как нетрудно догадаться, первый шейдер — это тонировка Гуро.

Вершинный шейдер читает вершину из .obj файла, погружает её в четырёхмерное пространство (см. предыдущую статью), находит её экранные координаты. Возвращает спроецированную в 3д точку, но перед этим считает коэффициент диффузной освещённости для данной вершины и сохраняет его в соответствующую компоненту вектора varying_intensity.
Ещё раз код для удобства:
Vec3f varying_intensity; // written by vertex shader, read by fragment shader
virtual Vec3i vertex(int iface, int nthvert) {
Vec4f gl_Vertex = embed<4>(model->vert(iface, nthvert)); // read the vertex from .obj file
gl_Vertex = Viewport*Projection*ModelView*gl_Vertex; // transform it to screen coordinates
varying_intensity[nthvert] = std::max(0.f, model->normal(iface, nthvert)*light_dir); // get diffuse lighting intensity
return proj<3>(gl_Vertex/gl_Vertex[3]); // project homogenious coordinates to 3d
}
varying — это зарезервированное слово в языке GLSL, я использовал varying_intensity в качестве имени просто чтобы подчеркнуть параллель между ними (о GLSL мы поговорим в седьмой статье). Мы сохраняем в структуре varying данные, которые будут интерполированы внутри треугольника, и фрагментный шейдер получит уже интерполированные данные.
Разберём фрагментный шейдер, ещё раз код для удобства:
Vec3f varying_intensity; // written by vertex shader, read by fragment shader
// [...]
virtual bool fragment(Vec3f bar, TGAColor &color) {
float intensity = varying_intensity*bar; // interpolate intensity for the current pixel
color = TGAColor(255, 255, 255)*intensity; // well duh
return false; // no, we do not discard this pixel
}
Он вызывается растеризатором для каждого пикселя внутри треугольника. Он получает на вход барицентрические координаты для интерполирования данных varying_.
То есть, интерполированная интенсивность может быть посчитана как varying_intensity[0]*bar[0]+varying_intensity[1]*bar[1]+varying_intensity[2]*bar[2] или просто-напросто скалярным произведением между векторами varying_intensity*bar. В настоящем GLSL, конечно, шейдер получает уже готовое значение.
Обратите внимание, что фрагментный шейдер возвращает булевское значение. Его значение легко понять, если посмотреть внуть растеризатора (our_gl.cpp, triangle()):
TGAColor color;
bool discard = shader.fragment(c, color);
if (!discard) {
zbuffer.set(P.x, P.y, TGAColor(P.z));
image.set(P.x, P.y, color);
}
Шейдер может отказаться рисовать данный пиксель, тогда растеризатор игнорирует и его z-координату, не обновляя z-буфер. Полезно если мы хотим делать бинарные маски или что ещё вам в голову придёт.
Разумеется, растеризатору и в голову не может прийти то, что придёт в голову вам, поэтому он компилироваться с вашим шейдером заранее не может. Тут нам приходит на помощь абстрактный класс IShader. Уфф, нечасто я пользуюсь абстрактными классами, но тут ровно случай, когда без него было бы плохо. Передавать указатели на функции мне не хочется совсем!
Первая модификация
virtual bool fragment(Vec3f bar, TGAColor &color) {
float intensity = varying_intensity*bar;
if (intensity>.85) intensity = 1;
else if (intensity>.60) intensity = .80;
else if (intensity>.45) intensity = .60;
else if (intensity>.30) intensity = .45;
else if (intensity>.15) intensity = .30;
else intensity = 0;
color = TGAColor(255, 155, 0)*intensity;
return false;
}
Просто я разрешаю некий фиксированный набор интенсивностей освещения. Вот результат его работы:

Текстурируем модель
Тонировку Фонга пропускаем, её подробно разобрали в комментариях, давайте наложим текстуры. Для этого придётся интерполировать uv-координаты. Ничего нового, просто добавляем матрицу в две строки (uv) и три столбца (текстурные координаты трё вершин).
struct Shader : public IShader {
Vec3f varying_intensity; // written by vertex shader, read by fragment shader
mat<2,3,float> varying_uv; // same sa above
virtual Vec3i vertex(int iface, int nthvert) {
varying_uv.set_col(nthvert, model->uv(iface, nthvert));
varying_intensity[nthvert] = std::max(0.f, model->normal(iface, nthvert)*light_dir); // get diffuse lighting intensity
Vec4f gl_Vertex = embed<4>(model->vert(iface, nthvert)); // read the vertex from .obj file
gl_Vertex = Viewport*Projection*ModelView*gl_Vertex; // transform it to screen coordinates
return proj<3>(gl_Vertex/gl_Vertex[3]); // project homogenious coordinates to 3d
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
float intensity = varying_intensity*bar; // interpolate intensity for the current pixel
Vec2i uv = varying_uv*bar; // interpolate uv for the current pixel
color = model->diffuse(uv)*intensity; // well duh
return false; // no, we do not discard this pixel
}
};

Normalmapping
Окей, теперь у нас есть текстурные координаты. Но ведь в текстурах можно хранить не только цвет, RGB вполне хватает для представления xyz!
Давайте загрузим вот такую текстуру, которая для каждого пикселя нашей картинки (а не только для вершин, как раньше!) даст вектор нормали.

Кстати, сравните его с такой картинкой, это та же самая информация, но в другом репере:

Одна из этих картинок даёт нормальные векторы в глобальной системе координат, а другая в касательной, которая определяется для каждой точки нашего объекта. В этой текстуре вектор z — это нормаль к объекту, вектор x — это вектор главного направления кривизны поверхности, а y — это их векторное произведение.
Упражнение 1
Скажите, какая из этих текстур дана в глобальных координатах, а какая в касательных к объекту?
Упражнение 2
Какой формат текстуры предпочтительнее — касательный или глобальный? Почему?
Пожалуйста, не стесняйтесь (не читая комментариев заранее) дать ответы на эти вопросы в комментариях!
struct Shader : public IShader {
mat<2,3,float> varying_uv; // same sa above
mat<4,4,float> uniform_M; // Projection*ModelView
mat<4,4,float> uniform_MIT; // (Projection*ModelView).invert_transpose()
virtual Vec3i vertex(int iface, int nthvert) {
varying_uv.set_col(nthvert, model->uv(iface, nthvert));
Vec4f gl_Vertex = embed<4>(model->vert(iface, nthvert)); // read the vertex from .obj file
gl_Vertex = Viewport*Projection*ModelView*gl_Vertex; // transform it to screen coordinates
return proj<3>(gl_Vertex/gl_Vertex[3]); // project homogenious coordinates to 3d
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
Vec2i uv = varying_uv*bar; // interpolate uv for the current pixel
Vec3f n = proj<3>(uniform_MIT*embed<4>(model->normal(uv))).normalize();
Vec3f l = proj<3>(uniform_M *embed<4>(light_dir )).normalize();
float intensity = std::max(0.f, n*l);
color = model->diffuse(uv)*intensity; // well duh
return false; // no, we do not discard this pixel
}
};
[...]
Shader shader;
shader.uniform_M = Projection*ModelView;
shader.uniform_MIT = (Projection*ModelView).invert_transpose();
for (int i=0; i<model->nfaces(); i++) {
Vec3i screen_coords[3];
for (int j=0; j<3; j++) {
screen_coords[j] = shader.vertex(i, j);
}
triangle(screen_coords, shader, image, zbuffer);
}
Ключевое слово uniform в GLSL позволяет передавать в шейдеры константы, здесь я в шейдер передал матрицу Projection*Modelview и её обратную транспонированную для того, чтобы преобразовать нормальные векторы (см. предыдущую статью).
То есть, всё то же, что и раньше, только вектор нормали мы не интерполируем, а берём из заготовленной текстуры, не забыв при этом вектор направления света и вектор нормали преобразовать надлежащим образом.

Блестящие поверхности или specular mapping
Продолжаем разговор! Для (дешёвого) обмана глаза мы используем приближение Фонга для освещения модели. Итоговая засвеченность данного участка составляется из постоянного освещения для всей сцены (ambient lighting), освещённости для матовых поверхностей, которые мы считали до сих пор (diffuse lighting) и освещённости для глянцевых поверхностей (specular lighting):

Засвеченность матовых поверхностей мы считали как косинус угла между вектором нормали и вектором света. То есть, мы предполагали, что поверхность рассеивает свет примерно во всех направлениях. Что происходит для глянцевых поверхностей? В предельном случе (для зеркальных поверхностей) мы имеем засвет если из этого пикселя видим источник света.
Вот картинка:

Если для данной точки освещённость для матовых поверхностей мы считали как косинус угла между векторами n и l, то теперь нам интересен косинус угла между векторами r (отражённый свет) и v (направление взгляда).
Упражнение 3: найдите вектор r, имея векторы n и l
Напоминаю, что мы засвет для матовой поверхности считали как косинус угла. Но ведь глянцевая отражает источник в гораздо более сфокусированный пучок! Что будет, если мы сделаем то же самое, только этот косинус возведём в десятую степень? Напоминаю, что числа меньше единицы в десятой степени уменьшатся относительно себя же! То есть, десятая степень даст существенно меньший радиус засвета. А сотая ещё меньший. Эта степень хранится в текстуре, которая даёт глянцевость для каждой точки поверхности.
struct Shader : public IShader {
mat<2,3,float> varying_uv; // same sa above
mat<4,4,float> uniform_M; // Projection*ModelView
mat<4,4,float> uniform_MIT; // (Projection*ModelView).invert_transpose()
virtual Vec3i vertex(int iface, int nthvert) {
varying_uv.set_col(nthvert, model->uv(iface, nthvert));
Vec4f gl_Vertex = embed<4>(model->vert(iface, nthvert)); // read the vertex from .obj file
gl_Vertex = Viewport*Projection*ModelView*gl_Vertex; // transform it to screen coordinates
return proj<3>(gl_Vertex/gl_Vertex[3]); // project homogenious coordinates to 3d
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
Vec2i uv = varying_uv*bar;
Vec3f n = proj<3>(uniform_MIT*embed<4>(model->normal(uv))).normalize();
Vec3f l = proj<3>(uniform_M *embed<4>(light_dir )).normalize();
Vec3f r = (n*(n*l*2.f) - l).normalize(); // reflected light
float spec = pow(std::max(r.z, 0.0f), model->specular(uv));
float diff = std::max(0.f, n*l);
TGAColor c = model->diffuse(uv);
color = c;
for (int i=0; i<3; i++) color[i] = std::min<float>(5 + c[i]*(diff + .6*spec), 255);
return false;
}
};
Собственно, тут и объяснять нечего, кроме как коэффициентов. В строчке
for (int i=0; i<3; i++) color[i] = std::min<float>(5 + c[i]*(diff + .6*spec), 255);
Я взял 5 для ambient, 1 для diffuse и .6 для specular. Какие именно брать — вам решать. Это даёт впечатление разных материалов. Чаще всего они даны артистом, но в данном случае у меня их нет, поэтому я взял примерно от балды.

Заключение
Мы научились рендерить весьма правдобоподбные сцены, но освещение ещё далеко от идеала. В следующей статье я расскажу о том, что такое shadow mapping. В одной из ортогональных статей я расскажу о том, как работает новый растеризатор (ничто не мешает запустить этот же код на старом растеризаторе!).
Автор: haqreu






