Эту лампу мне подарили на день рождения в прошлом году. Замечательная маленькая вещица — вы можете перемещать отдельные фрагменты, создавая любую форму, а они светятся по отдельности, питаясь через проводящие грани по периметру.
Из-за очевидной связи с тетрисом меня всегда раздражала одна вещь: лампу невозможно составить в чистый прямоугольник. Как бы я ни старался, всегда какой-нибудь кусочек торчал сбоку, а одного не хватало сверху, или получалась другая раздражающая комбинация.

Это раздражение распространялось на многих, кто посещал мою комнату. В частности, один товарищ потратил целый вечер, перебирая фрагменты в разных комбинациях и отказываясь признать, что у кого-то настолько извращённый ум и он успешно спроектировал фрагменты, которые невозможно составить вместе.
Его усилия оказались тщетными. С тех пор я смирился, что лампу, вероятно, невозможно составить в прямоугольник из-за специально подобранного набора фрагментов.
Однако, выпивая прошлым вечером в комнате, другой мой друг (который раньше не подвергался аморальному влиянию лампы) увидел конструкцию на столе, подумал несколько минут и придумал доказательство, что её действительно нельзя составить в прямоугольник. Доказательство оказалось настолько простым и элегантным, что я решил опубликовать его здесь.

Сама лампа состоит из семи отдельных частей: суммарно, это 28 квадратных фрагментов. Таким образом, если мы хотим сформировать правильную фигуру, она должна иметь размеры 7х4 или 14х2. Здесь мы показываем первый вариант просто потому, что у него более естественная форма. Но доказательство действует и для второй фигуры. Теперь представим, что мы пометили каждый квадрат цветом — чёрным или белым — так что вместе они формируют поверхность вроде шахматной доски, как показано вверху. Заметьте, что количество чёрных клеток должно быть равно количеству белых. Именно этим свойством мы будем оперировать.
Итак, получается 14 чёрных клеток и 14 белых. Если посмотреть отдельно на каждый блок, то проблема сразу становится очевидной.
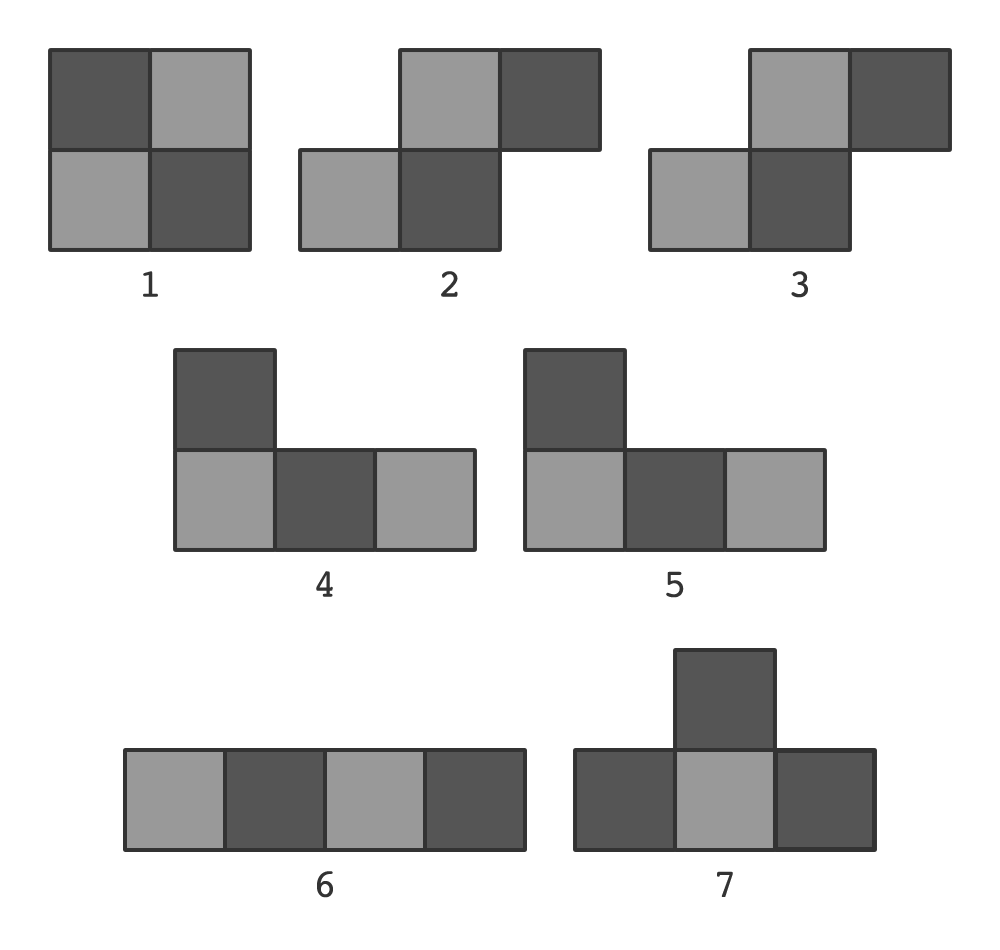
Как видим, для блоков 1-6 количество чёрных фрагментов равно количеству белых. Естественно, местоположение белых и чёрных фрагментов зависит от позиции блока в прямоугольнике, но сама форма указывает количество таких фрагментов (поскольку соседние фрагменты должны быть разных цветов).
Однако, блок 7 нарушает гармонию. Независимо от того, как его разместить, он всё равно состоит из трёх фрагментов одного цвета и одного фрагмента другого цвета, это свойство напрямую следует из его формы.
Таким образом, если посчитать расцветку на всех блоках, то получится 13 клеток одного цвета и 15 клеток другого цвета, независимо от расположения блоков в общей структуре. А ведь нам нужно по 14 фрагментов каждого цвета, но мы никак не можем их получить, так что изначальное условие невозможно соблюсти, что и требовалось доказать.


Вывод
Доказательство само по себе настолько простое: я даже разочарован, что сам не нашёл его раньше. Тем не менее, приятно знать, что не придётся больше тратить время на бездумное тасование фрагментов в надежде на прорыв.
Может быть, мне стоит перенести свой раздражение с самой лампы на того, кто умышленно спроектировал её таким образом.
Автор: alizar





