Всем известно еще со школы как выглядит график гиперболы, не правда ли? Для тех кто подзабыл, напоминаю, что уравнение вида y = k/x — и есть гипербола. Однако это частный случай так называемой равнобокой гиперболы. Для получения более точного представления, определение звучит так: гипербола— геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно. Ну да вернемся к более простому и понятному, к чему нас всех учили – равнобокой гиперболе. Рассмотри классический график ее построения:y = k/x, где ( k > 0 ) и ветви располагаются в I и III четвертях системы координат Рис 1. Гипербола.
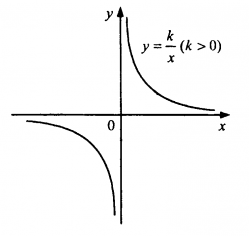
Рис 1. Гипербола
Как видим ветви бесконечно приближаются и стремятся пересечь оси координат. Как можно это охарактеризовать? То есть, если допустим, что ветви гиперболы должны пересечь оси координат в точке y = +-5, x= +-5, а сейчас мы движемся в точке y = +-4, x= +-4, то следующая точка координат будет y = +-4,1, x= +-4,1, и так далее до y = +-4,991, x= +-4,991. Становится понятно, что бесконечность будет расти, и точка с координатами +-4,991, постоянно будут прибавлять в знаке после запятой, что влечет за собой недосягаемость пересекаемой точки на координатных прямых. Все бы хорошо, но посмотрим на это с другой стороны. Допустим мы начинаем строить гиперболу в точке y = +-1, x= +-1. Следуя закону бесконечности, мы никогда не дойдем до точки +-2. Координаты +-1,001, будут постоянной прибавлять в одном знаке после целого числа. То есть до координат +-1,1 или более того до +-1,01, мы не сможем добраться. А если еще глубже посмотреть то точку с координатами y = +-1, x= +-1. или любую другую, мы также не сможем найти на координатной прямой. Это связано с тем, что если взять координаты y = 0, x= 0, и начать движение то получим следующее: (0*10^бесконечность) будет постоянно расти и увидеть 1, в сколько угодно большой степени, после целого нуля невозможно.
На базе рассмотренного можно сделать вывод, что если углубиться в понимания бесконечности на примере гиперболы видно, что в общем построить график невозможно, или даже поставить точку с требуемыми координатами, а в школе мы это все делали элементарно на бумаге в клеточку!
Кто знает, может бесконечность не такая уж и бесконечность, и также как школьная тетрадь, где-то там ограничена красными полями?






