Вопрос эффективного способа реализации очереди с приоритетом некоторой структурой данных остается актуальным в течении долгого времени. Ответ на данный вопрос всегда является неким компромиссом между объёмом памяти, необходимым для хранения данных и временем работой операций над очередью.
В компьютерных науках для эффективной реализации очереди с приоритетом используются структуры в виде кучи.
Куча — это специализированная структура данных типа дерево, которая удовлетворяет свойству кучи: если B является узлом-потомком узла A, то ключ(A) ≥ ключ(B). Из этого следует, что элемент с наибольшим ключом всегда является корневым узлом кучи, поэтому иногда такие кучи называют max-кучами (в качестве альтернативы, если сравнение перевернуть, то наименьший элемент будет всегда корневым узлом, такие кучи называют min-кучами). Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи, хотя на практике их число обычно не более двух. Кучи имеют решающее значение в некоторых эффективных алгоритмах на графах, таких как алгоритм Дейкстры и сортировка методом пирамиды.
Одними из наиболее изученных и хорошо зарекомендовавших себя структур данных для хранения и работой с очередью с приоритетом являются Бинарная Куча (Binary Heap) и Куча Фибоначчи (Fibonacci Heap). Но данные структуры обладают некоторыми особенностями.
Например, бинарная куча для основных операций имеет трудоемкость Θ(logn), кроме нахождения минимального, а для слияния таких куч потребуется линейное время (!). Зато для хранения такой кучи необходимо мало памяти по сравнению с другими кучами.
Куча Фибоначчи обладает балансировкой при извлечении узла из кучи, что позволяет сократить трудоемкость основных операций. При большом количестве последовательных операций добавления Фибоначчиева куча растет в ширину и балансировка происходит лишь при операции удаления минимума, поэтому операция получения минимума может потребовать значительных затрат времени!
Решением над этой проблемой занялся Тадао Такаока (Tadao Takaoka), опубликовав свою работу «2-3 heap» в 1999 году…
Немного о структуре «2-3 Heap»
2-3 куча (2-3 heap) — это структура данных типа дерево, которая удовлетворяет свойству кучи (min-heap, max-heap). Является альтернативой кучи Фибоначчи (Fibonacci heap). Состоит из 2-3 деревьев.
Решение, которое предлагает 2-3 heap, заключается в том, что в отличии от Кучи Фибоначчи, 2-3 куча выполняет балансировку не только при удалении, но и при добавлении новых элементов, снижая вычислительную нагрузку при извлечении минимального узла из кучи.
Количество детей вершины t произвольного дерева T назовем степенью (degree) этой вершины, а степенью дерева назовем степень его корня.
2-3 деревьями называются деревья T0, T1, T2, ..., определенные индуктивно. Дерево T0 состоит из единственной вершины. Под деревом Ti понимается дерево, составленное либо из двух деревьев Ti-1 либо из трех: при этом корень каждого следующего становится самым правым ребенком корня предыдущего.
Деревьями 2-3 кучи назовем деревья H[i]. Дерево H[i] — это либо пустое 2-3 дерево, либо одно, либо два 2-3 дерева степени i, соединенные аналогично деревьям Ti.
2-3 куча – это массив деревьев H[i] (i=0..n), для каждого из которых выполняется свойство кучи.
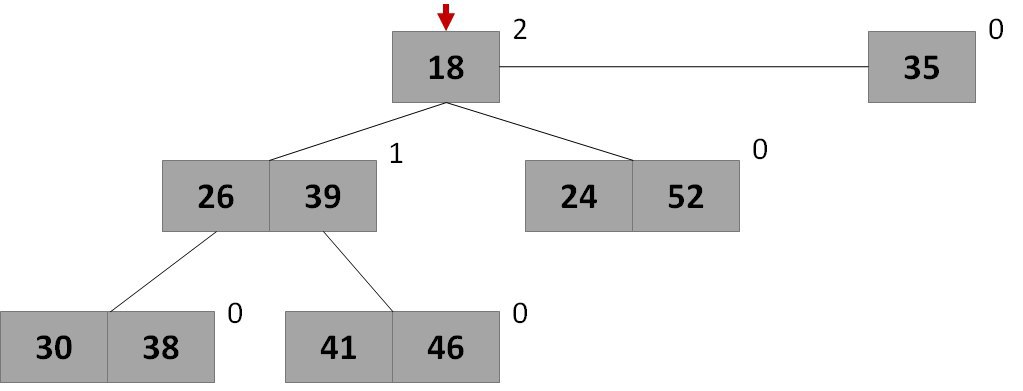
рис. Визуальное представление кучи
Структура узла
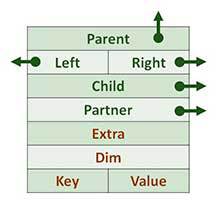
|
Каждый узел имеет указатели на другие узлы (поля имеющие стрелки), служебные поля и пара ключ (приоритет) – значение. |
Основные операции
Поиск минимального в 2-3 heap (FindMin)
Минимальный элемент кучи находится в корне одного из деревьев кучи. Чтобы найти минимальный узел, нужно пройтись по деревьям.
Поддерживая указатель на минимальный узел в куче мы можем находить этот узел за константное время ( Θ(1) )
Вставка в 2-3 heap (Insert)
- Для добавления нового элемента создадим дерево H[0] содержащее одну вершину
- Произведем операцию добавления этого дерева в кучу. При добавлении дерева степени i в кучу возможны следующие варианты:
- Если дерева с таким приоритетом нет, то просто его добавляем в кучу.
- Иначе извлекаем такое дерево из кучи и соединяем с добавляемым, после добавляем полученное дерево в кучу
- После добавление поправляем указатель на минимальный корень
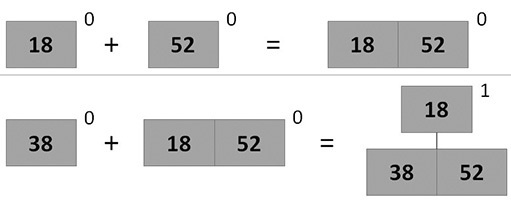

рис. Анимация последовательного добавления элементов в 2-3 кучу
Удаление минимального элемента из кучи
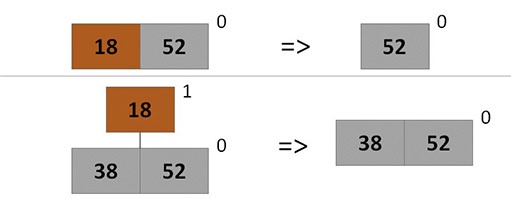
Минимальный элемент кучи находится в корне одного из деревьев кучи, допустим в H[i] – найдем его с помощью FindMin. Извлечем дерево H[i] из кучи и удалим его корень, при этом дерево распадется на поддеревья, которые мы впоследствии добавим в кучу.
Будем удалять корень рекурсивно: если дерево состоит из одной вершины, то просто удалим её; иначе отсоединяем от корня самого правого ребенка и продолжим удаление.
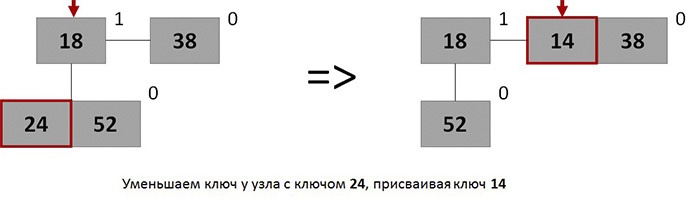
Уменьшение ключа у элемента
Первым делом мы можем свободно уменьшить ключ у необходимого узла. После этого необходимо проверить: если узел находится в корне дерева, то более ничего делать не нужно, иначе нужно будет извлечь этот узел со всеми поддеревьями и вставить его обратно в кучу (с уже измененным ключом).
Объединение двух куч в одну
Имеется две кучи, которые нужно объединить в одну. Для этого мы будем по очереди извлекаем все 2-3 деревья из второй кучи и вставлять их в первую кучу. После нужно будет поправить счетчик количества узлов: суммируем количество элементов в первой и во второй куче и записываем результат в счетчик в первой куче, а во второй куче устанавливаем счетчик в 0.
Сравнение трудоемкостей операций с другими алгоритмами
В таблице приведены трудоемкости операций очереди с приоритетом (в худшем случае, worst case)
Символом ‘*’ отмечена амортизированная сложность операций
| Операция | Binary Heap | Binomial Heap | Fibonacci Heap | 2-3 Heap |
|---|---|---|---|---|
| FindMin | Θ(1) | O(logn) | Θ(1)* | Θ(1)* |
| DeleteMin | Θ(logn) | Θ(logn) | O(logn)* | O(logn)* |
| Insert | Θ(logn) | O(logn) | Θ(1)* | Θ(1)* |
| DecreaseKey | Θ(logn) | Θ(logn) | Θ(1)* | Θ(1)* |
| Merge/Union | Θ(n) | Ω(logn) | Θ(1) | Θ(1)* |
Спасибо за уделенное внимание!
Исходный код реализации на C++, основанной на статье автора 2-3 Heap доступен на GitHub под MIT.
PS: При написании курсового проекта по этой теме, я понял, что информации в Рунете практически нет, поэтому решил внести свои пару копеек в это дело, рассказав заинтересованному сообществу об этом алгоритме.
Автор: biziwalker