Перевод поста Виталия Каурова (Vitaliy Kaurov) "Modeling a Pandemic like Ebola with the Wolfram Language".
Выражаю благодарность за помощь в переводе участникам сообщества ВКонтакте Русскоязычной поддержки Wolfram Mathematica: Еве Фрумен, Курбану Магомедову, Глебу Михновцу, Андрею Кротких.
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь (архив, ~100 МБ).
Данные крайне важны для беспристрастного взгляда в будущее, но одни только данные еще не являются прогнозом. Для предсказания развития пандемий, террористических актов, природных катастроф, падений рынков и других сложных явлений нашего мира необходимы научные модели. Один из инструментов борьбы с текущей ужасающей вспышкой лихорадки Эбола — создание компьютерной модели возможного распространения вируса. Понимая, где и как быстро вспышка может проявиться, правительственные структуры смогут организовать эффективные профилактические меры для снижения скорости передачи и, в конечном итоге, остановить эпидемию. Наша цель сейчас: продемонстрировать построение математической модели, описывающей глобальное распространение пандемии на основе реальных данных. Модель применима к любой эпидемии, но мы будем иногда упоминать и использовать данные о текущей вспышке лихорадки Эбола в качестве примера. Результаты не следует рассматривать как реалистичную количественную оценку текущей пандемии вируса Эбола.
Показать нам всем науку о вычислении пандемий я попросил доктора Марко Тиела (Dr. Marco Thiel), который уже разместил описание различных моделей распространения лихорадки Эбола на форуме Wolfram Community (где читатели могут принять участие в дискуссии). Мы работали вместе над программной реализацией приведенной ниже модели глобального распространения пандемий. Это задача стала значительно проще, благодаря новым инструментам, добавленным недавно в язык программирования Wolfram Language (систему Mathematica 10). Марко — прикладной математик, специализирующийся на теоретической физике и динамических системах. Его научно-исследовательская работа освещалась на BBC News и, благодаря своему прикладному математическому характеру, она затрагивает очень разные области: от устойчивости Солнечной системы до схем брачного поведения жуков-светлячков, криминалистической математики и многих других областей. Работая с таким широким кругом реальных задач, Марко, его коллеги и студенты из университета г. Абердина сделали технологии Wolfram частью своей жизни. Например, основная часть программы для этого блога написана Индией Брукнер (India Bruckner), очень талантливой школьницей из абердинской школы св. Маргариты для девочек, с которой Марко работал над летним проектом.
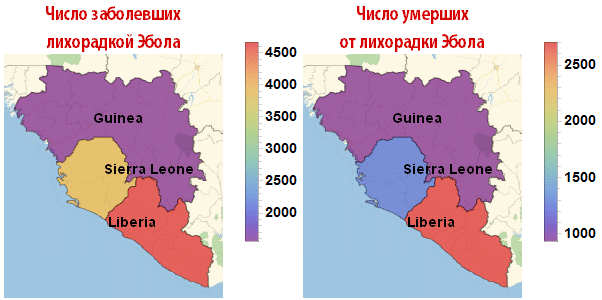
По мнению The New York Times, текущая вспышка лихорадки Эбола стала «самой беспощадной, затмившей собой вспышку 1976-го года, когда вирус был обнаружен». Согласно данным от 27 октября 2014 г. по меньшей мере 18 человек получили или получают сейчас лечение в Европе и Америке, в основном это медработники и сотрудники гуманитарных миссий, подхватившие вирус лихорадки Эбола в Западной Африке и вернувшиеся домой для лечения. Согласно отчету Центра по контролю и профилактике заболеваний США (CDC), обнародованному в сентябре, в самом худшем случае число заболевших лихорадкой Эбола превысит миллион человек в течение четырех месяцев. Лекарств или вакцин против вируса, одобренных Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) пока не существует, что приводит к летальному исходу в 60-90% случаев и распространению заболеванию через контакт с различными физиологическими жидкостями инфицированных людей. Ниже показано то, как выглядит ситуация в очаге пандемии в Западной Африке сейчас по данным The New York Times.
In[2]:=
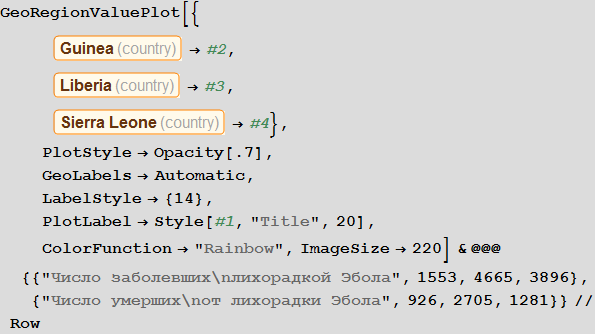
Out[2]=
Виталий: Марко, как вы думаете, математическое моделирование может помочь остановить пандемии?
Марко: Недавняя вспышка болезни, вызываемой вирусом Эбола, (БВВЭ) показывает, как быстро болезни могут передаваться между людьми. Угроза, конечно, не ограничивается БВВЭ. Существует большое число возбудителей инфекций, как например, различные типы гриппа (H5N1, H7N9, etc.), которые могут стать причиной пандемии. В виду этого, математическое моделирование путей передачи (болезней) становится еще более значимым. Представители власти от медицины должны принять решения, как противостоять угрозе. Есть большое число научных статей по этой теме, как например недавняя публикация Дирка Брокманна (Dirk Brockmann) в Science, доступная здесь. Профессор Брокманн также сделал несколько видео для иллюстрации исследований. Видео доступно на YouTube (часть 1, часть 2, часть 3). Было бы интересно повторить некоторые результаты из этой статьи и в целом исследовать вопрос с помощью Mathematica.
Виталий: Как же построить модель, описывающую распространение заболевания?
Марко: Подробно описанные модели, как например GLEAMviz, доступны онлайн, и могут быть использованы всеми, кто интересуется проблемой. Упомянутая модель, как и другие аналогичные ей, имеет 3 уровня: (1) модель эпидемии, описывающую передачу заболевания в гипотетической однородной популяции; (2) данные о популяции, такие как распределение и плотность населения; (3) уровень, описывающий миграции населения. Я использовал аналогичную модель, опираясь на мощные алгоритмы Mathematica: встроенные базы данных и широкие возможности импорта данных. Кроме того, алгоритмы визуализации Mathematica допускают разработку новой модели распространения заболеваний. Достоинствами самостоятельного моделирования являются полный контроль над программой и её изменением в соответствии с нашими требованиями. Курируемые данные Wolfram, доступные в Mathematica, являются очень удобной отправной точкой моделирования и могут быть дополнены данными, импортированными из внешних источников. Это одно из воплощений идей Конрада Вольфрама (Conrad Wolfram) об общедоступности вычисляемых данных. Используя текущие средства Mathematica, мы сможем представить себе те возможности, которые откроются нам после того, как все государственные/общественные данные станут вычисляемыми.
Существуют различные типы эпидемиологических моделей. Дальше мы, главным образом, будем использовать так называемую SIR-модель (от англ. Susceptible Infected Recovered). Популяция моделируется индивидуумами трех типов (тремя «ящиками»): здоровые индивидуумы из группы риска или восприимчивые индивидуумы (Susceptible), которые могут подхватить заболевание через контакт с уже инфицированными (Infected); выздоровевшие и переставшие распространять болезнь индивидуумы (Recovered).

Для моделирования вспышки с помощью языка Wolfram Language нам понадобятся уравнения, описывающие количество людей в каждой из этих категорий как функции времени. Мы будем использовать сначала уравнения с дискретным временем. Полагая, что существуют только три, не взаимодействующие между собой, категории индивидуумов, мы можем записать следующее:
In[3]:=
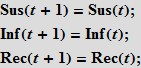
Эти уравнения означают, что число (в процентном отношении) восприимчивых/инфицированных/выздоровевших (Susceptibles/Infected/Recovered) в момент времени t+1 равно этому же числу в момент времени t. Предположим, что случайный контакт инфицированного индивидуума с восприимчивым приводит к новому заражению с вероятностью b; вероятность контакта пропорциональна числу восприимчивых индивидуумов (Sus), а также числу уже инфицированных (Inf). Это предположение означает, что люди уходят из «ящика» восприимчивых и переходят в «ящик» (категорию) инфицированных.
In[6]:=
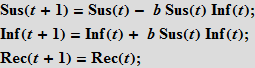
Далее мы полагаем, что люди выздоравливают с вероятностью c; выздоровление пропорционально числу больных людей; так, чем больше заболевших, тем больше выздоровевших.
In[9]:=
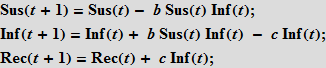
Нам также понадобятся начальные данные о количестве (в процентах) людей в каждой из категорий. Обратите внимание, что члены в правой части системы, характеризующие взаимодействие между категориями, всегда дают в сумме ноль, так что общий размер популяции не меняется. Если мы возьмем начальные значения так, что их сумма будет равна единице, то размер популяции всегда будет равен единице. Это важное отличительное свойство модели. Каждый человек должен быть отнесен к одному из трех «ящиков»; мы будем тщательно контролировать сохранение этого свойства для SIR-модели на графах, которую мы опишем ниже! В то же время существует определенная свобода в интерпретации этих трех «ящиков». Так, в нашем последнем примере мы будем учитывать летальные исходы. Кажется логичным считать, что умершие «покидают» нашу популяцию. Для сохранения размера популяции постоянным, что важно в нашем представлении, мы используем простой прием: будем рассматривать последнюю группу выздоровевших (Rec), как множество, содержащие людей, действительно перенесших болезнь, и умерших. Вполне разумно предположить, что ни умершие, ни выздоровевшие не смогут заразить остальное население, т.е. они инертны по отношению к нашей модели. Наше простое предположение будет заключаться в том, что некоторый фиксированный процент людей из Rec группы перенесли болезнь (выжили), а остальных будем считать умершими. Таким образом, мы включаем умерших в нашу модель, так что они не покидают группы, и мы не рассматриваем рождения новых людей. Это обеспечивает сохранение размера популяции постоянным.
Вот простейшая реализация SIR-модели, позволяющая вам изменять параметры:
In[12]:=

Out[12]=
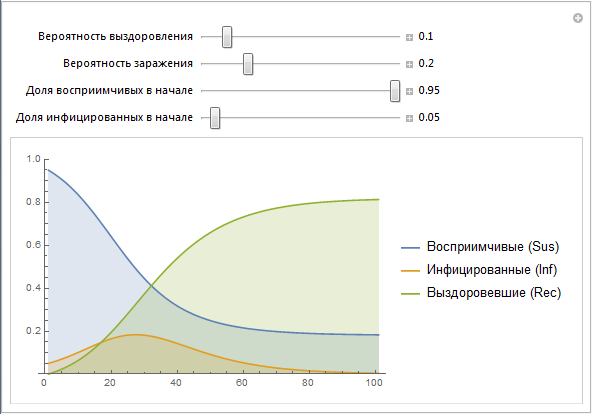
Мы используем векторы значений Sus, Inf, Rec, которые строятся рекурсивно. Позже мы создадим более простую реализацию этой конструкции. Заметим, что параметры b и c содержат в себе множество эффектов, которые на этом этапе напрямую не смоделированы. Например, вероятность заражения b действительно описывает риск заражения, но в тоже время она зависит от поведения людей (большое количество массовых мероприятий, общественных мест и т. п. может привести к увеличению вероятности заражения, как это часто происходит, скажем, в учебных заведениях), плотность населения (высокая плотность населения может привести к большей вероятности заражения). Вероятность выздоровления c зависит от таких вещей как: качество здравоохранения, доступностью врачей и так далее. Позже мы попробуем смоделировать некоторые из вышеперечисленных факторов.
Хотя SIR-модель вероятно не самая подходящая для описания вспышки лихорадки Эбола, но тем не менее, эта модель не так далека от истины. Люди инфицируются через телесный контакт; категория выздоровевших может рассматриваться из процента выживших и умерших людей, если мы предположим, что повторное заражение маловероятно. В различных странах и при различных обстоятельствах доля выздоровевших/умерших сильно меняется — кое что из этого мы смоделируем позднее.
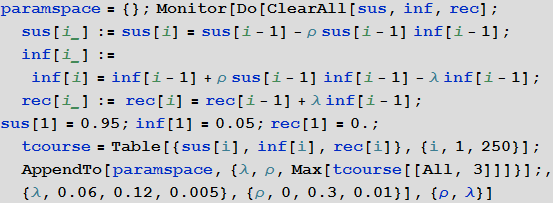
Более систематическим способом изучения SIR-модели является изучение так называемого пространства параметров модели. Мы можем визуализировать в зависимости от параметров множество различных характеристик, например, наибольшее количество заболевших, общее число заболевших в ходе вспышки заболеваемости от вируса. Оси диаграммы представленной ниже показывают вероятности заражения и выздоровления, при этом цвет на диаграмме характеризует процент зараженных людей.
In[13]:=
In[14]:=

Out[14]=
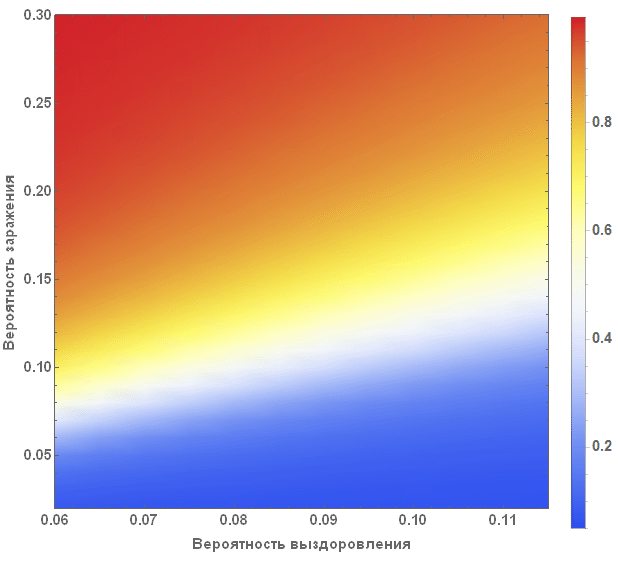
Из диаграммы явно видно, что при маленьких значениях вероятности выздоровления и больших значениях вероятности заражения, больными оказывается более 90% людей, при этом, в противоположной ситуации, зараженными являются около 5% людей, что соответствует их начальному числу.
Виталий: Для перехода от чистой математики к моделированию процессов, происходящих в реальном мире, нам потребуются данные, скажем о популяциях людей и их географическом положении. Каким образом мы можем получить эти данные?
Марко: Мы будем объединять несколько различных подпопуляций воедино (например, аэропорт, город, страна и т. д.) и изучим распространение болезни между ними. Каждая из этих подпопуляций может быть смоделирована как SIR-модель. Когда мы начнем объединять подпопуляции, их индивидуальные размеры будут играть ключевую роль. Данные о численности населения, как и многие другие виды данных, встроены напрямую в Mathematica, что позволяет достаточно легко использовать их в нашей модели.
Мы будем использовать встроенные данные для улучшения качества нашей модели и доведения ее до логического завершения, но в начале мы можем использовать международную сеть аэропортов для моделирования процесса передачи болезни. Для этого нам понадобится список всех аэропортов и воздушных путей. На сайте openflights.org вы можете найти всю необходимую информацию. Я сохранил ее в файлы «airports.dat» и «routes.dat.»
Виталий: Мы могли бы использовать функционал семантического импорта данных для работы с внешними данными. Функция SemanticImport может импортировать файл семантически, предоставляя на выходе объект Dataset. Dataset и Association — являются новыми функциями, дающими возможность создания структурированных баз данных в Mathematica. Dataset может представлять собой не только прямоугольные многомерные массивы данных, но и деревья произвольного вида, соответствующие данным с произвольной иерархией. Dataset позволяет очень легко получить доступ к любым данным в базе и производить их обработку, поэтому мы будем ее активно использовать. Незначительная часть данных, находящихся в файле airports.dat была убрана для более точной работы функций семантического импорта. Все файлы прикреплены в начале этой статьи, вместе с документом Mathematica.
Марко: Да, действительно, функция SemanticImport очень мощная. В моей первой попытке моделирования я использовал функции Import и Intrepreter, обе также очень мощные. Затем мне пришлось провести большую «очистку» данных — что, в целом, является стандартной многошаговая процедурой, которую приходится выполнять, если имеешь дело с внешней невычисляемой информацией. Но благодаря использованию функции SemanticImport, я смог сделать код программы коротким и более читаемым.
In[15]:=

Out[15]=
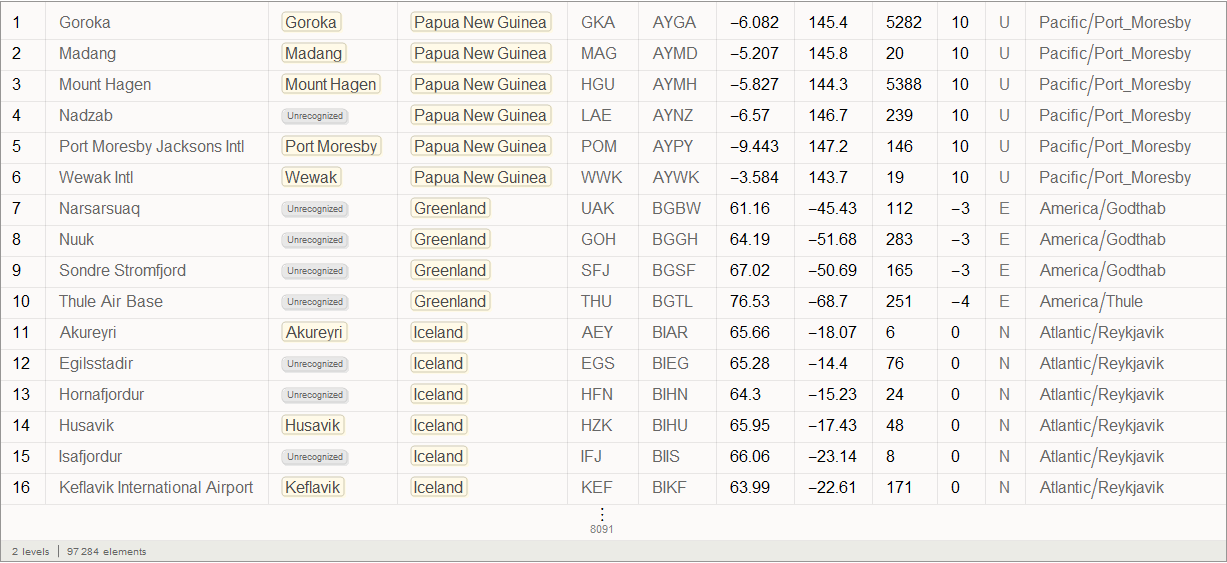
In[16]:=
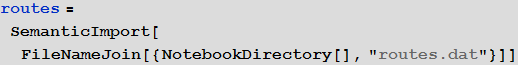
Out[16]=
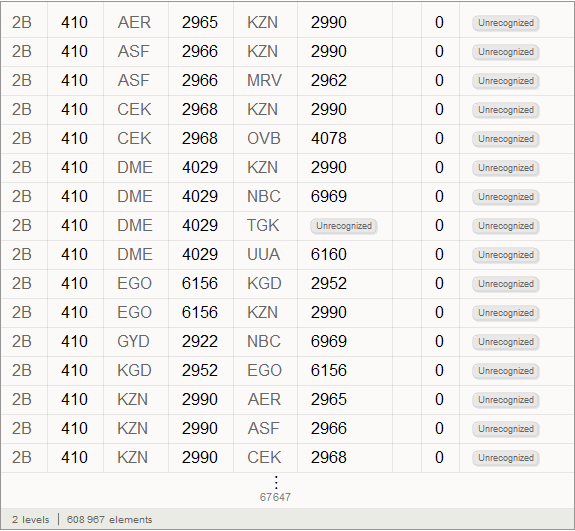
Виталий: Полученные после работы функции обведенные оранжевой рамкой объекты со светло-оранжевым фоном представляют собой так называемые Entity, появившиеся в Mathematica 10. Они представляют собой, по сути, ключи централизованного доступа к базам данных Wolfram|Alpha.
In[17]:=
![]()
Out[17]=

Так, мы видим, что функция SemanticImport автоматически классифицировала третий и четвертый столбцы данных, как города и страны, представив их в виде объектов Entity.
Марко: Теперь мы можем отобразить все аэропорты Мира.
Виталий: Действительно, с новыми возможностями, предоставляемым функциями подъязыка географических вычислений, в частности, с помощью функции GeoGraphics и многочисленных ее опций, таких как GeoBackground, GeoProjection и GeoRange, мы можем создать изображение, которое позволит легко отобразить большой массив данных.
In[18]:=
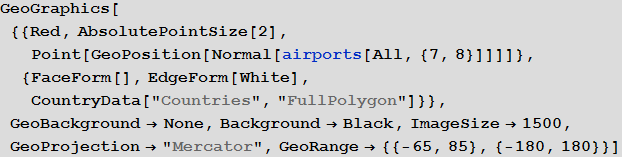
Out[18]=
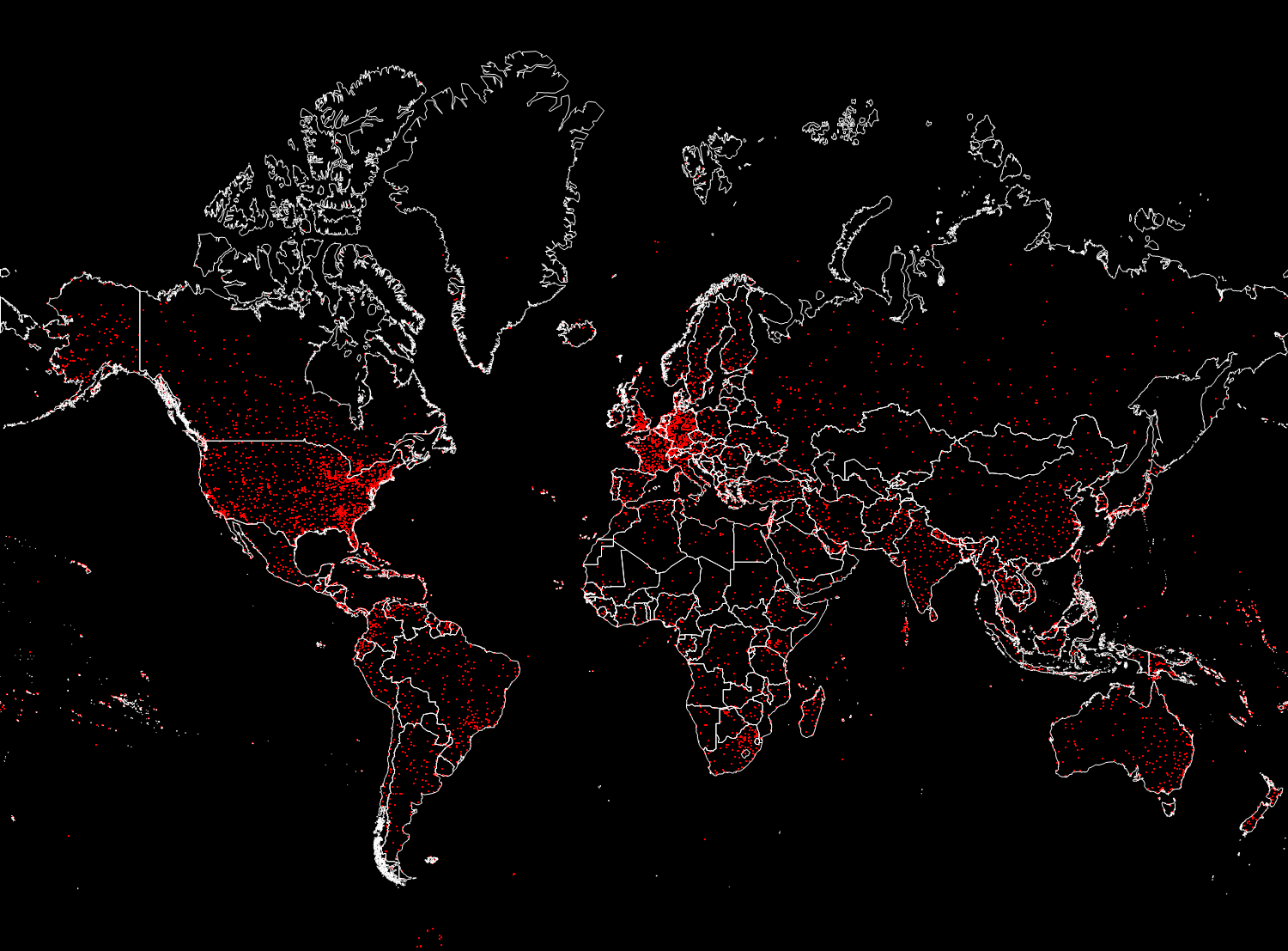
Пятый столбец в базе airports представляет собой это трехбуквенный идентификатор IATA (Международная ассоциация воздушного транспорта). Эти идентификторы потребуются нам для задания маршрутов между аэропортами, которые хранятся во второй базе данных. Не все записи в базе airports имеют их, скажем, ниже вы можете видеть значения 100 последних записей базы из соответствующего столбца.
In[19]:=
![]()
Out[19]=
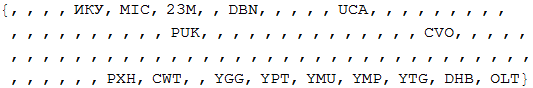
Некоторые из них некорректны ввиду того, что содержат цифры. Мы очистим наши данные, удалив записи с некорректным или отсутствующим идентификатором IATA. Ниже можно видеть количество записей в исходной базе данных.
In[20]:=
![]()
Out[20]=
![]()
Теперь очистим базу данных и перезапишем ее. Число ниже показывает, опять же, количество записей, но уже в обновленной базе данных.
In[21]:=

Out[22]=
![]()
Марко: Теперь мы создадим список правил, связывающих идентификаторы аэропортов и их геокоординаты.
In[23]:=

Виталий: Мы использовали функцию Dispatch, которая создает оптимизированное представление списка правил замены, что никак не влияет на получаемые результаты, но позволяет работать с длинными списками намного быстрее.
Марко: Теперь мы можем проанализировать связи между аэропортами. Число ниже показывает общее их количество.
In[24]:=
![]()
Out[25]=
![]()
Не каждый идентификатор IATA имеет геокоординаты, поэтому очистим список связей между аэропортами, удалив связи без информации о геокоординатах аэропортов.
In[26]:=
![]()
Out[27]=
![]()
В целом получилось 67 210 связей. На рисунке ниже мы отобразим только 15 000 случайно выбранных из них, для того, чтобы на можно было разобрать основные направления перелетов.
In[28]:=

Out[28]=
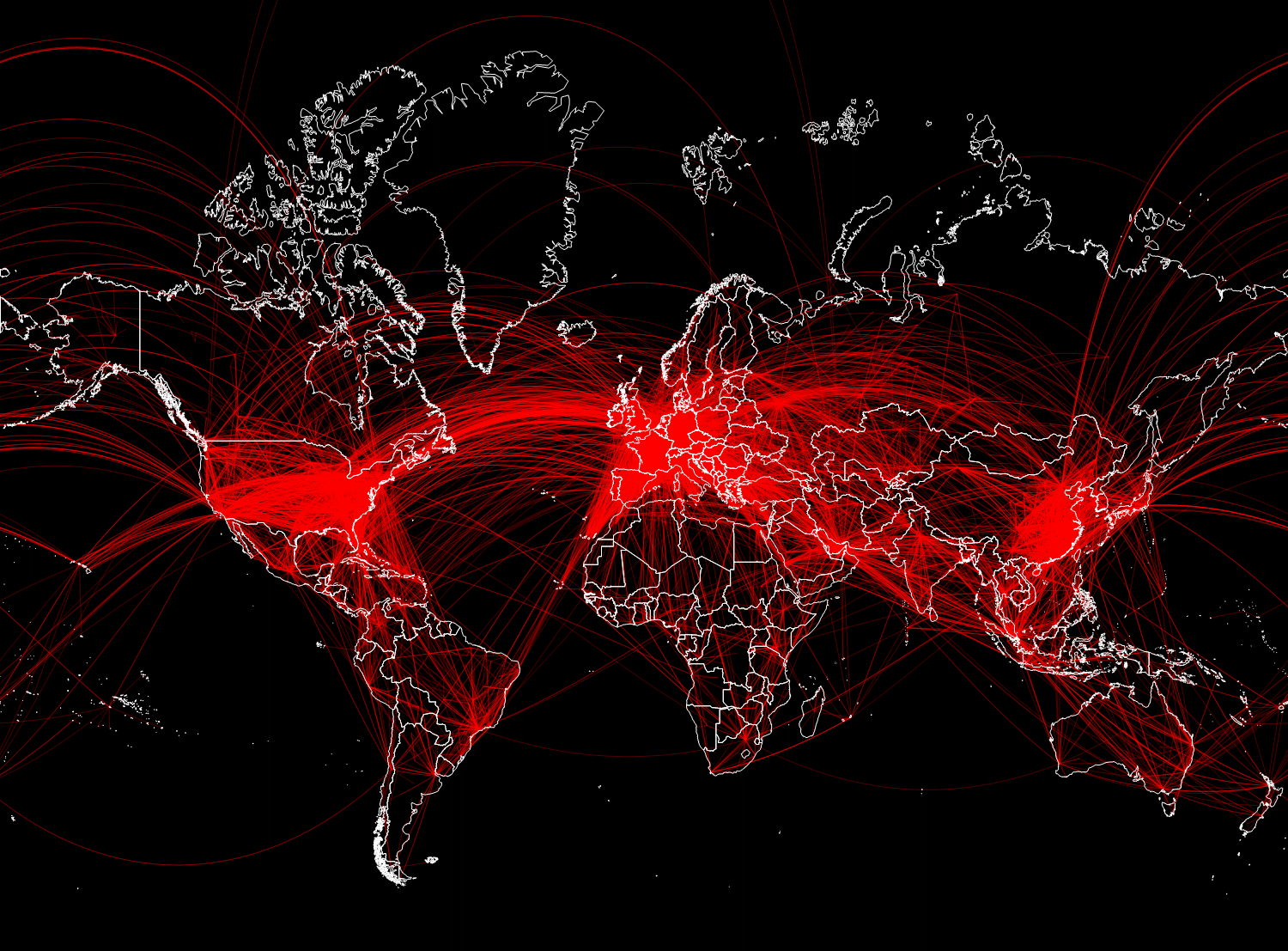
Виталий: Теперь, когда у нас есть данные, как интегрировать их в математические модели?
Марко: Нам нужно описать пути перемещения популяции. Мы будем использовать глобальную сеть воздушного транспорта для построения первой модели пандемии. Мы будем рассматривать перелеты, как связи между различными областями. Эти области можно рассматривать, как «популяционные бассейны» соответствующих аэропортов.
Виталий: Можно использовать функцию Graph для быстрого и эффективного создания графов. Существует множество различных связей между одними и теми же аэропортами, поэтому полученный граф будет мультиграфом, в последней версии Wolfram Language как раз был добавлен функционал для работы с ними. Для упрощения начальной модели, мы будем учитывать только сам факт связи между двумя аэропортами, создавая одно ребро графа, если имеется хотя бы один маршрут, соединяющий две вершины. Позже, в усовершенствованной модели, мы уже будем использовать мультиграфы.
In[29]:=
![]()
В полученном графе вершины соответствуют аэропортам с различными идентификаторами IATA.
Из результата вычисления кода ниже видно, что в этом графе существует несколько компонент связности, при этом существенный размер имеет только первая из компонент. Мы удалим компоненты с небольшим числом вершин, так как они не сильно влияют на динамику в целом.
In[30]:=
![]()
Out[30]=
![]()
In[31]:=

In[32]:=
![]()
Out[32]=
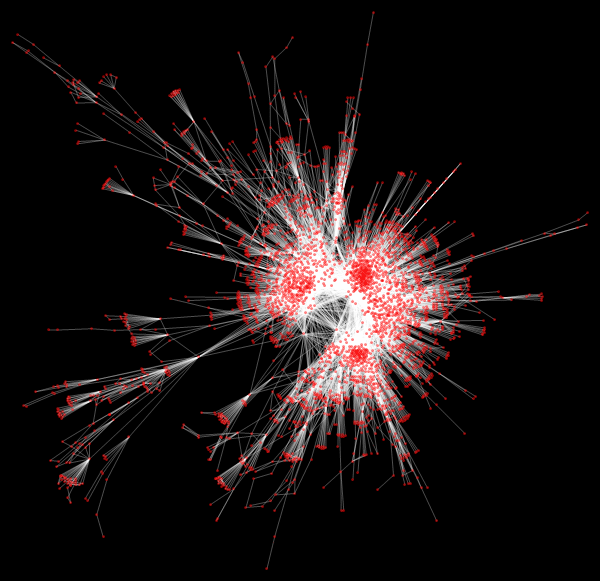
Построим для нашего графа матрицу смежности.
In[33]:=
![]()
Out[34]=
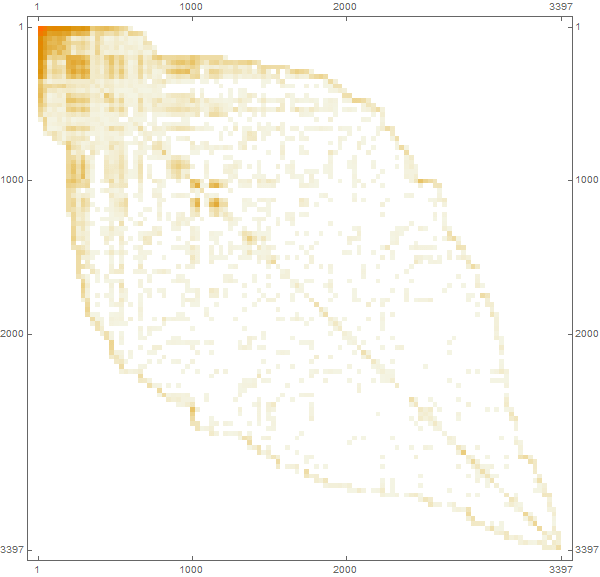
Марко: Элемент матрицы с индексами (i, j) будет нулевым, если аэропорты i и j не связаны между собой, в противном случае единичным. Объединенная матрица автоматически конвертируется в форму представления разреженных массивов SparseArray для более эффективных вычислений и использования памяти. Мы также можем использовать «размер популяции» как характеристику каждого аэропорта, что по сути будет соответствовать емкости популяционного бассейна аэропорта. Затем мы попытаемся сделать более разумные предположения относительно численности населения, но сейчас, ради упрощения, мы считаем ее одинаковой для каждого отдельно взятого аэропорта.
In[35]:=
![]()
Теперь нам предстоит довольно сложный шаг. Нам необходимо определить параметры, использующиеся в нашей модели. Проблема состоит в том, что каждый из них «параметризует» множество эффектов и ситуаций. Для нашей модели, нам необходимы:
• Вероятность заражения. Это фактор, который определяет в нашей модели, насколько вероятно, что контакт приводит к инфекции. Этот фактор, безусловно, зависит от многих вещей: плотность населения, местные поведения людей, санитарного просвещения, и так далее. Чтобы запустить нашу модель, мы выберем следующее значение этой вероятности для всех аэропортов:
In[37]:=
![]()
• Вероятность выздоровления. Она будет очень сильно зависеть от типа заболевания и качества системы здравоохранения. Она также будет зависеть от того, каждый ли человек имеет доступ к медицинскому страхованию. В странах, где только часть населения имеет доступ к высококачественной медицинской помощи, болезни, как правило, распространяются быстрее. Для нашей начальной модели, мы установим следующее значение для всех аэропортов:
In[38]:=
![]()
С помощью этих двух параметров мы по сути задали модель эпидемии. Но мы по-прежнему нуждаемся в еще одном параметре.
• Коэффициент миграции. Это коэффициент пропорциональности, который описывает склонность определенного населения (в популяционном бассейне аэропорта) путешествовать. В этой модели, мы взяли его постоянным, но это конечно также зависит от финансовой ситуации в той или иной стране и других факторов. Он описывает, грубо говоря, процент людей в стране или регионе, которые путешествует. Мы не используем мульти-агентную модель которая описывает индивидуальное движение людей. Мы используем ячеечную модель популяции (compartmental population model), в рамках которой, по сути, мы описываем просто процент населения, который путешествует. Мы (по крайней мере, в конце поста, где будет произведено моделирование с учетом особенностей стран) будем также учитывать различные размеры популяций, структуру мультиграфа, а также количество полетов, совершаемых между странами. Используя матрицу связей (она же матрица смежности графа), мы не будем рассматривать миграцию отдельных людей между различными аэропортами. Мы будем вначале использовать общий коэффициент миграции (одинаковый для всех), который мы зададим таким:
In[39]:=
![]()
Еще одно довольно важное предположение состоит в том, что мы будем использовать — в начале — один и тот же коэффициент миграции для всех трех категорий: восприимчивых, инфицированных и выздоровевших. В действительности зараженные, особенно в инфекционной фазе, когда у них уже начинают проявляться симптомы заболевания, будут осуществлять миграции иначе. Кроме того, мобильность населения будет отличаться в разных странах, при этом она, безусловно, будет зависеть также и от расстояния, которое необходимо преодолеть людям. Мы позже выберем более реалистичные параметры.
Теперь инициализируем нашу модель полагая, что вначале во всех городах есть только восприимчивые к инфекции и нет зараженных или выздоровевших:
In[40]:=
![]()
Теперь мы должны ввести 5% инфицированных в популяционный бассейн того аэропорта, с которого начнется распространение заболевания.
Виталий: Вспышка началась в Гвинее в декабре 2013 года, а затем вирус распространился на Либерию и Сьерра-Леоне. Согласно The New York Times, первой зараженной за пределами Западной Африки стала медсестра из Испании, которая заболела в сентябре во время лечения миссионера, зараженного в Сьерра-Леоне. После этого она была переправлена в госпиталь в Мадриде. Ниже приведен список аэропортов в Гвинее:
In[41]:=
![]()
Out[41]=
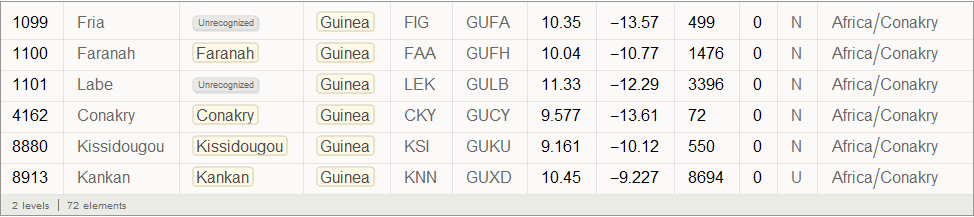
Найдем индекс вершины графа, соответствующий Международному аэропорту Конакри (его код CKY), который находится в крупнейшем городе и столице Гвинеи:
In[42]:=
![]()
Out[42]=
![]()
In[43]:=
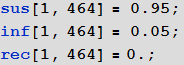
Марко: Прежде, чем мы запишем уравнения SIR-модели с членами, отвечающими за связи между областями, мы введем два объекта, первый — общее количество (потенциальных) пассажиров в каждом аэропорту:
In[46]:=
![]()
Второй объект — мы создадим на основе матрицы связей намного меньший по размеру список, который будет содержать для каждого аэропорта только список связанных с ним аэропортов:
In[47]:=
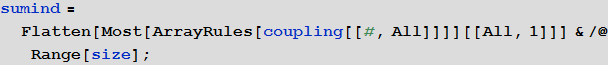
Этот список очень полезен, потому что матрица связей крайне разрежена, поэтому список sumind существенно ускорит вычисления. Теперь мы можем записать уравнения SIR-модели:
In[48]:=

Члены, отвечающие за связи между областями подсвечены оранжевым. По существу, мы вычисляем средневзвешенное число людей для каждого популяционного бассейна на основе всех соседних аэропортов. Существует множесво других вариантов записи этих членов.
Теперь мы запускаем итерационный процесс моделирования на основе этих рекуррентных уравнений и посмотрим сколько это займет времени:
In[50]:=
![]()
Out[50]=
![]()
Чтобы получить первое представление о решении, мы можем построить S, I и R кривые для некоторых 200 аэропортов:
In[51]:=
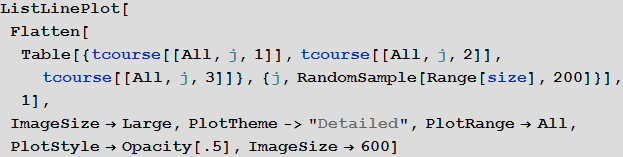
Out[51]=
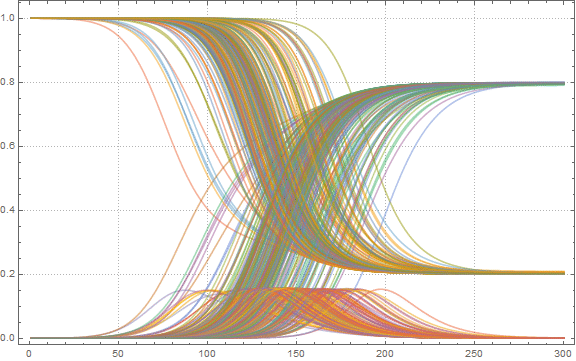
Теперь найдем максимальную долю больных людей среди всех аэропортов:
In[52]:=
![]()
Out[52]=
![]()
Создадим список координат аэропортов, упорядоченных в соответствии с их индексами в графе:
In[53]:=
![]()
Теперь можно посмотреть на то, как выглядит карта заражения для нескольких моментов времени:
In[54]:=
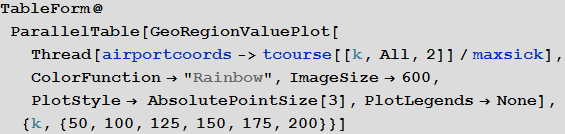
Out[54]//TableForm=
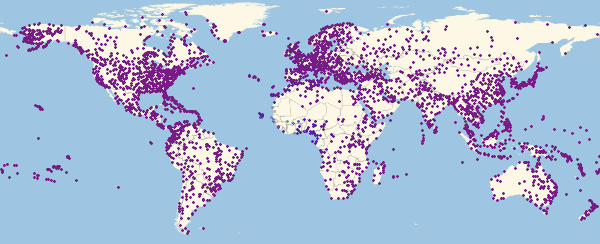
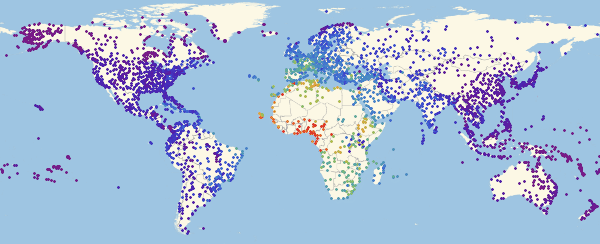
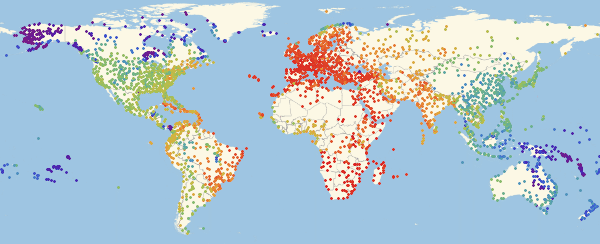
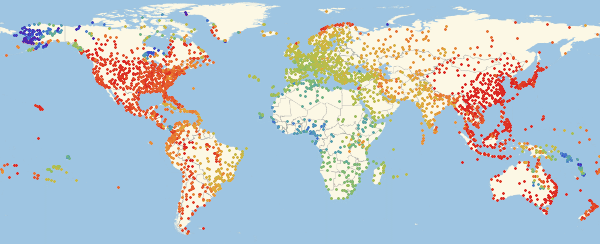
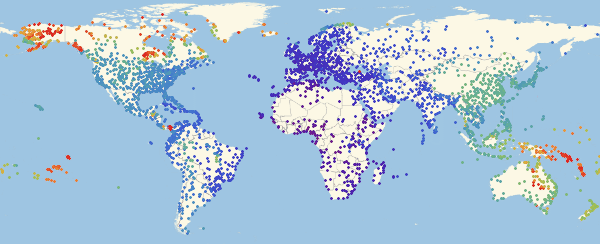
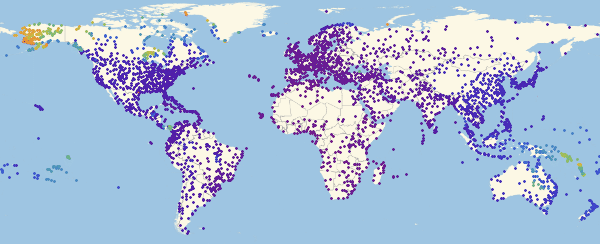
Здесь и ниже в подобных визуализациях, цвет означает долю зараженных (увеличение доли происходит при переходе от фиолетового к красному).
In[55]:=
![]()
Out[55]=
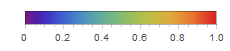
Обратите внимание, что есть три основных региона: Европа, которая заражается первой, затем Америка и Азия. Этот вид распространения болезни связан со структурой графа. Мы можем попробовать визуализировать это с помощью функции Graph.
Виталий: Алгоритмы кластеризации функции Graph помогут нам узнать, какие континенты способствуют распространению пандемии через авиаперевозки. Чтобы получить список континентов (см. ниже) воспользуемся новым подъязыком Entities. Для этого воспользуемся формой локального ввода, которая может быть получена с помощью сочетания клавиш CTRL + SHIFT + =, затем введем в нее запрос «continents» ![]() .
.
In[56]:=

Мы не будем рассматривать Антарктиду, поэтому исключим ее из этого списка, а затем построим базу данных, в которой будет храниться информация о принадлежности того или иного идентификатора аэропорта тому или иному континенту:
In[57]:=
![]()
In[58]:=

Out[58]=
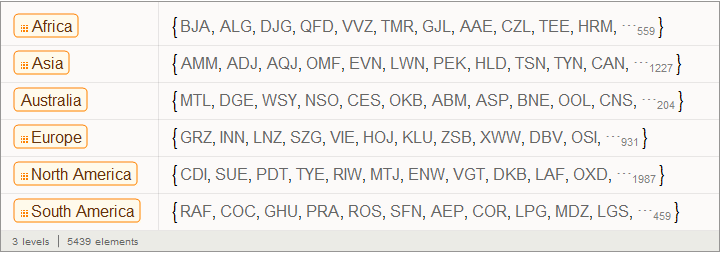
Функция, приведенная ниже, позволяет ответить на вопрос о том, какому из континентов принадлежит тот или иной идентификатор аэропорта:
In[59]:=

Применим эту функцию к некоторым идентификаторам:
In[61]:=
![]()
Out[61]=
![]()
В нашем графе есть большое количество тесно связанных друг с другом семейств вершин (аэропортов) (graph communities), которые при этом довольно сильно отличаются по численности:
In[62]:=
![]()
Out[63]=
Семейства вершин графа — это группа вершин, которая тесно связана внутри себя большим количеством объединяющих их рейсов, при этом семейства вершин связаны между собой отдельными, подчас одиночными, рейсами. Для того, чтобы не переполнить наш чертеж графа большим количеством неинформативных подписей, мы пометим только те семейства, число вершин в которых больше 60. Создадим подписи к семействам:
In[64]:=

Out[64]=

Теперь мы можем визуализировать структуру графа и увидеть, как главные центры осуществляют транспортировку к меньшим. В этом конкретном рисунке цвета не означают уровня заражения, а служат только лишь для цветовой дифференциации семейств:
In[65]:=
![]()
Out[65]=
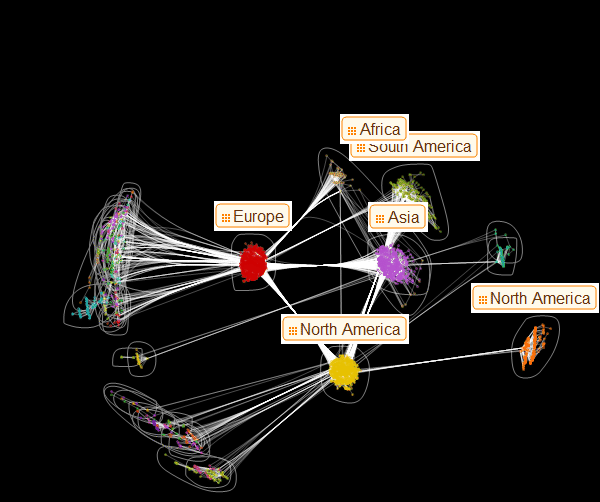
Марко: Из этого представления графа становится очевидным наличие трех доминирующих семейств вершин. Из этого рисунка также становится ясно, какое из этих основных семейств служит источник заражения меньших. Это может помочь в принятии решения о профилактических мерах по распространению эпидемии. Теперь мы можем создать граф, который похож на один, из представленных в статье Дирка Брокмана:
In[66]:=
![]()
In[67]:=

In[68]:=

Out[68]//TableForm=


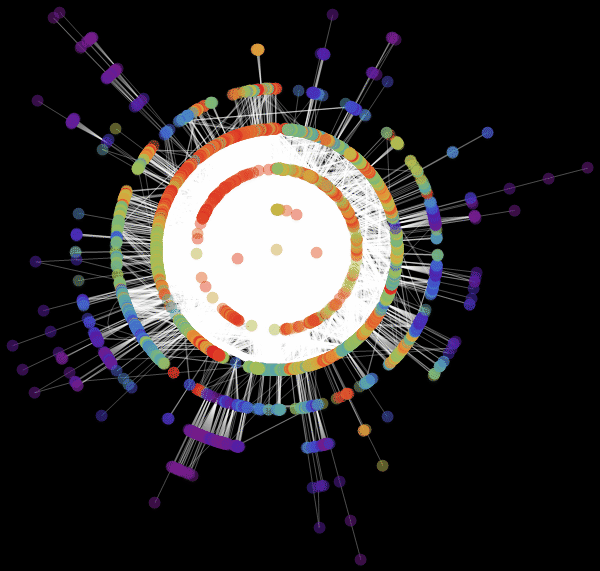
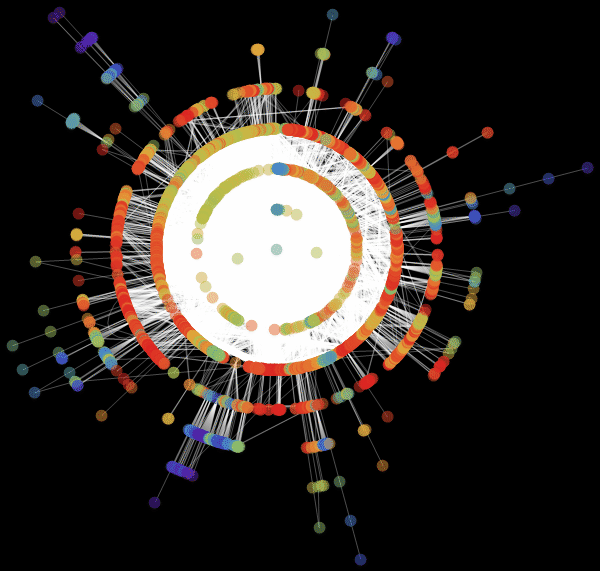
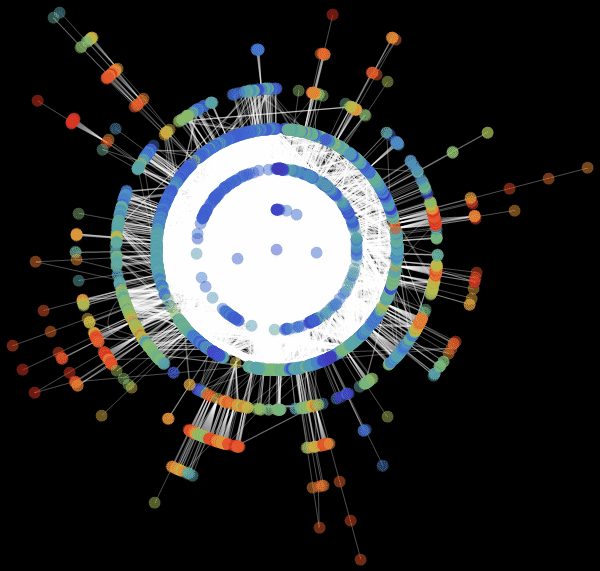
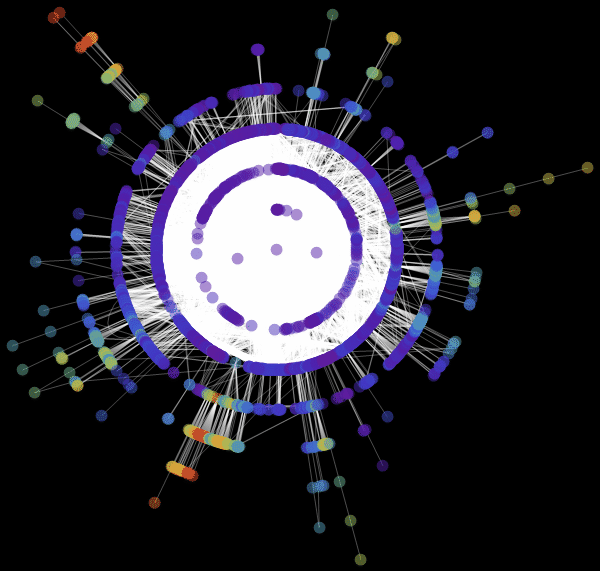
Виталий: Мы использовали значение «RadialEmbedding» для опции GraphLayout (радиальное расположение вершин графа) и установили значение подопции «RootVertex» (корневой вершины), равное «FNA», т. е. идентификатору аэропорта, с которого началось распространение эпидемии. Я вижу, что пандемия распространяется из этой вершины по слоям от центра к периферии. Марко, не могли бы вы объяснить, что это значит?
Марко: В центре нашей визуализации графа мы видим аэропорт, соответствующий началу вспышки заболевания. Слой вокруг него представляет собой все те аэропорты, которых можно достичь прямым перелетом, они становятся первыми жертвами распространяющейся эпидемии. Следующий слой представляет собой набор аэропортов, которые могут быть достигнуты с одной пересадкой, ясно, что они будут инфицированы на втором шаге распространения заболевания и т. д. Эта визуализация демонстрирует то, что структура сети, а не расстояние, имеет важное значение.
Виталий: Как можно сделать эту модель несколько более реалистичной?
Марко: Мы рассмотрели некоторые простые частные случаи модели, которая сначала описывает вспышку болезни с помощью SIR-модели на локальном уровне и затем объединяет множество аналогичных локальных SIR-моделей, основываясь на связях некоторого графа транспортных путей. Однако, все еще существует множество проблем, которые можно поставить. Вот их формулировки:
1. Вероятность передачи зависит от множества факторов, например, системы здравоохранения и плотности населения в регионе.
2. Вероятность выздоровления будет также зависеть от многих факторов, например, системы здравоохранения.
3. Не все возможные пути (дороги/траектории полета) будут выбираться с равной вероятностью. Опубликованные статьи свидетельствуют о том, что существует определенная зависимость: чем больше расстояние до места, тем меньше вероятность, что кто-то туда поедет.
4. Миграция/скорость перемещения будет своя для каждой из групп восприимчивых, инфицированных и выздоровевших; скажем, инфицированные люди вряд ли будут путешествовать.
Кроме того, нам может потребоваться учет в модели различных попыток правительств контролировать вспышку заболевания. Итак давайте попробуем решить некоторые из этих вопросов, создав новую модель пандемии лихорадки Эбола. Если бы мы попробовали учесть в модели все города и все аэропорты Мира, то это явно было бы слишком сложной задачей для обычного ноутбука. На основании приведенных выше разделов, в целом ясно, как можно расширить модель в этом направлении, но мне хотелось бы обратить внимание на некоторые дополнительные подходы, которые могут оказаться полезными.
Наша модель будет работать со всеми (по крайней мере с подавляющим большинством) стран по всему Миру. Связи между ними будут моделироваться на основе соответствующих связей между аэропортами. Начнем с того, что соберем некоторые дополнительные данные для нашей модели.
Очистим переменные и, как и прежде, импортируем данные о аэропортах и рейсах:
In[69]:=
![]()
In[70]:=

Функция SemanticImport сразу определяет страну, к которой принадлежит тот или иной аэропорт. Мы можем легко построить список правил замены вида «идентификатор аэропорта» > «страна»:
In[71]:=
![]()
Сейчас мы создадим граф с помощью функции Graph. Поскольку мы хотим изучить связи между странами, мы заменим идентификаторы аэропортов соответствующими названиями стран:
In[72]:=
![]()
Виталий: Вы говорите, что теперь ребра графа соответствуют связям между странами, а не аэропортами?
Марко: Ребра на самом деле задают, как и раньше, рейсы. Они, как и раньше, соединяют между собой аэропорты, но мы теперь хотим моделировать связи между странами. Поэтому, мы, проще говоря, заменяем все аэропорты, находящиеся в одной стране — одной вершиной, соответствующей этой стране. По сути мы решаем известную математическую задачу о стягивании ребер графа.
Оказывается, как и раньше, что данные по некоторым аэропортам отсутствуют, при этом большинство недостающих данных относится к крайне маленьким аэропортам. Мы удалим все аэропорты, страна расположения которых нам не известна:
In[73]:=
![]()
Наконец, что не менее важно, мы построим матрицу смежности (матрицу связей) нашего графа:
In[74]:=
![]()
Мы также создадим список всех стран, которые участвуют в нашей модели:
In[75]:=
![]()
Очевидно, что чем больше плотность населения, тем выше доля заболевших. Конечно, это допущение, так как важно учитывать именно места локальной повышенной населённости. Если страна очень большая, но все живут в городах, реальная плотность населения значительно выше.
Чтобы рассматривать население, нам нужна информация по её численности и плотности во всех странах:
In[76]:=

Теперь нужно построить простую «модель» описывающую, как плотность населения может влиять (отчасти) на количество заболевших. В первой модели мы приняли значение вероятности заражения равным ρ = 0.2. И это давало довольно «хорошие» результаты, в том смысле, что наблюдался ожидаемый характер распространения болезни. Мы хотим расширить модель, но без сильного изменения диапазонов параметров. Так что, «приемлемым» — в качестве первого приближения — будет выбрать значения параметров, находящихся в тех же пределах. В сущности, мы наблюдаем, что ключевыми параметрами являются λ и ρ (вероятности выздоровления и заражения, соответственно) Таким образом, мы хотим начать с приблизительно тех же значений, что и в первой симуляции.
Чтобы изменить параметр вероятности заражения с учетом плотности населения сперва рассмотрим гистограмму распределения плотности населения:
In[77]:=

Out[77]=
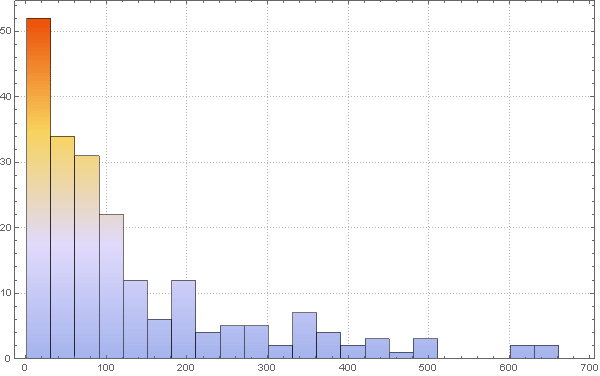
Также мы можем вычислить среднее значение плотности населения:
In[78]:=
![]()
Out[78]=
![]()
Примем допущение, что вероятность заражения увеличивается вместе с ростом плотности населения. Для «средней плотности населения» мы полагаем вероятность заражения, равной 0.2. Сделаем грубое предположение, что зависимость между этими величинами выражается в графике, приведенном ниже:
In[79]:=
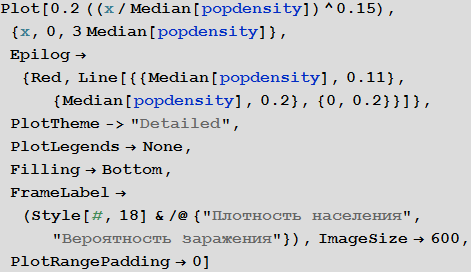
Out[79]=
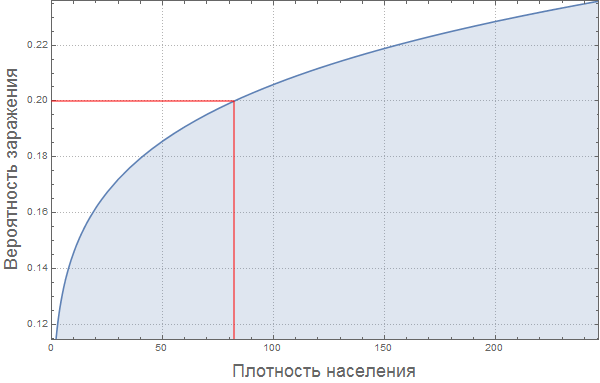
Рассчитаем долю зараженных для каждой из стран:
In[80]:=
![]()
Конечно, эта «модель» зависимости между долей зараженных и плотностью населения очень сыра. Возможно, читатель найдет способ улучшить её?
Виталий: Было бы интересно узнать некоторые закономерности, основанные на реальной информации о том, как вероятность заражения изменяется в зависимости от плотности населения. Неплохо было бы сделать эту закономерность переменным условием, чтобы читатели могли попробовать свои версии и понаблюдать изменения в симуляции. Возможно, следует принять во внимание феномен перколяции, когда происходит резкое увеличение доли заболевших, в том случае, если плотность населения достигает критических значений. Также возможен некий «эффект затухания» из-за городской инфраструктуры. Но это только мои предположения. Могли бы вы высказать ваше мнение на этот счет?
Марко: Если в ограниченном пространстве находится много людей, то вероятность заражения должна быть монотонно возрастающей. Также, я думаю важно отметить, что вероятность заражения не растет линейно, а ее производная уменьшается (функция выходит на «плато»). Вероятность заражения должна зависеть от расстояния до ближайшего соседа, поэтому она может расти как квадратный корень из плотности населения, что даст нам показатель степени 0.5. Но если движение отдельных людей уже будет ограничиваться их соседями, то скорость роста этой функции будет меньше, а значит мы получим показатель степень меньше 0.5. Это мое личное мнение. Статья "The scaling of contact rates with population density for the infectious disease models" by Hu et al., 2013, показывает, что наши предположения верны, по крайней мере для этой грубой модели.
Чтобы оценить вероятность выздоровления, сделаем еще одно смелое допущение. Предположим, что система здравоохранения лучше в тех странах, где выше ожидаемая продолжительность жизни. Чтобы построить эту подмодель, воспользуемся данными о ожидаемой продолжительности жизни, встроенными в Mathematica.
In[82]:=
![]()
Визуализируем распределение ожидаемой продолжительности жизни по странам в этой гистограмме:
In[83]:=
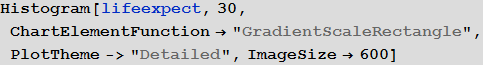
Out[83]=
Обратите внимание, что для нескольких стран информация отсутствует, так что возьмем для них значение ожидаемой продолжительности жизни в стандартные 70 лет. Это никак не повлияет на результаты, ввиду того, что эти страны (островные государства и Антарктика) по сути не играют роли в нашей модели.
Вычислим среднее значение ожидаемой средней продолжительности жизни:
In[84]:=
![]()
Out[84]=
![]()
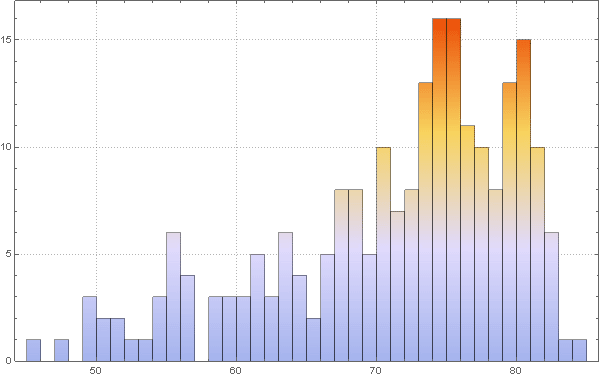
Теперь, как говорилось выше, сформулируем наше предположение, что ожидаемая продолжительность жизни является приблизительным показателем качества системы здравоохранения, которая, в свою очередь, является приблизительным показателем вероятности выздоровления. Опять же, это очень грубое допущение, потому что ситуация в таких относительно богатых странах как Испания и США показывает, что вероятность выздоровления может и не быть выше в странах с большим достатком:
In[85]:=

Out[85]=
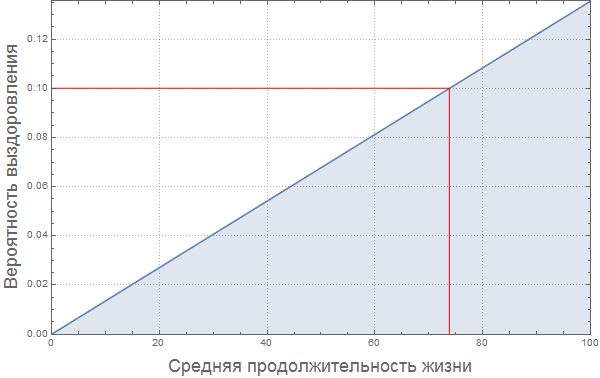
Как и в случае с вероятностью заражения, рассчитаем вероятности выздоровления для каждой из стран:
In[86]:=
![]()
Мы также можем визуализировать, что все это значит для всех стран. На рисунке ниже средние значения величин отмечены белой и зеленой линиями, а равное количество доли заболевших и вылечившихся отмечено черной пунктирной линией. Цвет фона показывает долю людей, которые пострадали от вируса во время вспышки, согласно информации, взятой из SIR-модели (см. начало статьи).
In[88]:=

Out[88]=
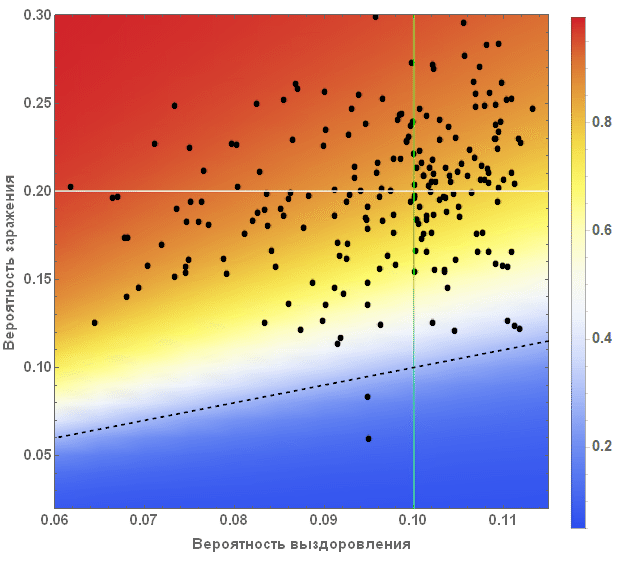
Виталий: Стандартный процесс моделирования включает в себя многократный запуск симуляции с целью лучше понять поведение системы, а также влияние на неё значений параметров. Принятые в нашем случае значения приведут к результату, который выглядит отвечающим здравой логике, как в случае, если бы мы столкнулись с тяжелой, но излечимой пандемией. Страны со слабой экономикой понесут больший ущерб, а с высокой — меньшие потери. Что здесь важно, так это то, по моему мнению, как этот контраст влияет на топологию миграций, демографию, и другие жизненные факторы. Также, следует ожидать, что сложные компоненты и нелинейность могут привести к неинтуитивным вариантам, нанося больший ущерб сильным и меньший — слабым.
Марко, могли бы вы подробнее рассказать о графике, полученном выше?
Марко: График описывает два главных параметра нашей модели: вероятность заражения и выздоровления. Каждая точка обозначает страну, если навести на нее курсор, то появится подпись с ее названием. Белые и зеленые линии обозначают средние значения параметров. Они разделяют диаграмму на четыре зоны. Верхний левый квадрат (большая вероятность заражения/маленькая вероятность выздоровления) — страны с наименее благоприятными условиями. Туда входят такие страны, как Сьерра-Леоне, Нигерия и Бангладеш. В нижнем правом квадрате находятся страны с наилучшими перспективами для подавления заболевания: США, Канада и Швеция. Черная пунктирная линия обозначает критическую черту: над ней находятся страны, в которых вероятность заражения больше вероятности выздоровления. В этих странах вспышка заражения очень вероятна. Ниже черты вероятность выздоровления больше вероятности заражения, и, соответственно, имеются шансы, что болезнь будет подавлена. Обратите внимание, что это только «основные параметры» модели и мы пока что ещё не рассмотрели влияние графа связей между странами. Также, обратите внимание, что страны ниже пунктирной линии могут остановить распространение заболевания. Если таких стран будет достаточно много, это, опять же, может уменьшить количество заражений.
Виталий: Как мы отмечали выше, наша симуляция рассматривает худшие варианты событий, чтобы можно было яснее увидеть различные эффекты пандемии. По этой причине мы сдвинули систему выше и большинство точек оказались над черной пунктирной линией. Читатели могут рассмотреть более реалистичные варианты параметров самостоятельно.
Марко: Чтобы отметить еще один недостаток наших первых моделей, предположим, что зараженные, выздоровевшие, и находящиеся под угрозой заражения передвигаются с разными скоростями. Тут есть еще один момент, на который нужно обратить внимание. Если мы установим значение коэффициента миграции/передвижения слишком высоким, то различия в регионах просто усреднятся! В реальности, процент путешествующих людей будет относительно низким в течении времени, рассматриваемого симуляцией, практически равным нулю. Чтоб увидеть распространение болезни, установим достаточно высокие значения скорости перемещения зараженных; будем игнорировать перемещения здоровых и выздоровевших. Это не критичное допущение, потому что они все равно никак не способствуют распространению вируса.
In[89]:=
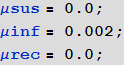
Очистим переменные, чтобы удостовериться, что мы начнём моделирование с «чистого листа».
In[92]:=
![]()
Как и раньше, инициализируем нашу модель полагая, что вначале во всех городах есть только восприимчивые к инфекции и нет зараженных или выздоровевших:
In[93]:=
![]()
Вспышка заболевания началась в Сьерра-Леоне (Гвинея), поэтому нужно найти, какая вершина графа отвечает этой стране:
In[95]:=
![]()
Out[95]=
![]()
Далее зададим в ней небольшую начальную долю зараженных людей:
In[96]:=
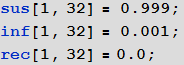
Затем, как и ранее, создаем рекуррентные соотношения, которые дадут нам решение:
In[99]:=

In[101]:=

Теперь можем запустить итеративный процесс:
In[103]:=
![]()
Out[103]=
![]()
Это первая проба, посмотрим, работает ли симуляция — изобразим временные зависимости долей выздоровевших, зараженных и восприимчивых для всех стран:
In[104]:=

Out[104]=
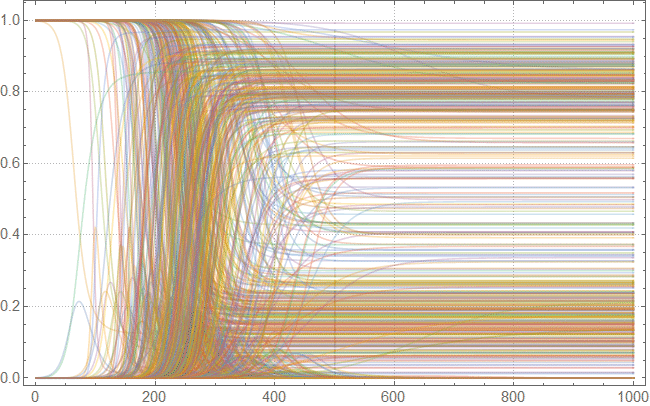
Обратите внимание, что по завершении симуляции, большинство линий обрели устойчивые значения. Это означает, что вспышка затихла. Вот сводка по общему количеству зараженных и умерших в течении всей вспышки:
In[105]:=
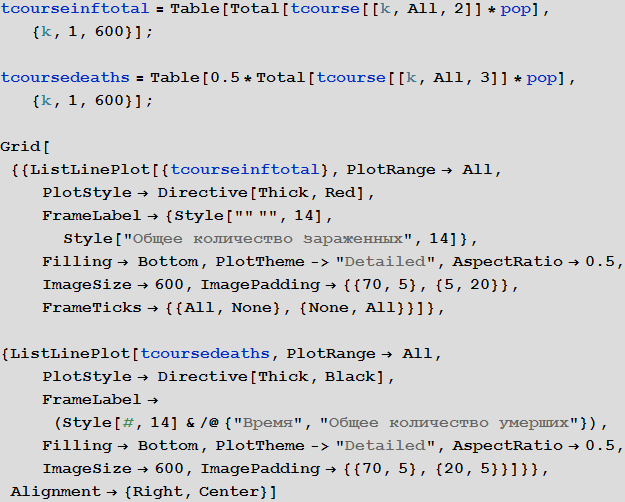
Out[107]=
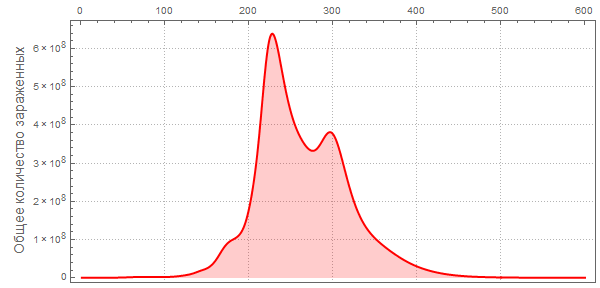
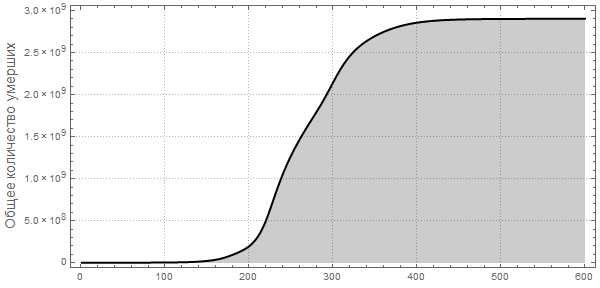
Теперь мы можем визуализировать глобальное распространение Эболы, посмотрев на ситуации в Мире в различные моменты времени. Число ниже показывает максимальную долю умерших людей среди всех стран.
In[108]:=
![]()
Out[108]=
![]()
In[109]:=
Out[109]//TableForm=
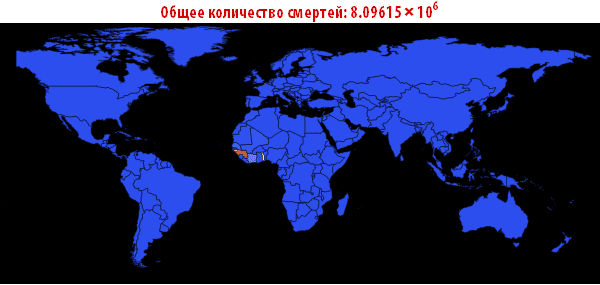
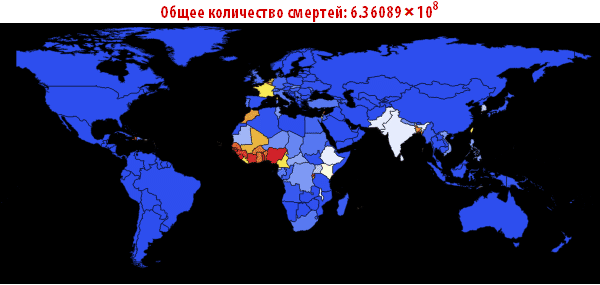
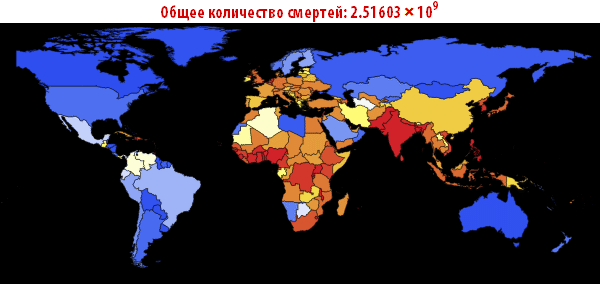
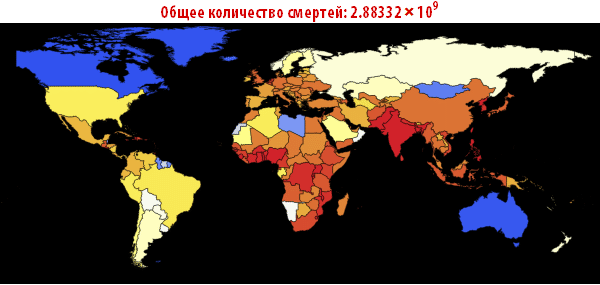
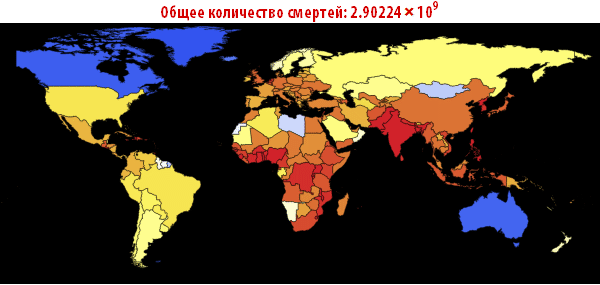
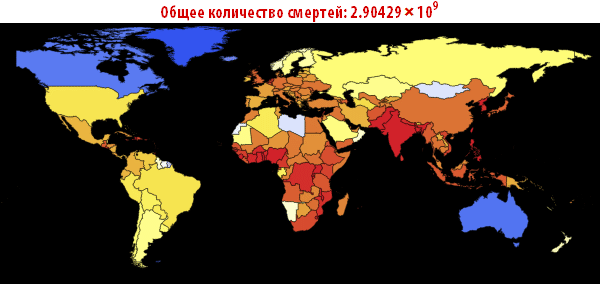
Обратите внимание, что количество умерших людей чрезвычайно высоко во всех наших симуляциях. Около трёх миллиардов погибших — такая вспышка может стать абсолютно разрушительной. Очень вероятно, что такая пандемия гораздо, гораздо крупнее, чем всё то, что мы наблюдали прежде. Причиной этого может быть выбор параметров; отношение вероятности заражения к вероятности выздоровления может быть другим. С другой стороны, мы моделировали вспышку заболевания, в которой системы относительно «инертны». Это означает, что они не принимают эффективных контрмер. Если бы мы смоделировали это, то потребовалось бы уменьшить вероятность заражения с течением времени, из-за действий правительств.
Сейчас это, разумеется, всего лишь концептуальная модель. Читатель может изменить определённые ее параметры, например, закрыть аэропорты и посмотреть, какой это окажет эффект. Он может изменить вероятности заражения и выздоровления и посмотреть, как это повлияет на результат. Тут есть множество параметров, с которыми можно поэкспериментировать (скажем, если отношение вероятности заражения к вероятности выздоровления будет очень велико, то такой сценарий потребует внимательного изучения, что может потребоваться, если вирус лихорадки Эбола мутирует и станет, к примеру, переноситься воздушно-капельным путем). Мы ещё (пока что) не подбирали параметры так, чтобы они оптимально описывали текущую вспышку заболевания.
Виталий: Я запускал модель много раз с разными значениями параметров. Например, если взять ситуацию, противоположную рассмотренной выше, задав вероятность выздоровления больше вероятности заражения, а начальное число зараженных очень малым:
In[110]:=

То мы получим гораздо меньшее число зараженных и больных:
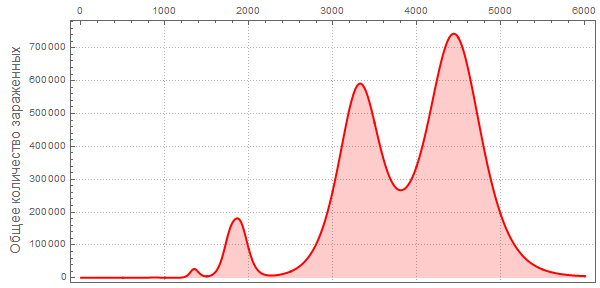
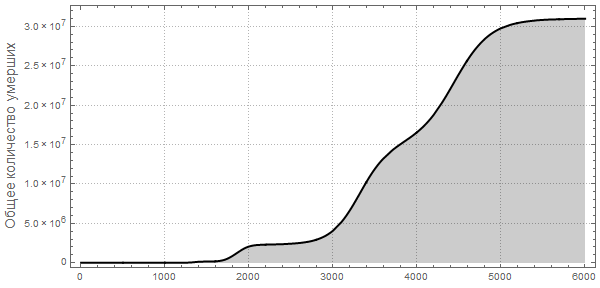
Также обратите внимание на другой характер максимумов, говорящий нам, что пандемии могут повторяться и с большей поражающей мощностью. Такие повторные вспышки описаны в The New York Times в разделе «Как соотносится текущая вспышка с предыдущими?» Также прогноз Центра по контролю и профилактике заболеваний США (CDC) и текущая стадия пандемии имеют практически экспоненциальный рост, совпадающий с самыми первыми (слева) пиками на графиках.
Можем ли мы откалибровать нашу модель с соответствии с реальными данными, например, по временной шкале или по абсолютному числу зараженных и выздоровевших?
Марко: Есть много статьей, в которых исследуется влияние, скажем так, плотности популяции на вероятности заражения, как например, упомянутая выше статья Hu и соавторов. Мы можем использовать эти работы или данные наблюдений для уточнения нашей собственной модели. Mathematica предлагает прекрасные инструменты для согласования параметрических кривых (или, моделей) с данным. Это поможет улучшить нашу модель. Относительно временной шкалы, мы должны подчеркнуть, что не вводили время на каждом шаге итерации. Тем не менее мы можем использовать данные наблюдений, например, для текущей вспышки и попытаться подобрать параметры ?, ?, и ?, так чтобы число смертельных случаев/случаев заражения и их изменение во времени правильно описывалось нашей моделью.
Виталий: Картина на графиках, полученных с помощью функций ListLinePlot и GeoRegionValuePlot, отличается от полученных с помощью упрощенной исходной модели, с которой мы начали. Теперь мы видим, что в ряде стран есть вспышка заболевания, а другие, похоже, устойчивы к ней. Для меня это выглядит более реалистичным. Можете ли вы прокомментировать это и, возможно, сравнить полученные результаты и результатами из статьи Дирка Брокманна (Dick Brockmann)?
Марко: Самый важный момент такой: высокие уровни миграции в первых моделях приводят к перемешиванию популяций и, в итоге, во всех популяциях соотношение количества людей из трех категорий становится одинаковым. Как и в статье Дирка Брокманна (Dirk Brockmann), мы видим, что транспортные потоки (граф) играют важную роль в распространении заболевания. Расстояние на графе очень важны. Это особенно важно, так как страны, где уровень выздоровевших превышает уровень инфицированных, по сути, остановили распространение заболевания.
Виталий: Марко, благодарю вас за впечатляющие сведения и потраченное время. У вас есть понимание, как в будущем можно улучшить модель или может быть вы хотите что-то сказать в заключении нашим читателям?
Марко: Довольно просто предложить еще идеи для улучшения модели: мы можем включить больше информации о передвижениях — улицы/машины, корабли, сети железных дорог и т. п. все это влияет на передвижение населения. Мы могли бы использовать данные сотовой связи или что-то подобное, чтобы лучше смоделировать актуальные перемещения людей. Также SIR-модель не учитывает инкубационный период, т. е. время до проявления первых симптомов заболевания. В нашей модели популяция описывается «ящиками»; число заразившихся и т. п. задается в процентном отношении. Это дает «хорошее» приближение, если число заболевших достаточно большое (также как задавать концентрации в абсолютных величинах имеет смысл, если молекул много), но в начале вспышки, когда зараженных мало, модели других типов, как например, многокомпонентная модель, могут быть более реалистичными. Представленная нами модель, может рассматриваться только как первый шаг; можно включать дополнительные факторы и изучать их значимость. Методом проб и ошибок мы можем попытаться описывать реальные вспышки все лучше и лучше. Но нам следует быть осторожными: чем больше факторов мы включим в модель, больше параметров мы получим. Это приведет к дополнительным проблемам, когда нам понадобиться оценивать параметры.
Мы могли заметить, что расчет не корректно отображает случаи в США и Европе. Сейчас нам известно о 18 людях, специально доставленных сюда. Они не являются частью естественного распространения заболевания. Также мы говорим о «процентах или некотором количестве процентов» популяции, мы не обсуждаем единичные случаи. С точки зрения эпидемиологии, в США или Испании сейчас не происходит ничего, относящегося к Эболе. Ситуация в Сьерра-Леоне и других африканских странах действительно больше подходит под нашу модель.
Наша модель не учитывает специфику эпидемии Эболы. Делается много допущений, и мы подбираем параметры так, чтобы распространение эпидемии было легко увидеть, но модель показывает только возможный порядок распространения: сначала страны Западной/Центральной Африки, потом Европа, и затем США. Это обоснованно и подтверждается другими гораздо более сложными моделями. Конечно, есть много других факторов, так распространение между соседними странами в Африке происходит не через авиаперелеты, а с помощью местного транспорта, люди пересекают границы пешком или на машинах. Наша модель, безусловно, только качественная и учитывает только один вид транспорта, а именно, авиаперелеты, что не описывает картину в целом, но показывает огромные различия между странами. В конечном итоге мы можем ожидать гораздо меньший процент летальных исходов в Европе и США, чем в странах Африки, с которых все началось. Модель показывает, что самая высокая вероятность распространения — между соседними африканскими странами, что и предсказывают другие бОльшие модели. Также отдельные страны Европы, как например Германия/Великобритания/Франция и т. п., больше, чем остальные, подвержены риску из-за авиасообщений. США, похоже, еще меньше подвержены риску, чем европейские страны, так что ощутимое число заболевших здесь появится позже. Все это качественно довольно верно. До Австралии и Гренландии заболевание дойдет нескоро или вообще никогда, что опять же согласуется с нашей модель (по крайней мере, если ρ~λ~1).
В этой связи я предположу, что выбор ρ=1 или меньше, чем λ больше соответствует действительности. Это в большей степени ограничит распространение на ряд африканских стран и на страны с низкими вероятностями заболевания в Европе и США. Хотя «среднемировая» вероятность заражения может быть ниже, чем вероятность выздоровления, по крайней мере в ряде стран из-за плотности населения и низкого качества здравоохранения локальное значение вероятности заражения может быть выше, чем вероятности выздоровления. Также число заразившихся будет очевидно меньше, чем предсказывает наша модель, так как мы не учитываем ассигнования правительств и Всемирной организации здравоохранения (WHO). Это легко смоделировать, уменьшая вероятность заражения с течением времени: больше в «богатых» странах, меньше в «бедных».
Прогноз должен рассматриваться с точки зрения вероятностей или рисков, что некоторые страны столкнутся с бОльшей естественной вспышкой, так как наша модель не учитывает индивидуальные случаи или случаи предумышленного перевоза пациентов в госпитали. Это означает, что вероятность заразиться лихорадкой Эбола для медсестры выше, чем для обычного гражданина, и конечно, мы это не учитываем. Также точное распространение эпидемии зависит от многих «случайных» факторов, которые невозможно разумным образом учесть в нашей или в других моделях. Можно ввести фактор случайности и прогнать модель достаточное число раз, чтобы сделать заключение о возможных сценариях или вероятностях. В этом смысле наша модель выступает качественно очень хорошо.
Качественная природа модели позволяет нам рассмотреть несколько сценариев: Что если отношение вероятности заражения и вероятности выздоровления изменится? Что если увеличится мобильность населения, т. е. изменится μ? Что если мы также учтем местный транспорт? Мы не пытались подобрать параметры/граф и т. д. для точного описания вспышки лихорадки Эбола; напротив, мы предлагаем базовую модель для описания разных сценариев и понимания основных параметров, входящих в модели такого типа.
Виталий: Я еще раз выражаю благодарность Марко и нашим читателям за участие в интервью.
Автор: OsipovRoman