После разделения Хабра на два ресурса получилось, думаю не только у меня, так, что статьи остались на Хабре, а в профиль на Гиктаймс перенесли только комментарии и рейтинг. При этом как пользователь без публикаций я не имею права голосовать за рейтинг автора понравившиеся статьи, что хотелось бы исправить. Идеи для статей если и были, то относились к тематике Хабра. Но комментарий в статье «Две недели спустя появления Geektimes: увы...» натолкнул на странную мысль — написать о математическом вязании. То есть о различных математических моделях, связанных крючком или спицами. Ну и немного о самих моделях тоже.
Странный аттрактор
Аттрактор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Одним из именных примеров аттрактора является аттрактор Лоренца.
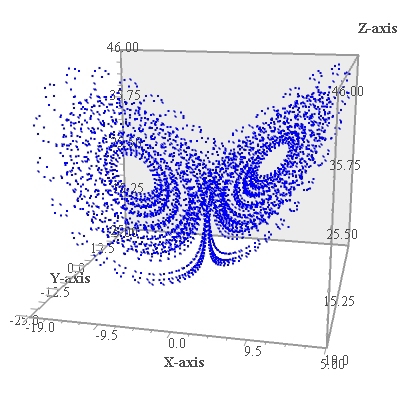
Аттрактор Лоренца был найден в численных экспериментах Лоренца, исследовавшего поведение траекторий нелинейной системы:
при значениях параметров: σ=10, r=28, b=8/3. Система возникает в следующих физических вопросах и моделях: конвекции в замкнутой петле, вращении водяного колеса, модели одномодового лазера, диссипативном гармоническом осцилляторе. Модель Лоренца является реальным физическим примером динамических систем с хаотическим поведением.
У математика Хинке Осинга вполне математическое хобби - вязание. Считая петли в свободное от работы время, она отдыхает. Как-то ее научный руководитель, профессор Краускопф неосмотрительно бросил: «Связала бы ты что-нибудь полезное!». И доктор Осинга связала.
Так появилась модель хаоса. Теперь единственный в мире вязаный хаос крутится под потолком в кабинете математиков в университете Бристоля.
Хинке Осинга, доктор математики, университет г.Бристоль: «Я вязала каждую свободную минуту. В основном по вечерам. Примерно по 2 часа в день на протяжении почти двух месяцев. В общей сложности, 85 часов. 25 с лишним тысяч петель, и получился хаос. Причем, весьма симпатичный». Теперь, когда его можно потрогать, математикам легче его изучать. Они занимаются этим уже 2 года (интервью 2004 года), моделируя на компьютере «уравнения Лоренца», которые как раз и описывают хаотические движения. Математики обещали бутылку шампанского тому, кто первым предложит другую связанную модель. Только через две недели пришли первые письма с фотографиями.
Гиперболическая плоскость
Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. В геометрии Лобачевского принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Псевдосфера (поверхность Бельтра́ми) — поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название подчёркивает сходство и различие со сферой, которая является примером поверхности с кривизной, также постоянной, но положительной. Название «псевдосфера» поверхности дал Бельтрами.
Он же обратил внимание на то, что псевдосфера реализует локальную модель геометрии Лобачевского.
Дайна Тайминя разрешила столетнюю проблему неевклидовой геометрии по визуализации гиперболических плоскостей. Гиперболические плоскости имеют отношение к неевклидовой геометрии, которую традиционно трудно визуализировать. Дайне Таймине удалось сделать это с использованием вязаных тканей. Свою первую модель гиперболической плоскости она связала крючком в 1997 году, чтобы использовать в студийном курсе неевклидовой геометрии. С тех пор она связала более сотни геометрических моделей.
Ее технику используют в экологии. Маргарет Вертхейм возглавляет проект по воссозданию обитателей кораллового рифа, используя технику кроше (вязания крючком), изобретённую математиком — прославляя удивительность кораллового рифа, и погружаясь в гиперболическую геометрию, которая лежит в основе создания коралла.
Видео на TED: Маргарет Вертхейм о красивой математике коралла (и вязания крючком), где дается простое объяснение евклидова и гиперболического пространства.
Бутылка Клейна
Бутылка Клейна — неориентируемая (односторонняя) поверхность, впервые описанная в 1882 году немецким математиком Ф.Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.
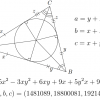
Поверхность Клейна в виде «фигуры 8», показанной на рисунке ниже, может быть представлена в виде системы уравнений с параметрами, которая выглядит гораздо проще, чем для классической бутылки Клейна:
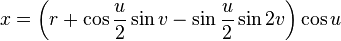
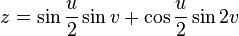
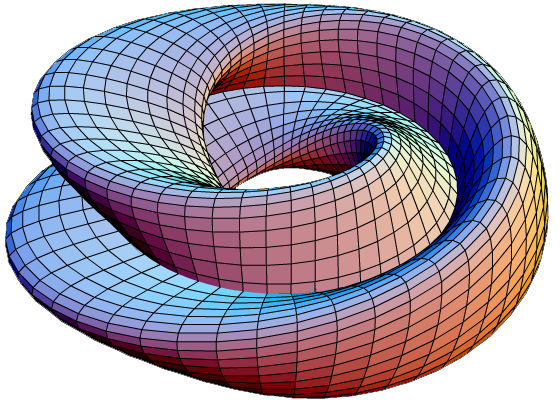
Если рассечь бутылку Клейна на две половинки вдоль плоскости симметрии, то получатся две зеркальных ленты Мебиуса, одна — с разворотом вполоборота вправо, другая — с разворотом вполоборота влево. Фактически, возможно рассечь бутылку Клейна так, что получится одна лента Мебиуса. Иначе, бутылка Клейна может быть представлена в виде двух лент Мебиуса, соединенных друг с другом обычной двухсторонней лентой. На рисунке ниже внутренняя поверхность этой ленты окрашена белым цветом, а внешняя — голубым.
Вязаная бутылка Клейна:
Как можно видеть, фирма Acme также делает стеклянные бутылки.
Фракталы
Фрактал (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения (любая часть фрактала подобна всему множеству целиком). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев.
Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского. Середины сторон равностороннего треугольника T0 соединяются отрезками. Получаются 4 новых треугольника. Из исходного треугольника удаляется внутренность срединного треугольника. Получается множество T1, состоящее из 3 оставшихся треугольников «первого ранга». Поступая точно так же с каждым из треугольников первого ранга, получим множество T2, состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность T0⊃T1⊃⋯⊃Tn⊃…, пересечение членов которой есть треугольник Серпинского.
Доктор Давид Уилстром хоть и мужчина, но тоже иногда вяжет. Вязанию его обучили на одном из текстильных семинаров, и с тех пор он в свободное время делает интересные вещи из ниток.
И, напоследок, еще несколько вязаных фракталов.
Дерево Пифагора
Эти пледы были созданы фирмой Woollythoughts. Они также делают необычные панно, изображение на которых видно только под определенным углом.
Множество Жюлиа
Источники:
Про вязаный аттрактор
Сайт Хинке Осинга и Бернда Краускопфа
Гиперболическое вязание
Дайна Тайминя
Гиперболическое вязание крючком
О выставке Дайны Таймини
Бутылка Клейна
Acme klein bottle company
Mathematical Knitting Network
Дерево Пифагора
Статья о математическом вязании, но изображения недоступны
Автор: urticazoku
