В этом посте я приведу несколько рисунков, нарисованных при помощи математических формул. Цель этих рисунков — не просто нарисовать что-то на экране (для этого есть компьютерная графика), а предложить простую формулу, определяющую рисунок.
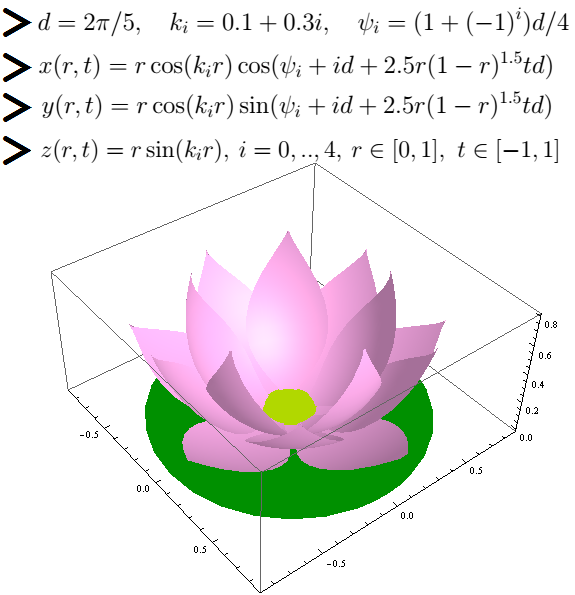
На первом рисунке изображён лотос. Рисунок построен в программе Wolfram Mathematica.
phi = 0;
dphi = 2*Pi/7;
theta[r_] := 0.4*r;
theta1[r_] := 1*r;
theta2[r_] := 0.7*r;
Show[
ParametricPlot3D[{r*Cos[phi], r*Sin[phi], 0}, {r, 0, 0.8}, {phi, 0,
2 Pi}, PlotStyle -> Darker[Green], Mesh -> None],
ParametricPlot3D[{r*Cos[phi], r*Sin[phi], 0.02}, {r, 0, 0.15}, {phi,
0, 2 Pi}, PlotStyle -> Yellow, Mesh -> None],
ParametricPlot3D[
Join[
Table[
{r*Cos[theta[r]]*Cos[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Cos[theta[r]]*Sin[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Sin[theta[r]]}, {i, 0, 6}],
Table[{r*Cos[theta1[r]]*Cos[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Cos[theta1[r]]*Sin[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Sin[theta1[r]]}, {i, 0, 6}],
Table[{r*Cos[theta2[r]]*
Cos[(dphi/2 + i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Cos[theta2[r]]*
Sin[(dphi/2 + i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Sin[theta2[r]]}, {i, 0, 6}]],
{r, 0, 1}, {t, -1, 1},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.3, 0], 20],
RGBColor[0.972, 0.658, 0.898],
Lighting -> {{"Directional",
Darker[White, 0.5], {2, 0, 2}}, {"Ambient", Darker[White]}}],
Mesh -> None],
PlotRange -> {{-0.85, 0.85}, {-0.85, 0.85}, {0, 0.8}}]
Эти формулы проще представить в сферической системе координат: длина радиус-вектора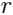 
, широта 
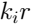, долгота 
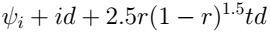. Здесь введён параметр 
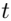. Смысл его заключается в том, что мы берём точку с долготой 
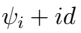и отступаем от неё на 
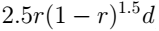в сторону уменьшения и увеличения долготы.
Следующий рисунок — симпатичный цветок. Формула задана в сферической системе координат, также сделано преобразование сжатия по оси z.
r[theta_, phi_] :=
If[(Pi/2 - Abs[theta] < Pi/8), 0.25*Sin[theta],
Sin[4*phi]*Cos[4*theta]];
Show[ParametricPlot3D[
{r[theta, phi]*Cos[theta]*Cos[phi],
r[theta, phi]*Cos[theta]*Sin[phi],
r[theta, phi]*Sin[theta]/Sqrt[3]},
{theta, -Pi/2, Pi/2}, {phi, 0, 2*Pi}, Mesh -> None,
PlotStyle -> Orange, PlotRange -> All, MaxRecursion -> 4],
SphericalPlot3D[0.16, theta, phi, Mesh -> None, PlotStyle -> Yellow]]
Вот ещё цветок.
xx[t_] := 0;
yy[t_] := -0.75 t*(1 - t);
zz[t_] := -3 t;
rr = 0.05;
x1[t_] := 0;
y1[t_] := -0.15 + 0.5 t;
z1[t_] := -1.6 + 0.5 t;
r[theta_, phi_] :=
If[(Pi/2 - Abs[theta] < Pi/8), 0.25*Sin[theta],
Sin[4*phi]*Cos[4*theta]];
Show[ParametricPlot3D[
{r[theta, phi]*Cos[theta]*Cos[phi],
r[theta, phi]*Cos[theta]*Sin[phi],
r[theta, phi]*Sin[theta]/Sqrt[3]},
{theta, -Pi/2, Pi/2}, {phi, 0, 2*Pi}, Mesh -> None,
PlotStyle -> Orange, PlotRange -> All, MaxRecursion -> 4],
SphericalPlot3D[0.16, theta, phi, Mesh -> None, PlotStyle -> Yellow],
ParametricPlot3D[{xx[t] + rr*Cos[phi], yy[t] + rr*Sin[phi], zz[t]},
{t, 0, 1}, {phi, 0, 2 Pi}, Mesh -> None, PlotStyle -> Green],
ParametricPlot3D[{x1[t] + phi*t*(1 - t), y1[t] - 0.5 phi*t*(1 - t)^3,
z1[t]},
{t, 0, 1}, {phi, -1, 1}, Mesh -> None, PlotStyle -> Green],
Boxed -> False, Axes -> None]
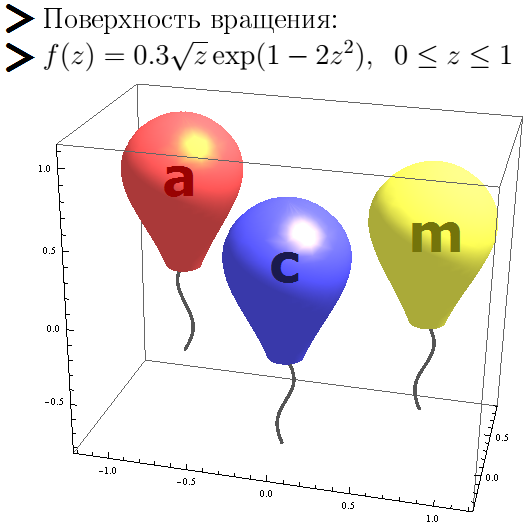
На этом рисунке изображены шарики, полученные как поверхность вращения для некоторой функции.
x1 = 0; y1 = 0; z1 = -0.2;
x2 = 0.8; y2 = 0.3; z2 = 0;
x3 = -0.8; y3 = 0.5; z3 = 0.1;
f[z_] := z*(1 - z);
f[z_] := 0.3 z^0.5*Exp[1 - 2 z^2];
gz[t_] := -0.6 t;
gy[t_] := 0.1 t*(1 - t);
gx[t_] := 0.05 Sin[6 t];
Show[ParametricPlot3D[{x1 + f[1 - z]*Cos[phi], y1 + f[1 - z]*Sin[phi],
z1 + z}, {z, 0, 1}, {phi, 0, 2*Pi},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.8, 0], 30], Lighter[Blue],
Lighting -> {{"Directional", White, {1.5, 0, 3}}, {"Ambient",
Darker[White]}}], Mesh -> None],
ParametricPlot3D[{x1 + gx[t], y1 + gy[t], z1 + gz[t]}, {t, 0, 1},
PlotStyle -> Directive[Thickness[0.0075], Lighter[Black]]],
ParametricPlot3D[{x2 + f[1 - z]*Cos[phi], y2 + f[1 - z]*Sin[phi],
z2 + z}, {z, 0, 1}, {phi, 0, 2*Pi},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.8, 0], 30], Lighter[Yellow],
Lighting -> {{"Directional", White, {1.5, 0, 3}}, {"Ambient",
Darker[White]}}], Mesh -> None],
ParametricPlot3D[{x3 + f[1 - z]*Cos[phi], y3 + f[1 - z]*Sin[phi],
z3 + z}, {z, 0, 1}, {phi, 0, 2*Pi},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.8, 0], 30], Lighter[Red],
Lighting -> {{"Directional", White, {1.5, 0, 3}}, {"Ambient",
Darker[White]}}], Mesh -> None],
ParametricPlot3D[{x2 + gx[1 - t], y2 + gy[1 - t],
z2 + gz[1 - t]}, {t, 0, 1},
PlotStyle -> Directive[Thickness[0.0075], Lighter[Black]]],
ParametricPlot3D[{x3 + gx[t], y3 + gy[1 - t], z3 + gz[1 - t]}, {t, 0,
1}, PlotStyle -> Directive[Thickness[0.0075], Lighter[Black]]],
PlotRange -> All]
Рисунок напоминает о командном чемпионате мира по программированию ACM, четвертьфиналы которого проходит осенью. (На финале этого чемпионата за правильно решённую задачу команде дают шарик.)
Теперь приведу несколько праздничных рисунков.
Вот рисунок, сделанный на Новый год. Это ёлочка, построенная с помощью отрезков.
a = 1;
b = 0.5;
c = 1.5;
h = 3.5;
dr[k_] := b + (c - b)/n*k;
dz[k_] := -(a - a/n*k);
z[k_] := h - h*k/n;
cnt = 0;
Do[Do[cnt = cnt + 1; phi = j*2*Pi/m + i*2*Pi/n;
ldx[cnt] = dr[i]*Cos[phi]; ldy[cnt] = dr[i]*Sin[phi];
ldz[cnt] = dz[i]; lz[cnt] = z[i], {j, 1, m}], {i, 1, n}]
ParametricPlot3D[
Table[{ldx[i]*t, ldy[i]*t, lz[i] + ldz[i]*t}, {i, 1, cnt}], {t, 0,
1}, PlotStyle -> Directive[Darker[Green], Thickness[0.005]]
Это звезда, сделанная на 23 февраля.
gamma = Pi/10;
rho = 1;
p = rho*Sin[gamma];
k[phi_] := Floor[(phi + 0.2*Pi)/(0.4*Pi)];
s[phi_] := Sign[phi - 0.4*k[phi]*Pi];
alpha[phi_] := s[phi]*(Pi/2 - gamma) + 0.4*k[phi]*Pi;
PolarPlot[p/Cos[phi - Pi/2 - alpha[phi - Pi/2]], {phi, 0, 2*Pi},
PlotStyle -> Directive[Red, Thickness[0.01]]]
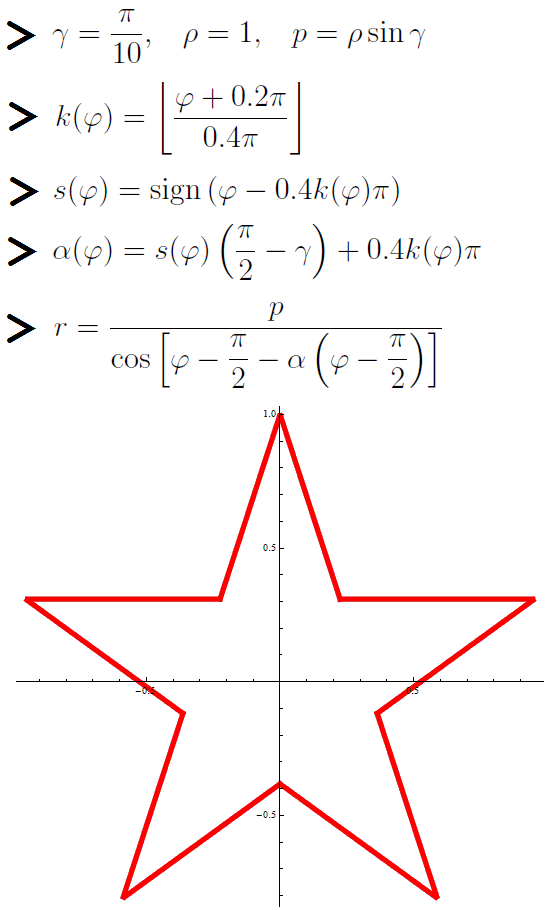
Звёздочка задана при помощи полярного уравнения прямой.
Кстати, параметр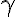 
(половина угла луча звезды) можно варьировать. Данная звезда соответствует значению 
.
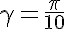При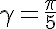 
получаем звездочку, похожую на морскую звезду:
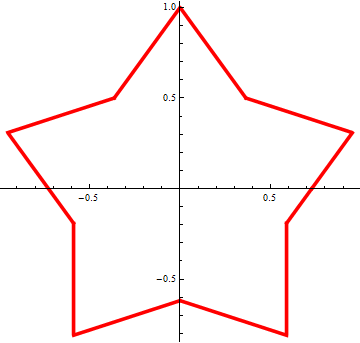
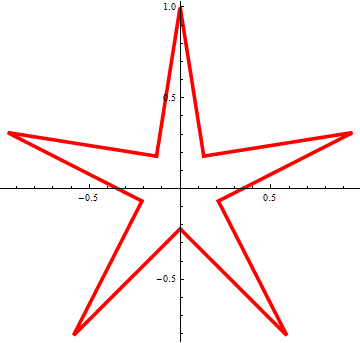
При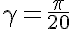 
получаем остроконечную звезду:
Вот картинка, которая подходит ко Дню Святого Валентина.
f[x_, y_] := x^2 + (y - (x^2)^(1/3))^2 - 1;
h1[x_] := (x^2)^(1/3) + Sqrt[1 - x^2];
h2[x_] := (x^2)^(1/3) - Sqrt[1 - x^2];
Do[x0[i] = 1 - (i - 1)/6; y0[i] = h1[x0[i]]; k[i] = 4 + i, {i, 1, 6}];
x0[7] = 0; y0[7] = h1[x0[7]]; k[7] = 7;
xx0[1] = 0.95; yy0[1] = h2[xx0[1]];
kk[1] = 6; Do[xx0[i] = 1.1 - 0.15*i; yy0[i] = h2[xx0[i]];
kk[i] = 4 + i, {i, 2, 6}]
xx0[7] = 0; yy0[7] = h2[xx0[7]]; kk[7] = 6;
RegionPlot[
Or @@ Table[(f[(x - x0[i])*k[i], (y - y0[i])*k[i]] <=
0) || (f[(x + x0[i])*k[i], (y - y0[i])*k[i]] <= 0), {i, 1,
7}] ||
Or @@ Table[(f[(x - xx0[i])*kk[i], (y - yy0[i])*kk[i]] <=
0) || (f[(x + xx0[i])*kk[i], (y - yy0[i])*kk[i]] <= 0), {i, 1,
7}],
{x, -1.5, 1.5}, {y, -2.5, 2.5}, PlotStyle -> Red, AspectRatio -> 0.9,
PlotRange -> All, MaxRecursion -> 5]
Можно даже сделать математическое признание:
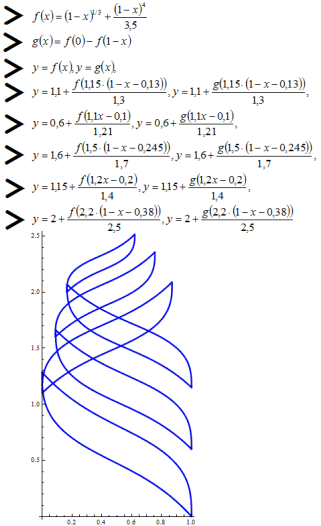
А вот ещё одно математическое сердечко. Рассматривается автономная система из 2-х дифференциальных уравнений 1-го порядка. Построен фазовый портрет этой системы (нарисованы траектории системы при различных начальных условиях) и найден общий интеграл системы.
Эта система может быть получена при дифференцировании общего интеграла по t. Таким способом (решая систему дифференциальных уравнений) можно строить графики уравнений.
А это математическая открытка к 8 Марта. На рисунке изображён некий абстрактный компьютер, который построил график лемнискаты Бернулли.
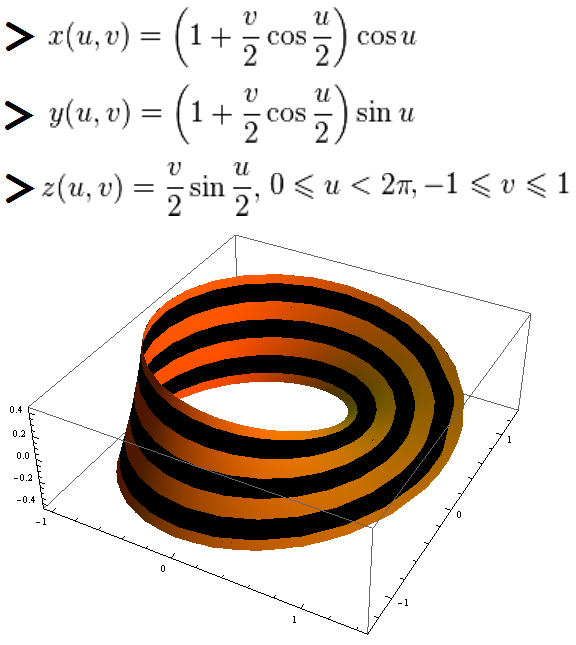
На рисунке изображена георгиевская лента Мёбиуса к 9 Мая.
f[i_, u_] :=
If[i == 0, -1 + 1/7 + u/7,
If[i == 6, -1 + 2*i/7 + u/7, -1 + 2*i/7 + u*2/7]];
ParametricPlot3D[
Evaluate@Table[{(1 + f[i, u]/2*Cos[phi/2])*
Cos[phi], (1 + f[i, u]/2*Cos[phi/2])*Sin[phi],
f[i, u]/2*Sin[phi/2]}, {i, 0, 6}], {u, 0, 1}, {phi, 0, 2*Pi},
Mesh -> None,
PlotStyle -> {Orange, Black, Orange, Black, Orange, Black, Orange}]
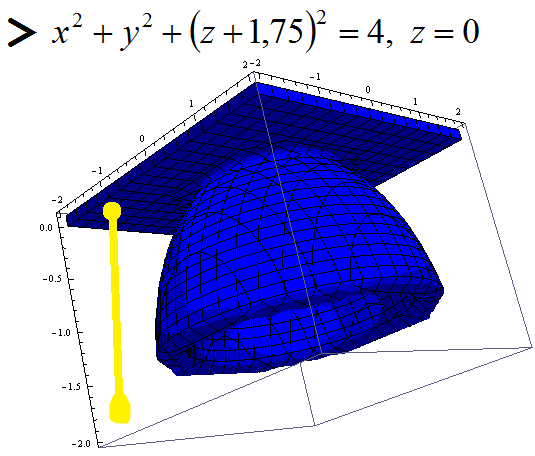
На следующем рисунке изображена квадратная академическая шапочка, рисунок подходит для 1 сентября.
RegionPlot3D[((x^2 + y^2 + (z + 1.75)^2 <= 4 &&
x^2 + y^2 + (z + 1.75)^2 >= 4 - 1.4) || (z <= 0.1 &&
z >= 0)) && (z >= -1.5), {x, -2, 2}, {y, -2, 2}, {z, -2, 0.1},
BoxRatios -> {1, 1, 0.8}, PlotStyle -> Blue]
На этом рисунке изображён логотип ДВФУ:
Вот сам логотип:
А это трёхмерный логотип ДВФУ, который также построен по математическим формулам в пакете Wolfram Mathematica.
g[z_] := 1/(1 + (1 - z)^2) - 1/2;
h[z_] := 1 - 1/2*Sqrt[1 + (z*Sqrt[3])^2];
f[z_] := If[z >= 0 && z <= 1, g[z], If[z >= 1 && z <= 2, h[z - 1]]]
phit[t_] := 2*Pi*t;
zt[t_] := 1.4*t;
zt1[t_] := 0.3 + 1.4*t;
zt2[t_] := 0.6 + 1.4*t;
phit1[t_] := 2*Pi*t;
phit2[t_] := 2*Pi*t;
k = 0.111;
ParametricPlot3D[{{f[zt[t] + k*s]*Cos[phit[t]],
f[zt[t] + k*s]*Sin[phit[t]],
zt[t] + k*s}, {f[zt1[t] + k*s]*Cos[phit1[t]],
f[zt1[t] + k*s]*Sin[phit1[t]],
zt1[t] + k*s}, {f[zt2[t] + k*s]*Cos[phit2[t]],
f[zt2[t] + k*s]*Sin[phit2[t]], zt2[t] + k*s}}, {t, 0, 1}, {s, -1,
1}, PlotStyle -> Blue, Mesh -> None, Axes -> False, Boxed -> False]
Автор: grenkin
