
Расскажу о различных реализациях эффекта размытия на GLSL.
Для начала хочу сразу предупредить — я поставил для себя ограничения использовать версию GLSL не выше 1.1. Это нужно для того, чтобы приложение работало на как можно большем количестве устройств и систем. Так, например, у меня были в распоряжении iMac с Radeon HD 6750M и максимально поддерживаемой версией GLSL 1.2, ноутбук с Kubuntu на intel hd 4000 с версией GLSL 1.3 и десктоп с GeForce gtx560.
Эффекты постараюсь описать простыми словами и без сложных формул, основная цель — привести примеры способов размытия. Статья является подготовительной к последующим двум статьям.
Размытие по Гауссу
Рассмотрим классическое гауссово размытие. Где только о нем не писалось, возможно это самый популярный способ размытия в геймдеве и не только. Но я не могу его не рассмотреть, хотя бы вкратце.
Что вообще представляет из себя размытие? Грубо говоря это усреднение соседних пикселей, то есть рассматривая текущий пиксель, мы находим средний цвет всех его соседей в определенном радиусе. Но если использовать простое среднее арифметическое (равномерное распределение), то размытие будет не очень красивым. Поэтому обычно соседей умножают на коэффициенты, значения которых подчиняются нормальному закону распределения (оно же распределение Гаусса, отсюда и название размытия).


размытие с равномерным и нормальным распределением соответственно
У Гауссова размытия есть одно важное свойство — сепарабельность. Это дает возможность разделить алгоритм на две части — размытие по координате x и размытие по y. Таким образом коэффициенты не нужно рассчитывать для всех соседей, достаточно найти для одного столбца или строки. Коэффициенты можно найти по формуле Гаусса:
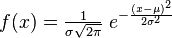 ,
,
где μ — математическое ожидание, а σ — дисперсия.
Реализация такого размытия довольно проста, нам понадобятся два буфера одинакового формата и предрассчитанный массив коэффициентов размытия:
- Рендерим сцену в первый буффер
- Рендерим изображение во второй буффер с шейдером размытия по вертикали
- Рендерим снова в первый буффер с размытием по горизонтали
#version 110
attribute vec2 vertex;
attribute vec2 texCoord;
varying vec2 vTexCoord;
void main() {
gl_Position = vec4(vertex, 0.0, 1.0);
vTexCoord = texCoord;
}
Фрагментный:
#version 110
const int MAX_KOEFF_SIZE = 32; //максимальный размер ядра (массива коэффициентов)
uniform sampler2D texture; //размываемая текстура
uniform int kSize; //размер ядра
uniform float koeff[MAX_KOEFF_SIZE]; //коэффициенты
uniform vec2 direction; //направление размытия с учетом радиуса размытия и aspect ratio, например (0.003, 0.0) - горизонтальное и (0.0, 0.002) - вертикальное
varying vec2 vTexCoord; //текстурные координаты текущего фрагмента
void main() {
vec4 sum = vec4(0.0); //результирующий цвет
vec2 startDir = -0.5*direction*float(kSize-1); //вычисляем начальную точку размытия
for (int i=0; i<kSize; i++) //проходимся по всем коэффициентам
sum += texture2D(texture, vTexCoord + startDir + direction*float(i)) * koeff[i]; //суммируем выборки
gl_FragColor = sum;
}
Эффект боке
На самом деле это основная причина написания статьи — я хотел рассказать как довольно легко получить данный эффект. Алгоритм похож на предыдущий, но есть различия:
- Нормальный закон распределения можно заменить на равномерный
- Добавляется еще один, третий проход
- Размытие теперь происходит не по вертикали и горизонтали, а по трем векторам, угол между которыми 120°
- В шейдере теперь помимо суммы цвета, находится так же максимальный цвет по всем выборкам, после чего оба цвета смешиваются в заданной пропорции
#version 110
uniform sampler2D texture; //размываемая текстура
uniform vec2 direction; //направление размытия, всего их три: (0, 1), (0.866/aspect, 0.5), (0.866/aspect, -0.5), все три направления необходимо умножить на желаемый радиус размытия
uniform float samples; //количество выборок, float - потому что операции над этим параметром вещественные
uniform float bokeh; //сила эффекта боке [0..1]
varying vec2 vTexCoord; //входные текстурные координаты фрагмента
void main() {
vec4 sum = vec4(0.0); //результирующий цвет
vec4 msum = vec4(0.0); //максимальное значение цвета выборок
float delta = 1.0/samples; //порция цвета в одной выборке
float di = 1.0/(samples-1.0); //вычисляем инкремент
for (float i=-0.5; i<0.501; i+=di) {
vec4 color = texture2D(texture, vTexCoord + direction * i); //делаем выборку в заданном направлении
sum += color * delta; //суммируем цвет
msum = max(color, msum); //вычисляем максимальное значение цвета
}
gl_FragColor = mix(sum, msum, bokeh); //смешиваем результирующий цвет с максимальным в заданной пропорции
}

размытие с разным коэффициентом bokeh: 0.2, 0.5, 0.8 (картинка кликабельна)
Экспериментально я выяснил, что наилучший коэффициент смешивания, обеспечивающий более-менее красивый эффект приближенный к реальному — это 0.5.
Недостатки этого метода:
- На один draw call больше и примерно на треть больше выборок по сравнению с предыдущим методом
- Форма боке — только правильные многоугольники с четным количеством углов
- Невозможно применить в алгоритме размытия по глубине
Есть еще несколько способов сделать этот эффект, вот один из них: проходимся по текстуре специальным шейдером, в котором выявляем наиболее контрастные места и записываем их координаты в буффер, далее размываем текстуру любым способом без эффекта боке, после чего рендерем прямо поверх нее спрайты-боке в тех координатах, что нашли на первом шаге. Достоинства такого метода — форма боке может быть любой формы, из недостатков — нужны геометрические шейдеры, что исключает слабые девайсы, а так же на каждый пиксель боке не отрисуешь — получим дикий филлрейт.
Размытие по глубине
Полное название эффекта — глубина резко изображаемого пространства, или DoF (Depth Of Field). Название говорит само за себя — все, что находится в фокусе — четко, вне фокуса — размыто. На первый взгляд эффект кажется простым, но есть моменты, которые его усложняют как в плане стоимости ресурсов, так и в плане реализации. Один из его недостатков — невозможно применить предыдущие подходы, из-за того, что он не обладает свойством сепарабельности, а значит нельзя разделить на несколько проходов (размытие по вертикали и горизонтали). Иногда можно смухлевать: отрендерить сначала задний план и размыть его, потом передний без размытия. Конечно это будет не полноценный эффект, но ощущение размытия по глубине будет. Но если сцена заполнена объектами по всей глубине, то придется размывать более «честным» способом. Но совсем честные способы обычно не используют — слишком много выборок, поэтому как правило в качестве выборок берут небольшое облако точек в определенном радиусе от рассматриваемой. Наиболее оптимальное распределение таких точек носит название диск Пуассона — от полностью случайного распределения точек его отличает то, что точки находятся примерно на равном расстоянии друг от друга. Есть множество способов получить диск Пуассона, я для себя использую этот:
- пусть r — радиус диска, тогда верхняя граница диска yMax=r, а нижняя yMin=-r.
- в цикле по yR от yMin до yMax выполним следующее:
- найдем xMax=cos(asin(yR/r))*r и xMin=-xMax.
- во вложенном цикле по xR от xMin до xMax найдем точку с координатами (xR, yR).
- далее координаты этой точки сместим на случайную величину от -r/4 до r/4
- полученные таким образом точки и есть искомые.
Что из себя представляет этот алгоритм? Мы просто грубо говоря делим окружность сеткой и идем построчно по узлам этой сетки слева направо сверху вниз. Координаты этих узлов случайным образом немного смещаем и получаем искомый диск Пуассона.
На самом деле это не совсем диск Пуассона, но он очень на него похож, сравните сами (слева моя реализация, справа точки сгенерированные по этому алгоритму):
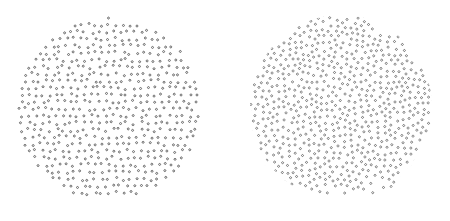
float yMax = r;
float yMin = -r;
yMin += fmod(yMax-yMin, 1)/2;
for (float y=yMin; y<yMax; y++) {
float xMax = cos(asin(y/r))*r;
float xMin = -xMax;
xMin += fmod(xMax-xMin, 1)/2;
for (float x=xMin; x<xMax; x++)
points.append(QPoint(x+floatRand(-r/4, r/4), y+floatRand(-r/4, r/4)));
}
На картинках выше точек очень много, на деле их достаточно около 10-20. После того как точки получены, по ним можно делать выборку. Но сначала поговорим о силе размытия.
Информацию о силе размытия для каждого пикселя будем хранить в альфа-канале. Сила размытия варьируется от -1 до 1, где единица — максимальное размытие, ноль — размытия нет. Я использовал HDR текстуру (RGBA16F), но эту информацию можно закодировать и в обыкновенный 8-битный альфа-канал:
a=depth*0.5+0.5 — кодирование
a=depth*2.0-1.0 — декодирование, где depth — сила размытия [-1..1]
Параметр depth (сила размытия) можно рассчитать по формуле: (focalDistance+zPos)/focalRange, где focalDistance фокусное расстояние, focalRange — диапазон или глубина размытия. Отрицательность значения depth говорит том, что текущий объект или фрагмент находится перед фокусом, если depth положительное — то за фокусом. Кстати, на самом деле не обязательно хранить знак, это увеличит диапазон значений в два раза (может быть критично для 8-битной текстуры), но при этом в шейдере при размытии невозможно будет понять, перед или за фокусом находится фрагмент — из-за этого могут возникнуть артефакты.
Итак, делая выборку используя диск Пуассона мы получаем информацию о цвете пикселя и о том с какой силой его нужно размывать. Помните коэффициенты выборок в двух предыдущих алгоритмах? Так вот, теперь в роли этих коэффициентов выступает сила размытия (конечно по модулю). Так же сила размытия влияет на радиус размытия текущего фрагмента. Еще следует рассказать о паразитном эффекте возникающем при текущей реализации — если граница глубины резкая (переход между дальним и ближним объектом), то между ними может наблюдаться нечто вроде муара или ореола, в этом случае просто корректируем коэффициент.
В качестве дополнительного улучшения алгоритма можно использовать вторую текстуру — меньшего размера и слегка размытую. Это позволит сократить количество выборок и улучшить качество размытия.
float blur = clamp((focalDistance+zPos)/focalRange, -1.0, 1.0);
gl_FragColor = vec4(color, blur);Вершинный шейдер размытия такой же как и в предыдущих методах, фрагментный:
#version 110
const int MAX_OFFSET_SIZE = 128; //максимальный размер массива точек диска Пуассона
uniform sampler2D texture; // текстура с отрендеренной сценой
uniform sampler2D lowTexture; // уменьшенная и размытая текстура со сценой
uniform int offsetSize; // размер массива точек диска Пуассона
uniform vec2 offsets[MAX_OFFSET_SIZE]; // диск Пуассона
varying vec2 vTexCoord; // входящие текстурные координаты
void main() {
float currentSize = texture2D(texture, vTexCoord).a; //запоминаем силу размытия фрагмента
vec4 resulColor = vec4 (0.0); //результирующий цвет
for (int i=0; i<offsetSize; i++) {
vec4 highSample = texture2D(texture, vTexCoord+offsets[i]*currentSize); //делаем выборку
vec4 lowSample = texture2D(lowTexture, vTexCoord+offsets[i]*currentSize);
float sampleSize = abs(highSample.a);//вычисляем силу размытия выбранной точки
highSample.rgb = mix(highSample.rgb, lowSample.rgb, sampleSize); //смешиваем цвет размытой и оригинальной текстуры исходя из силы размытия
highSample.a = highSample.a >= currentSize ? 1.0 : highSample.a; //корректировка весов (вклад, окторый вносит текущая выборка в результирующий цвет)
sampleSize = abs(highSample.a);
resultColor.rgb += highSample.rgb * sampleSize; //суммируем цвет
resultColor.a += sampleSize; //увеличиваем общий вес
}
gl_FragColor = resultColor/resultColor.a;
}

результат работы шейдера — размытая палка
Ссылки
- encelo.netsons.org/2008/04/15/depth-of-field-reloaded/ — один из способов сделать DoF
- www.gamedev.net/topic/563149-real-time-bokeh-high-quality-dof/ — я понял, что изобрел очередной велосипед, после того как наткнулся на эту страницу и прочитал последний пост
- steps3d.narod.ru/tutorials/depth-of-field-tutorial.html — реализация Dof
- www.jasondavies.com/poisson-disc/ — как сгенерировать диск Пуассона
- openglinsights.com/ — в этой книге рассматривается реализация DoF с эффектом боке на GLSL 4.2
Автор: Torvald3d






