Примем сокращения: натуральный ряд чисел (НРЧ); задача факторизации больших чисел (ЗФБЧ).
Манипулирование с натуральными числами возможно как непосредственно со значениями, так и с характеристиками – свойствами чисел. Удобство такого манипулирования во многом определяется моделью числа. Желательно разнообразие моделей иметь ограниченным, а структурное построение простым. Описания свойств моделей натуральных чисел (впрочем, и любых других чисел) желательно иметь в количественном выражении, в формализованном виде. Зависимость значений показателей свойств от разрядности чисел необходимо устранить, либо выбирать свойства свободные от таких зависимостей. Любая классификация в своей основе имеет свойства – это элемент формализации. Основной вопрос в работе – факторизация чисел – в связи с чем ниже сформулируем вариант теоремы факторизации натурального числа.
В теореме говорится о том, что трудности факторизации возникают не для всех чисел, следовательно, сложной процедуре факторизации необходимо подвергать не все числа НРЧ, а только их некоторую (меньшую) часть. В тексте теоремы не говорится, как эту меньшую часть формализовать и сделать удобной для последующей обработки. Но в работе как раз и пойдет речь о формировании удобного для обработки представления чисел такого меньшего множества.
Теорема факторизации натуральных чисел
Произвольное составное натуральное число N путём последовательного выполнения над ним некоторых элементарных преобразований может быть представлено произведением вида
N =2t2∙3t3∙5t5∙(pk+30∙t), где 0 ≤ ti, i = 2,3,5, t – натуральное, рk > 5 – простое.
Теорема
1. Если N – составное чётное натуральное число, то оно представимо в виде N=2t2∙n2,
где n2 ≡ 1(mod 2) – составное нечётное число, t2=1(1)…, и 2 ∤ n2;
2. Если N = n2 – составное нечётное число, оканчивающееся цифрой 5, то оно представимо в виде N=5t5∙n5, где n5 – составное нечётное число, t5 = 1(1)…; и 5 ∤ n5;
3. Если N = n5 — составное нечётное число, не оканчивающееся цифрой 5, а его свёртка s(N) (сумма цифр) кратна числу 3, то оно представимо в виде N=3t3∙n3, где n3 – составное нечётное число,
t3 = 1(1)…; и 3 ∤ n3;
4. Если N = n3 — составное нечётное число, с последней цифрой (флексией) ф ϵ {1, 3, 7, 9}, то оно имеет вид N=(pk+30∙t), где t = 1(1)… – натуральное число, а pk ϵ {7,11,13,17,19,23,29,31}, и факторизацию можно выполнить, например, используя понятие предельного контура и ф-инварианта нечетного числа или одним из существующих известных методов.
Вместо доказательства. Далее текст работы, включая таблицу 3, является по существу доказательством первой части теоремы (о представлении числа в виде модели N = 30∙t + pk). По ходу изложения возникают полные и усеченные модели НРЧ, плоские и объемные. Множество всех натуральных чисел разделяется на два подмножества. Первое – интуитивно воспринимаемое как большее содержит натуральные числа, которые факторизуются элементарными средствами (используются простейшие признаки делимости на простые числа 2, 3, 5). Второе подмножество – меньшее, которое содержит и все нечетные простые (кроме 3 и 5), и факторизация которых представляет особенно для больших чисел непреодолимую проблему настоящего времени. Последнее известное по публикациям факторизованное число описывается 232 десятичными цифрами.
Известная аналитическая модель НРЧ в виде перечня 30k, 30k ± 1, 30k ± 3,…, 30k ± 15,
k = 1(1)∞, соотношений позволяет понять, как можно описать те из чисел, которые должны содержаться в каждом из указанных подмножеств, т. е. по существу выполнить такое разбиение НРЧ.
Мультипликативное представление числа 30 имеет вид 30 = 2∙3∙5. Натуральные числа N, сравнимые с нулем по модулю делителей числа 30, N ≡ 0 (mod2), N ≡ 0 (mod3), N ≡ 0 (mod5) – это все четные числа, числа, делящиеся на три без остатка, и нечетные числа, оканчивающиеся цифрой 5.
Оказывается, множество натуральных чисел с нарушением подобных свойств распадается на классы эквивалентности с другими простыми, хорошо различимыми признаками. Таким образом, задача в работе состоит в разделении НРЧ на два подмножества, и получении описания меньшего в простой и удобной для дальнейшей обработки чисел форме.
Классы натуральных чисел. Положим в основу рассматриваемой классификации два очень просто определяемых показателя свойств (s, ф) чисел. Первый показатель обозначен символом s,
1 ≤ s ≤ 9, назван сверткой (это сумма цифр числа, доведенная до одной цифры) числа, он характеризует свойство делимости числа на три, а второй показатель обозначен символом ф,
0 ≤ ф ≤ 9, – назван флексией (окончанием, последней цифрой) числа, характеризует свойство конечного числа иметь последнюю цифру.
Пример 1. N = 4757, s(N) = ((4 + 7 + 5 + 7 = 23) → (2 + 3)) = 5; ф(N) ≡ N(mod10) = 7.
Пара свойств чисел, характеризуемых показателями (s, ф), разбивает НРЧ на не пересекающиеся классы (эквивалентности), которые имеют одинаковые значения пары показателей. Характеристикой класса чисел, которому принадлежит число N = 4757, является пара со значением (s, ф) = (5, 7).
Количество Т(s, ф) классов чисел, различимых по такой характеристике, определяется произведением диапазонов изменения значений каждого показателя двух свойств числа
Т(S, Ф) = S×Ф = 9×10 = 90.
Объем каждого класса включает бесконечное множество натуральных чисел, среди которых есть наименьшее число в классе. Поместим наименьших представителей всех классов в левую часть таблицы 1, а справа ее продолжим, заполняя (по образцу слева) клетки таблиц подряд следующими натуральными числами.
Таблица 1 – Классы Т(s, ф) чисел с периодом 90. Плоская модель НРЧ
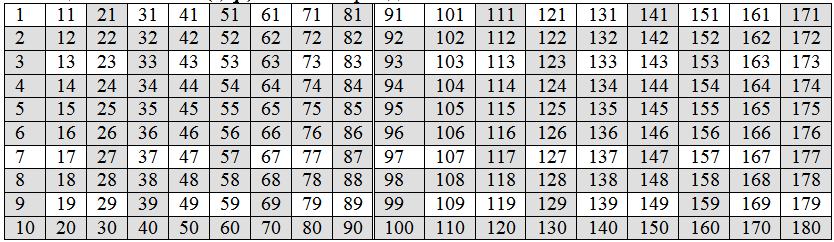
Анализ содержимого таблицы ( множество чисел Т-90) показывает, что в левой части таблицы 10×9 все числа наименьшие в своем классе и имеют разные значения характеристики (s, ф). Правая часть таблицы 10×9 аналогично левой части заполнена представителями разных классов с такой же характеристикой (s, ф), но с очередным увеличенным на 90 единиц значением (периодом) элемента. Подобные таблицы можно продолжить до бесконечности и сдвигать их влево с наложением на 1-ю (левую) таблицу. В итоге получим трехмерный параллелепипед, в котором над каждой клеткой нижней таблицы выписаны все числа, образующие класс натуральных чисел с фиксированным значением пары (s, ф).
Объемная модель НРЧ
По существу нами получена еще одна уже объемная модель НРЧ. Ее преимущества проявляются в возможности существенно урезать НРЧ без потери важных позиций, например, позиций, содержащих простые числа. Покажем, как это можно сделать.
Во-первых, вычеркнем строки таблицы 1, содержащие четные числа и нечетные, оканчивающиеся пятеркой, во-вторых, удалим классы чисел, кратные тройке. Клетки таблицы таких классов принадлежат диагоналям параллельным побочной диагонали таблицы. В таблице 1 удаляемые ячейки (классы) выделены заливкой.
Сохранились не закрашенные клетки-классы Т(s, ф), число которых 24 (оставшиеся после вычеркивания числа назовем множеством Т-24), им соответствуют ячейки таблицы без заливки. Возможными флексиями в оставшихся классах будут только ф = 1,3,7,9 и с каждой флексией по 6 значений свертки, т. е. 24 класса. Вполне очевидно, что простые числа могут появляться в пределах только этих классов. Действительно, в левой таблице из 24 наименьших представителей всех классов 22 являются простыми числами. Лишь две ячейки (из 24) заполнены составными числами 7×7 = 49 и 7×11 = 77, полученными умножением наименьшего остающегося простого числа 7 на себя и на следующее за ним простое число 11.
Алгебраическая группа вычетов генераторов классов
Будем продолжать реформирование НРЧ, вернемся к числу 30 = 2∙3∙5. Вспомним, что восьмерка простых чисел р(i) = {7,11,13,17,19,23,29,31} образует мультипликативную группу Э (группу Эйлера) вычетов восьмого порядка по этому модулю. Единичный элемент отождествляется с простым числом 31, р(i) ≡ 31(mod30) = 1. По теореме Лагранжа (о порядках групп) группа Э может иметь собственные подгруппы, 2-го и 4-го порядков. Элементы группы 8-го порядка (11,19 и 29) имеют 2-й порядок; (7,13, 17, 23) 4-й порядок и единица. Подгрупп 4-го порядка имеется три: одна (1,11,19,29) – включает только инволюции, и две подгруппы циклические:
7 × 7 ≡ 49 (mod30) = 19; 19 × 7 ≡ 133(mod30) = 13; 13 × 7 ≡ 91 (mod30) = 1;
11× 19 ≡ 209 (mod30) = 29; 11 ×29 ≡ 319(mod30) = 19; 19 ×29 ≡ 551 (mod30) = 1;
17× 17 ≡ 289 (mod30) = 19; 19 ×17 ≡ 323(mod30) = 23; 23 × 17≡ 391 (mod30) =1;
Как ни удивительно, но все числа 24 классов |Т(S, Ф) | = 3×8 преобразуются в семейство классов, состоящее всего из 8 классов, порождаемых каждым представителем множества р(i). В новых классах числа — элементы следуют с периодом уже не 90, а в три раза меньшим, всего лишь 30.
Таблица 2 — Мультипликативные подгруппы группы вычетов (pk)по mod30
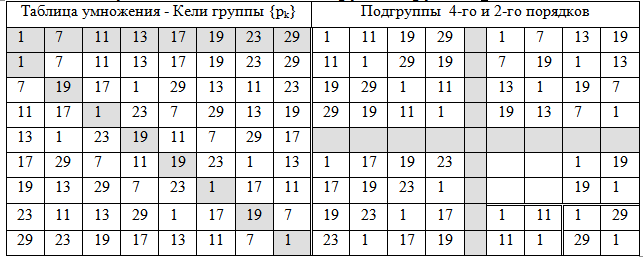
Классы формируются с учетом флексии и свертки чисел по три пары (2,1),(5,1),(8,1); (4,1),(7,1),(1,1); (2,3),(5,3),(8,3); (4,3),(7,3),(1,3); (7,7),(1,7),(4,7); (8,7),(2,7),(5,7); (7,9),(1,9),(4,9);(8,9),(2,9),(5,9);
Ниже в таблице 3 приведем начальные фрагменты этих 8 классов. Любое нечетное число N >31 не кратное 3 или 5 имеет вид N = p(i)+ 30t и попадает в один из 8 классов, представленных в таблице 3. Назовем множество чисел из такой таблицы множеством Т — 8.
Таблица 3 — Классы чисел с периодом 30. Простые числа {pk} выделены заливкой
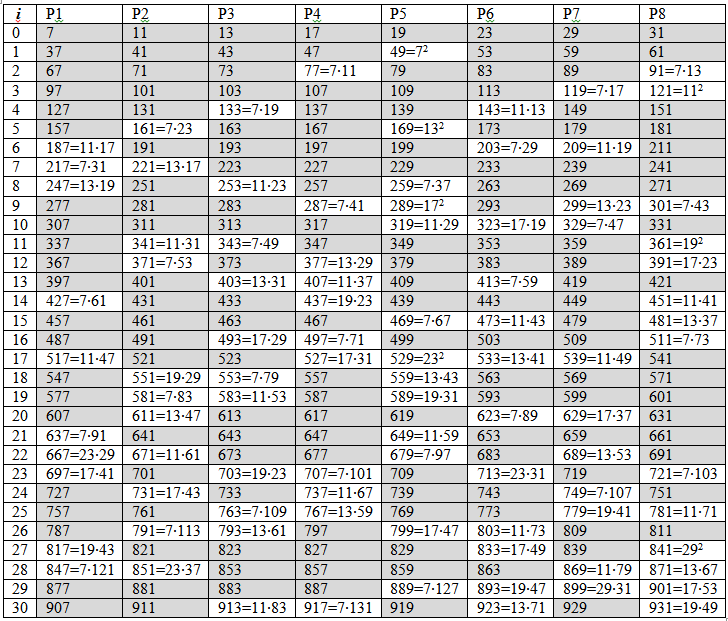
Даже поверхностный анализ таблицы позволяет сделать некоторые выводы в отношении простоты-сложности и возможности факторизации чисел:
– все степени всех генераторов классов, т.е. простых чисел – составные;
– строки с номером кратным генератору в клетке столбца этого генератора содержат составные числа, делитель которых генератор;
– числа, принадлежащие области запрета простых чисел в спирали Улама, – составные, примеры таких чисел в первой тысяче:143,161,203,217,323,451, 517,539,473, 611,637 и др.
– числа, допускающие разложение в сумму- разность и вынесение за скобку общего множителя, например, 217 =210+7 =7(30 +1) =7×31; 1397 = 1270 +127 = 127(10 +1) = 127×11.
Таким образом, элементарными средствами и операциями удается селектировать множество Т-8 нечетных чисел НРЧ, которые должны и могут служить объектом последующего исследования в интересах решения как теоретических, так и прикладных практических задач. К числу таких задач в области криптологии и информационной безопасности следует отнести следующие: ЗФБЧ, задачу установления простоты числа, задачу дискретного логарифма в конечных полях и группах точек эллиптических кривых.
Множество чисел Т-8 организовано специальным образом (состоит из 8 классов), наименьшие представители классов образуют группу вычетов по модулю 30 (φ(30) = 8 ). Это свойство обеспечивает определение номера столбца результата произведения пары чисел, номера столбцов которых известны. Таблица Кели группы обеспечивает решение этой задачи.
Назначение примеров показать, какая информация о связях значений чисел, номеров строк и номеров столбцов содержится в множестве Т- 8.
Один из возможных методов факторизации чисел множества Т-8 с использованием таблицы 3.
Пример 2. Пусть задано составное нечетное натуральное число (сннч)
N = 1727. Требуется факторизовать его. Найдем положение этого числа в множестве Т-8: номер строки N/ 30 = 57 (берется целая часть дроби), номер (имя) столбца N – 30∙57 = 17. В этом же столбце задаем произведение 7∙11=77, номер строки которого равен 2.
Пробуем сохранить каждый из делителей. Сохраняем d1 = 7, другой делитель N приобретает вид
d2 = 11 + 30∙t, где t определяется через разность номеров строк и сохраняемый делитель
t = (57 – 2)/7 = 7,85. Получили дробное значение, из чего следует, что 7 не является делителем заданного числа 1727. На самом деле можно сразу пробным делением выяснить является ли di делителем заданного числа.
Сохраняем d2 = 11, другой делитель приобретает вид d1 = 7 + 30∙t, где t определяется через разность номеров строк и сохраняемый делитель t = (57 – 2)/11 = 5. Тогда d1 = 7 + 30∙t = 157.
Действительно, 1727/157 = 11.
Пример 3.Пусть задано составное нечетное натуральное число (сннч)
N = 4294967297, вне пределов таблицы. Требуется факторизовать его. Найдем как и ранее положение этого числа в множестве Т-8:
номер строки N/ 30 = 143165576,
номер столбца N – 30∙143165576 = 17.
В этом же столбце задаем произведение 7∙641 = 4487, номер строки которого равен 149.
Пробуем сохранить каждый из делителей. Сохраняем d1 = 641, другой делитель приобретает вид
7 + 30∙t, где t определяется через разность строк и сохраняемый делитель
t = (143165576 – 149)/641 = 143165427/641 = 223347.
Значение t = 223347 – целое число, следовательно, 641 – делитель исходного числа N.
Действительно, N/d1 = 4294967297:641 = 6700417 — простое число (другой делитель).
Автор: VAE





