Моя трёхлетняя дочка София в последнее время частенько упоминает «ноль», например, в таком контексте:
— Соня, вот ты вроде сначала не послушалась, а затем послушалась, что же получается?..
— Ну… ноль!
Т.е. ощущение отрицательных чисел и нейтральности нуля уже имеет, о как. Скоро поинтересуется: почему же это на ноль делить нельзя?
И вот решил я простыми словами записать всё, что я ещё помню про деление на ноль и всё такое.
Деление вообще лучше один раз увидеть, чем сто раз услышать.
Ну, или один разделить на икс раз увидеть…
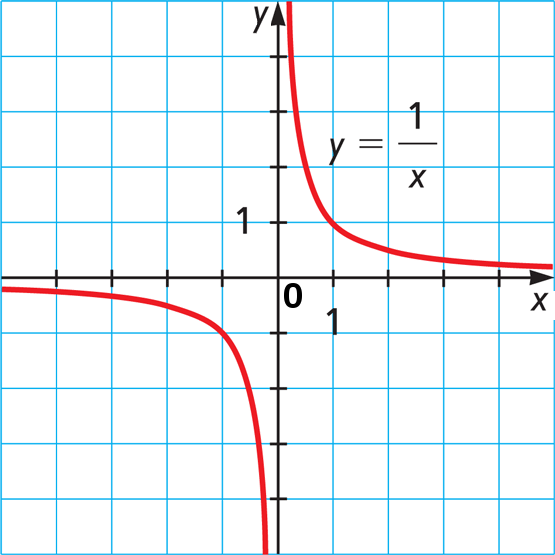
Тут сразу видно, что ноль — это центр жизни, вселенной и всего такого. Ответом на главный вопрос про всё это пусть себе будет 42, а вот центр — по-любому 0. У него даже знака нет, ни плюс (послушалась), ни минус (не послушалась), он таки реально ноль. И в поросятах знает толк.
Потому что если любого поросёнка умножить на ноль, то поросёнка засасывает в эту круглую чёрную дыру, и получается опять ноль. Не такой уж этот ноль и нейтральный, когда дело от сложения-вычитания доходит до умножения, не говоря уже про деление… Там если ноль сверху «0/x» — то опять чёрная дыра. Всё поедает в ноль. А вот если при делении, да ещё и снизу — «x/0», то начинается… следуй за белым кроликом, Соня!
В школе тебе скажут «на ноль делить нельзя» и не покраснеют. В доказательство тыкнут на калькуляторе «1/0=» и обычный калькулятор, тоже не покраснев, напишет «E», «Error», мол, «нельзя — значит нельзя». Хотя что там у тебя будет считаться обычным калькулятором — ещё вопрос. Мне вот сейчас, в 2014-ом, стандартный калькулятор на телефоне-андроиде пишет совсем другое:

Ничего себе бесконечность. Скользи себе взглядом, круги нарезай. Вот тебе и нельзя. Оказывается можно. Если осторожно. Потому что не осторожно мой Android пока тоже не согласен: «0/0=Error», опять нельзя. Попробуем ещё разок: «-1/0 = -∞», о как. Интересное мнение, но я с ним не согласен. Как не согласен и с «0/0=Error».
Кстати, JavaScript, который питает нынешние сайты, тоже не согласен с калькулятором андроида: зайди в консоль браузера (ещё F12?) и напиши там: «0/0» (ввод). JS тебе ответит: «NaN». Это не ошибка. Это «Not a Number» — т.е. какая-то штука такая, но не число. При том что «1/0» JS тоже понимает как «Infinity». Это уже ближе. Но пока только тепло…
В университете — высшая математика. Там пределы, полюса, и прочее шаманство. И всё усложняется, усложняется, ходят вокруг да около, но только бы не нарушать хрустальные законы математики. А вот если не пытаться вписать деление на ноль в эти существующие законы, то можно прочувствовать эту фантастику — на пальцах.
Для этого посмотрим-ка ещё раз на деление:
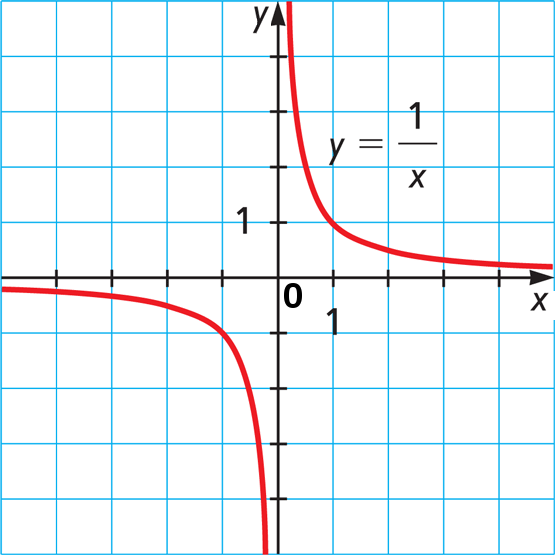
Следи за правой линией, справа налево. Чем ближе икс к нулю, тем сильнее взлетает вверх разделённое на икс. И где-то там в облаках «плюс бесконечность». Она всегда дальше, как горизонт, её не догонишь.
А теперь следи за левой линией, слева направо. Та же история, только теперь разделённое улетает вниз, бесконечно вниз, в «минус бесконечность». Отсюда и мнение, что «1/0= +∞», а «-1/0 = 1/-0 = -∞».
Но фокус в том, что «0 = -0», нету у нуля знака, если не усложнять с пределами. И вот если поделить единицу на такой «простой» ноль без знака, то не логично ли предположить, что получится и бесконечность — «просто» бесконечность, без знака, как ноль. Где она — сверху или снизу? Она везде — бесконечно далеко от нуля во всех направлениях. Это и есть ноль, вывернутый наизнанку. Ноль — нет ничего. Бесконечность — есть всё. И положительное, и отрицательное. Вообще всё. И сразу. Абсолют.
Но там что-то было про «0/0», что-то другое, не бесконечность… Сделаем такой трюк: «2*0=0», ага, скажет учительница в школе. Ещё: «3*0=0» — опять ага. И немного наплевав на «на ноль делить нельзя», мол, весь мир и так потихоньку делит, получим: «2=0/0» и «3=0/0». В каком там классе это проходят, только без нуля, конечно.
Минуточку, получается «2 = 0/0 = 3», «2=3»?! Вот поэтому и боятся, вот поэтому и «нельзя». Страшнее «1/0» только «0/0», его даже калькулятор андроида боится.
А мы не боимся! Потому что у нас есть сила математики воображения. Мы можем представить себя бесконечным Абсолютом где-то там в звёздах, посмотреть оттуда на грешный мир конечных чисел и людей и понять, что с этой точки зрения они все одинаковые. И «2» c «3», и даже «-1», и училка в школе, возможно, тоже.
Так вот, я скромно предполагаю, что 0/0 — это весь конечный мир, точнее всё, что и не бесконечно и не пустота.
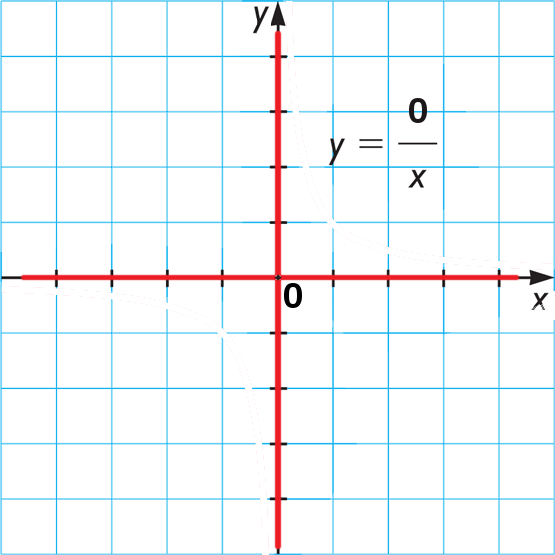
Вот как выглядит ноль, делённый на икс, в моих фантазиях, далёких от официальной математики. На самом деле похоже на 1/х, только перегиб не в единице, а в нуле. Кстати, у 2/x перегиб в двойке, а у 0.5/x — в 0.5.
Получается, 0/x при x=0 принимает все конечные значения — не бесконечности, не пустоту. Там в графике дырочка в нуле, оси проглядывают.
Можно конечно возразить, что «0*0 = 0», а значит ноль (пустота) тоже попадает в категорию 0/0. Чуть забегу вперёд — там будут степени нуля и это возражение разлетится в осколки.
В таких божественных категориях есть лишь пустота (0), конечный мир (0/0), и бесконечность (1/0).
Упс, единичка-то в бесконечности тоже может быть тоже записана как 0/0, получится (0/0)/0 — бесконечность. Вот теперь порядок, всё можно выразить соотношением нулей.
И эти категории подчиняются многим законам обычных чисел, показывая весьма интересные отношения.
Например, если к бесконечности прибавить конечное, то бесконечность поглотит конечное, останется бесконечностью:
1/0 + 0/0 = (1+0)/0 = 1/0.
А если бесконечность умножить на пустоту, то они поглощают друг друга, и получается конечный мир:
1/0 * 0 = (1*0)/0 = 0/0.
Но это только первый уровень сновидений. Можно копать глубже.
Если ты уже знаешь понятие «степень числа», и что «1/x = x^-1», то, подумав, сможешь перейти от всех этих делений и скобок (вроде (0/0)/0) просто к степеням:
1/0 = 0^-1
0/0 = 0^0
0 = 0^1
Подсказка.
Тут с бесконечностью и пустотой всё просто, как в школе. А конечный мир переходит к степеням вот так:
0/0
= (0*1)/0
= 0*(1/0)
= 0 * 1/0
= 0^1 * 0^-1
= 0^(1 + -1)
= 0^(1-1)
= 0^0.
Уфф!
Получается, что положительные степени нуля — это нули, отрицательные степени нуля — это бесконечности, а нулевая степень нуля — это конечный мир.
Такой вот получается универсальный объект «0^x». Такие объекты прекрасно между собой взаимодействуют, опять-таки многим законам подчиняются, красота, в общем.
Моих скромных познаний математики хватило, чтобы нарисовать из них абелеву группу, которая, будучи изолированной в вакууме («просто абстрактные объекты, такая форма записи, вроде экспоненты»), даже выдержала проверку крутейшим преподом по матану с вердиктом «интересно, но ничего не получится». Ещё бы тут что-нить получилось, это ж табуированная тема — деление на ноль. В общем, не грузись.
Попробуем лучше просто умножить бесконечность на конечное число:
0^-1 * 0^0 = 0^(-1 + 0) = 0^-1.
Опять же, бесконечность поглотила конечное число так же, как и её антипод ноль поглощает конечные числа, та же чёрная дыра:
0^1 * 0^0 = 0^(1 + 0) = 0^1.
А ещё оказывается что степени — это как сила. Т.е. ноль второй степени сильнее нуля обычного (первой степени, 0^1). И бесконечность минус второй степени сильнее бесконечности обычной (0^-1).
А когда пустота сталкивается с абсолютом, они меряются силой — у кого больше, тот и победит:
0^1 * 0^-2 = 0^(1 + -2) = 0^-1 = ∞.
0^2 * 0^-1 = 0^(2 + -1) = 0^1 = 0.
Если же они равны силами, то аннигилируются и остаётся конечный мир:
0^1 * 0^-1 = 0^(1 + -1) = 0^0.
Кстати, официальная математика уже рядом. Её представители знают про «полюса» и что у полюсов разная сила (порядок), а так же про «нуль порядка k». Но они всё топчутся на прочной поверхности «рядом с» и боятся прыгнуть в чёрную нору дыру.
И последний для меня — третий уровень сновидений. Вот, например, эти все 0^-1 и 0^-2 — бесконечности разной силы. Или 0^1, 0^2 — нули разной силы. Но ведь и «-1» и «-2» и «+1» и «+2» — это всё — 0/0, равное 0^0, уже проходили. Получается, что с этого уровня сновидений, уже всё равно вообще что это — нули, бесконечности, и даже конечный мир туда при некотором просветлении попадает. В одну точку. В одну категорию. Называется это счастье — Сингулярность.
Надо признать, что вне состояния просветления одной точки я не наблюдаю, но одну категорию — объединение «0^0 U 0^(0^0)» — вполне.
Какую из всего этого можно вынести пользу? Ведь даже чуть менее безумные «мнимые числа», что тоже рвут калькуляторы в Error = √-1, и те смогли стать официальной математикой и теперь упрощают расчёты сталеварения.
С делением на ноль и категориями 0^x польза, скорее, философская. Увидеть, как бесконечности и пустоты поглощают конечное, как пустота может победить бесконечность, а может случиться и наоборот.
Как листья на дереве издалека кажутся одинаковыми, но если рассмотреть их внимательнее — они все разные. А если задуматься, то опять одинаковые. И мало чем отличаются от тебя или меня. Вернее, вообще ничем не отличаются, если крепко задуматься.
Польза тут в умении и фокусироваться на отличиях и абстрагироваться. Это очень полезно и в работе, и в жизни, и даже в отношении к смерти.
Вот такие путешествия в кроличью нору, Соня!
Автор: denis-ryzhkov






