Плотностный алгоритм кластеризации пространственных данных с присутствием шума — DBSCAN

Доброго времени суток!
Хотел бы с вами поделиться реализацией в MATLAB плотностного алгоритма для кластеризации пространственных данных с присутствием шума — DBSCAN (Density Based Spatial Clustering of Applications with Noise).

Особенности

Алгоритм DBSCAN был предложен Мартином Эстер, Гансом-Питером Кригель и коллегами в 1996 году как решение проблемы разбиения (изначально пространственных) данных на кластеры произвольной формы. Большинство алгоритмов, производящих плоское разбиение, создают кластеры по форме близкие к сферическим, так как минимизируют расстояние документов до центра кластера. Авторы DBSCAN экспериментально показали, что их алгоритм способен распознать кластеры различной формы.

Основная идея

Идея, положенная в основу алгоритма, заключается в том, что внутри каждого кластера наблюдается типичная плотность точек (объектов), которая заметно выше, чем плотность снаружи кластера, а также плотность в областях с шумом ниже плотности любого из кластеров. Ещё точнее, что для каждой точки кластера её соседство заданного радиуса должно содержать не менее некоторого числа точек, это число точек задаётся пороговым значением. Для детального изложения принципиальных особенностей алгоритма необходимо ввести ряд определений — ознакомиться с которыми более подробно можно в прекрасном учебном пособии [1] на стр. 197-200, где также приведен данный алгоритм в общем виде. Я же предлагаю вам обратить свое внимание непосредственно на реализацию идей предложенных авторами.

Входная /выходная информация

Входной информацией является матрица cont размерностью n x 4. В первых двух столбцах располагаются координаты рассматриваемых точек, два других столбца заполняются 0.
В результате работы алгоритма заполняются столбцы 3 и 4 матрицы cont: 3-ий столбец отражает информацию о том была ли обработана точка; 4-ый столбец отвечает за принадлежность к тому или иному классу от 1 до с-1. Если в 4ом столбце записано -1 значит эта точка была отнесена к шуму.

Реализация в пакете MATLAB

n = length(cont(:,1)); %% определяем количество точек
L_min = 30; %% максимальный размер области
L = zeros(n,n); %% создаем пустую матрицу
Rez = zeros(n,1);  %% создаем пустую матрицу
for i=1:1:n
    %% рассчитываем какие точки находятся на расстоянии < L_min от текущей %
    L(:,i)=sqrt((cont(:,1)-cont(i,1)).^2 + (cont(:,2)-cont(i,2)).^2)<=L_min; 
    %% определяем количество точек находящихся на расстоянии < L_min от текущей точки %
    Rez(i) = sum(L(:,i))-1; 
    L(:,i)=L(:,i).*(1:1:n)'; %% отмечаем номера этих пикселей находящихся на расстоянии < L_min от текущей точки
end
kol=5; %% задаем требуемое количество точек находящихся на расстоянии < L_min от текущей точки
c=1; %% инициируем счетчик групп
for i=1:1:n
    if cont(i,3) == 0 %% если точка не отмечена как "отмечено" 
        if Rez(i)<kol %% если количество точек на расстоянии < L_min, меньше то помечаем точку как шум
            cont(i,3)=1; %% отмечаем что "отмечено"
            cont(i,4)=-1; %% помечаем как шум
        else %% если количество точек на расстоянии < L_min, больше то исследуем дальше
            uvec = cont(:,4); %% запоминаем текущее состояние вектора разделеия по группам
            cont(i,4)=c; %% помечаем текущую точку как принадлежащую текущей группе с
            while sum(uvec-cont(:,4))~=0 %% пока вектор разделения по группа не прекратит изменяться
                uvec = cont(:,4); %% запоминаем текущее значение вектора разделеия по группам
                for j=1:1:n %% пробегаем по всему вектору
                    if cont(j,4)==c && cont(j,3)==0 %% если точка отнесена к какому либо классу но не "помечена"
                        if Rez(j)<kol %% и вокруг нее на расстоянии менее L_min количество точек меньше чем kol
                            cont(j,3)=1; %% отмечаем что отмечено
                            cont(j,4)=-1; %% помечаем как шум
                        else %% иначе
                            cont(j,3)=1; %% отмечаем что "отмечено"
                            cont(find(L(j,:)>0),4)=c; %% и все точки находящиеся на расстоянии менее L_min помечаем как относящиеся к этой группе
                        end
                    end;
                end;
            end;
            c=c+1; %% увеличиваем счетчик групп
        end;
    else
        continue
    end;
end;

Извиняюсь за некорректную подсветку кода MATLAB, так и не смог разобраться с ней на HABRAHABR.

Результаты работы

Пусть исходной информацией для алгоритма является набор точек (см. рисунок ниже), содержащий помимо 3-ех явно выделяющихся групп, точки которые необходимо отнести к шуму.

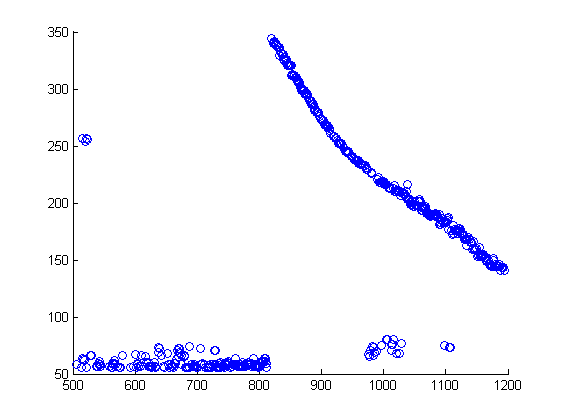
После работы алгоритма получаем следующую картину кластеризации:

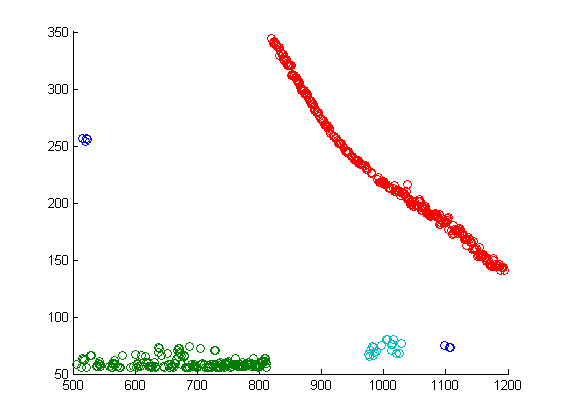
Как видно, алгоритм выделил 3 группы и шум (синие scatter на изображении) чего и следовало ожидать! Внимание читателя также хочется обратить на то, что алгоритм прекрасно справился с задачей выделения точек расположенных по некоторой кривой, что позволяет, при должном применении, использовать данный алгоритм для задачи выделения контуров объектов на изображении… но эта уже совсем другая история!

Литература

Автоматическая обработка текстов на естественном языке и компьютерная лингвистика: учеб. пособие / Большакова Е.И., Клышинский Э.С., Ландэ Д.В., Носков А.А., Пескова О.В., Ягунова Е.В. — М.: МИЭМ, 2011. — 272 с.

Автор: Perfer, источник