Примечание: Данный текст публикуется в рамках эксперимента — в нашем блоге мы осветили уже довольно большое количество вводных теоретических аспектов фондового рынка. Сегодня мы попытаемся «перейти на следующий уровень» и поговорить о более глубокой и сложной теме — индексах волатильности, в частности, подобного индекса для российского рынка.
16 апреля 2014 года Московская Биржа запустила расчет и публикацию нового индекса волатильности российского рынка — индекса RVI.
В пресс-релизе биржи по случаю запуска индекса RVI указано, что:
Новый индекс позволяет оценить уровень волатильности российского рынка, а также расширяет финансовые возможности опционных трейдеров, хеджеров и институциональных инвесторов.
Индекс RVI рассчитывается согласно пяти основным принципам:
- Индекс рассчитывается для получения значений тридцатидневной волатильности;
- Расчет осуществляется на основе двух серий опционов на фьючерс на Индекс РТС, а именно: опционы ближайшей и следующей серий, входящие в квартальную или месячную серии, но не входящие в недельную серию, срок до даты экспирации которых включительно составляет более 7 дней;
- В расчет индекса также входят котировки фьючерсов, являющихся базовым активом опциона ближайшей серии и опциона следующей серии.
- В случае отсутствия котировок и сделок предусмотрена возможность расчета Индекса RVI по теоретической цене опциона, определяемой на основании котировки фьючерса, являющегося базовым активом такого опциона, и кривой волатильности на момент расчета;
- Индекс рассчитывается каждые 15 секунд в течение основной и вечерней торговых сессий на Срочном рынке (с 10:00 до 18:45 и с 19:00 до 23:50 мск).
Согласно «Методике расчета Индекса волатильности российского рынка», утвержденной решением Правления ОАО Московская Биржа (Протокол №24 от 11 апреля 2014 г.), индекс RVI рассчитывается по формуле:
$latex RVI=100times sqrt {frac{T_{365}}{T_{30}}left| T_{1}sigma_{1}^{2}left( frac{T_{2}-T_{30}}{T_{2}-T_{1}} right)+T_{2}sigma_{2}^{2}left( frac{T_{30}-T_{1}}{T_{2}-T_{1}} right) right|}$
(Формула 1),
где
$latex T_{365}$ – 365 дней в долях от календарного года (год = 365 дней);
$latex T_{30}$ – 30 дней в долях от календарного года (год = 365 дней);
$latex T_{1}$ – время до даты экспирации ближайшей серии опционов включительно в долях от календарного года (год = 365 дней);
$latex T_{2}$ – время до даты экспирации следующей серии опционов включительно в долях от календарного года (год = 365 дней);
$latex sigma_{1}$ – подразумеваемая волатильность ближайшей серии опционов;
$latex sigma_{2}$ – подразумеваемая волатильность следующей серии опционов.
Волатильности ближайшей и следующей серий опционов определяются уравнениями:
$latex sigma^2_1=frac{2}{T_1}sum_{i=-7}^{7}{frac{triangle K_i}{K^2_i}Prleft(K_iright)}-frac{1}{T_1}{left(frac{F_1}{K_0}-1right)}^2$
(2)
$latex sigma^2_2=frac{2}{T_2}sum_{i=-7}^{7}{frac{triangle K_i}{K^2_i}Prleft(K_iright)}-frac{1}{T_2}{left(frac{F_2}{K_0}-1right)}^2$
(3)
где
$latex triangle K_i$ — шаг страйка (в целях расчета Индекса используются основные страйки, промежуточные страйки не используются);
$latex T_1$ — время до даты экспирации опциона ближней серии включительно в долях от календарного года (год = 365 дней). Изменяется каждые 15 секунд;
$latex T_2$ — время до даты экспирации опциона дальней серии включительно в долях от календарного года (год = 365 дней). Изменяется каждые 15 секунд;
$latex K_i$ — i-й страйк. При этом (в целях расчета Индекса используются основные страйки, промежуточные страйки не используются);
$latex F_1, F_2$ — котировки фьючерсных контрактов, являющихся базовым активом опциона ближайшей серии и опциона следующей серии соответственно.
Котировка фьючерсного контракта равна либо цене последней сделки, либо цене лучшей активной заявки на продажу, которая меньше цены последней сделки, либо цене лучшей активной заявки на покупку, которая больше цены последней сделки в текущий момент. В случае если сделок в текущей сессии до момента расчета котировки фьючерсного контракта не было, используется среднеарифметическое значение между ценами лучшей активной заявки на покупку и лучшей активной заявки на продажу. Если на момент расчета активные заявки на покупку и активные заявки на продажу отсутствуют, используется расчетная цена, определенная по итогам ближайшего предыдущего расчетного периода.
$latex Prleft(K_iright)$ — стоимость опциона для i-го страйка, определяемая по определенному алгоритму [1].
Подробно с методикой расчета индекса RVI можно ознакомиться на сайте Московской Биржи в разделе «Индексы/Индекс волатильности». К сожалению там вы не найдете ссылок на ресурсы, объясняющие каким образом получены указанные выше формулы, и какой они несут экономический смысл. Для поиска первоисточников обратимся к методике расчета индекса волатильности Чикагской Биржи CBOE — VIX.
The CBOE Volatility Index — VIX
В 1993 году Chicago Board Options Exchange (CBOE) начала рассчитывать и публиковать значения CBOE Volatility Index (VIX). Данный индекс волатильности был создан для оценки рыночных ожиданий относительно 30-дневной волатильности и рассчитывался с использованием рыночных цен at-the-money опционов на S&P 100 Index (OEX). Спустя 10 лет в 2003 году CBOE совместно с Goldman Sachs обновила методику расчета VIX. Новый VIX основан на S&P 500 Index (SPX) и оценивает ожидаемую волатильность с помощью усреднения цен опционов на SPX, выбранных по широкому списку страйков с определенными весами. Позволяя выражать показатель волатильности через портфель SPX опционов, новая методология трансформировала VIX из абстрактной концепции в практический стандарт торговли и хеджирования волатильности.
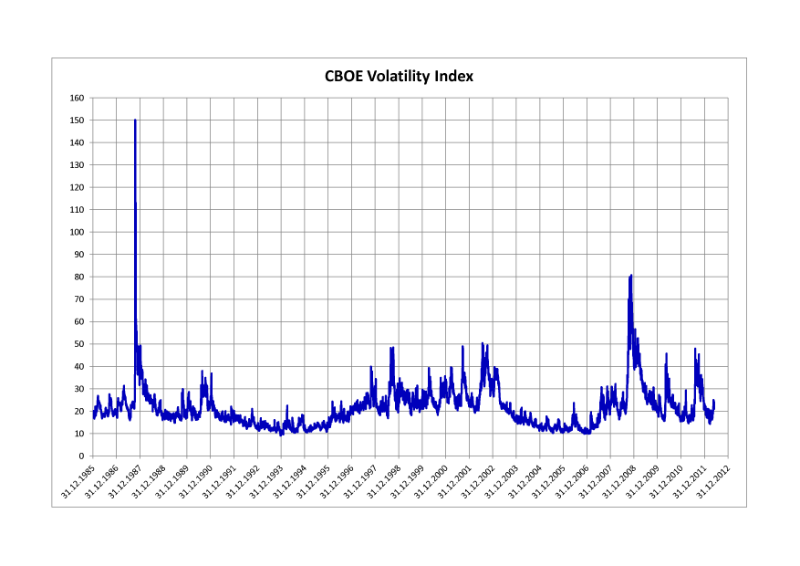
В марте 2004 года CBOE выводит на биржу первый фьючерсный контракт на VIX. Двумя годами позже в феврале 2006 CBOE запускает VIX опционы, самый успешный продукт в истории биржи [2].
Напомню, что Московская Биржа в лице Романа Сульжика в апреле текущего года сообщила, что планирует этим летом запустить фьючерсный контракт на индекс волатильности RVI. Будем надеяться, что это произойдет в заявленные сроки, и что новый продукт будет востребован рынком.
Обобщенная формула для расчета VIX имеет вид:
$latex sigma^2=frac{2}{T}sum_i{frac{triangle K_i}{K^2_i}e^{RT}Qleft(K_iright)}-frac{1}{T}{left(frac{F}{K_0}-1right)}^2$
(4)
где
$latex sigma$ — VIX/100;
$latex T$ — время до экспирации (в годах);
$latex F$ — цена форварда на индекс S&P 500, получаемая из цен опционов SPX;
$latex K_0$ — страйк ближайший снизу к цене форварда на индекс;
$latex K_i$ — страйк i-го out-of-the-money опциона call, если $latex K_i>K_0$, или put, если $latex K_i<K_0$, и обоих put и call, если $latex K_i=K_0$;
$latex triangle K_i$ — интервал между страйками, половина разницы между страйками с каждой стороны от $latex K_i$:
$latex triangle K_i=frac{K_{i+1}-K_{i-1}}{2}$
Замечание: $latex triangle K$ для самого нижнего страйка равен разнице между самым нижним страйком и следующим страйком. Для самого верхнего страйка — разница между самым верхним и предыдущим.
$latex R$ — безрисковая ставка к экспирации;
$latex Qleft(K_iright)$ — среднее значением между ценами bid и ask для опциона со страйком $latex K_i$, для $latex K_0$ — это среднее цен bid и ask двух опционов put и call.
VIX измеряет 30-дневную ожидаемую волатильность индекса S&P 500. Компонентами VIX являются опционы call и put ближней и следующей серий, обычно это первый и второй месячные контракты SPX. Ближняя серия должна иметь срок как минимум одну неделю до экспирации. Для каждой выбранной опционной серии вычисляется квадрат волатильности — $latex sigma^2_1$ и $latex sigma^2_2$ по формуле (4). Далее находится их 30-дневное взвешенное среднее по формуле:
$latex VIX=100times sqrt{left{T_1sigma^2_1left[frac{N_{T_2}-N_{30}}{N_{T_2}-N_{T_1}}right]+T_2sigma^2_2left[frac{N_{30}-N_{T_1}}{N_{T_2}-N_{T_1}}right]right}times frac{N_{365}}{N_{30}}}$
(5)
Сопоставив формулы (1 — 3) и (4 — 5) между собой, приходим к выводу, что индекс волатильности Московской Биржи RVI является точной копией индекса Чикагской опционной биржи VIX. Отличие RVI от VIX лишь в отсутствии фактора роста $latex e^{RT}$, а также в способе определения опционов, участвующих в расчетах, и их цен. Первое следует из того, что в расчетах индекса RVI участвуют опционы на фьючерсный контракт, а не equity актив как у VIX. Последнее, вероятно, продиктовано низкой ликвидностью российского опционного рынка.
Документ CBOE [2], раскрывающий методику расчета VIX, содержит ссылку на материалы компании Goldman Sachs [3], в которых приводится описание способов оценки Volatility Swap и Variance Swap. Математика VIX тесно переплетена с математикой прайсинга свопов волатильности. И это не случайно, т.к. новый VIX (запущенный в 2003 г.) разрабатывался CBOE совместно с инвестиционным банком Goldman Sachs. Последний в свою очередь активно продвигал торговлю свопами на волатильность — в 1999 году была опубликована знаменитая статья «More than you ever wanted to know about volatility swaps», в которой авторы — количественные аналитики из Goldman Sachs дали описание методики оценки стоимости этих свопов. Идея создать индекс волатильности, привязанный к реальному инструменту, денежный поток которого напрямую зависит от этой волатильности, оказалась весьма успешной — фьючерсы и опционы на VIX приобрели большую популярность среди инвесторов.
Variance Swap
Как отмечено выше, методика расчета индекса VIX тесно связана с теорией свопов волатильности. Основой данного класса финансовых инструментов является понятие Variance Swap. Variance Swap (VS) — это форвардный контракт на годовую дисперсию (variance), квадрат реализованной волатильности (realized volatility). Формула выплаты на экспирацию по данному свопу описывается формулой:
$latex left(sigma^2_R-K_{var}right)times N$
(6)
где
$latex sigma^2_R$ — реализованная дисперсия акции, фьючерса, индекса и т.п., указанная в годовом выражении, за период обращения контракта;
$latex K_{var}$ — цена поставки контракта;
$latex N$ — номинал свопа на единицу годовой дисперсии.
Владелец VS при экспирации контракта получит N долларов за каждый пункт, на который реализованная дисперсия $latex sigma^2_R$ превысит цену поставки $latex K_{var}$. Поэтому справедливое значение дисперсии (по мнению рынка) равно цене поставки VS, при которой стоимость свопа будет нулевой. Справедливое значение дисперсии в данном контексте служит хорошим ориентиром для значения индекса волатильности VIX. Таким образом, методику оценки стоимости VS можно применять и в расчетах VIX.
Оценка стоимости VS производится с помощью стратегии репликации свопа через портфель опционов. В основе данной стратегии лежит понятие log-контракта — экзотического опциона на акцию (индекс, фьючерс и т.п.), хеджирование которого обеспечивает выплату эквивалентную дисперсии доходностей цен этой акции. Log-контракт в свою очередь может быть реплицирован через портфель ванильных опционов на тот же базовый актив. Это дает возможность выразить стоимость VS через цены опционов.
Обозначим $latex V$ показатель чувствительности цены опциона $latex C_{BS}$ к дисперсии базового актива $latex sigma^2$ (назовем его Variance Vega), определяющий на сколько изменится цена опциона в случае изменения дисперсии его базового актива:
$latex V=frac{partial C_{BS}}{partial sigma^2}$
(7)
На Рисунке 1 представлены графики изменения показателя Variance Vega для опционов с различными страйками в зависимости от цены базового актива (левая часть), а также графики Variance Vega портфелей, состоящих из этих опционов (правая часть).
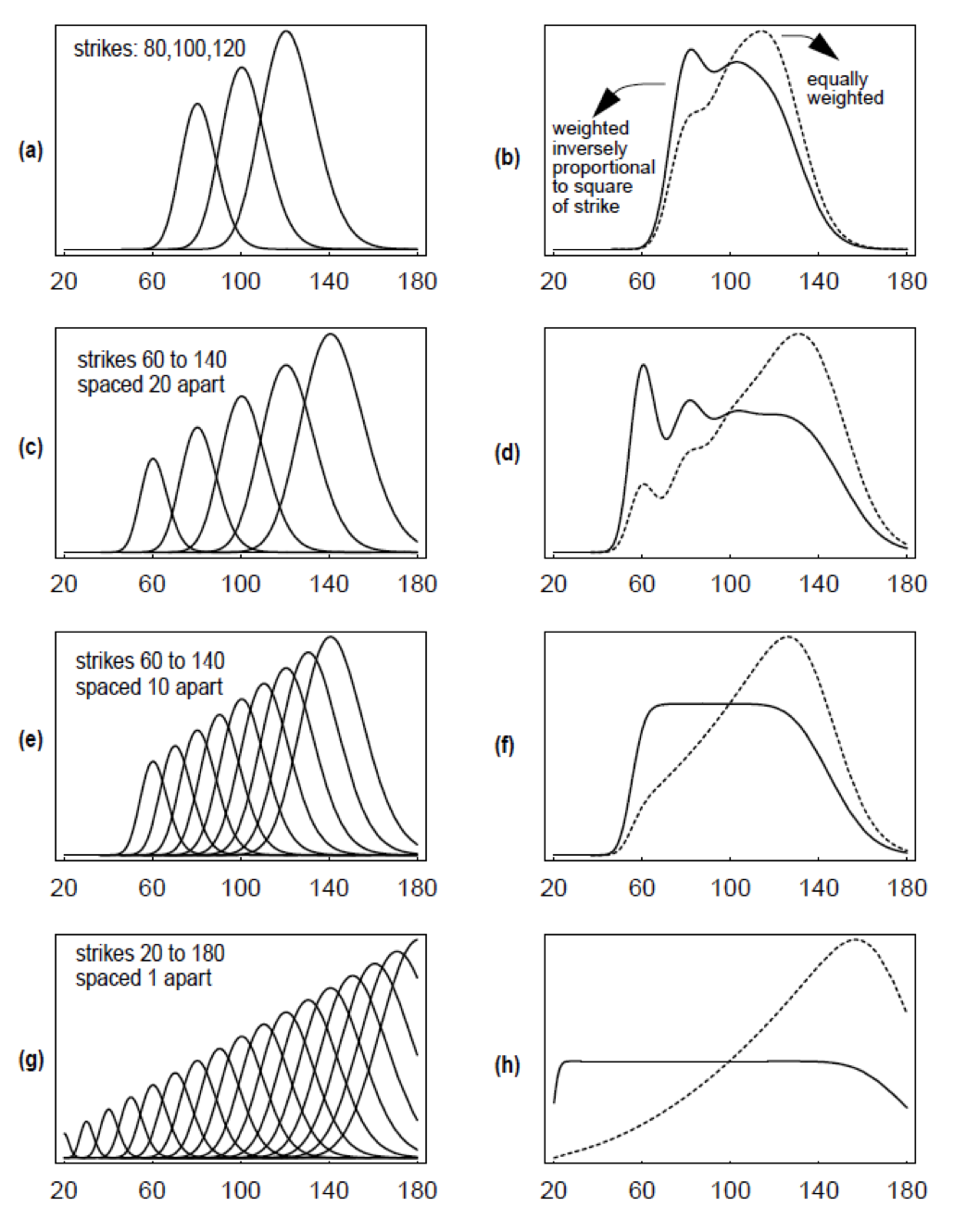
Рис. 1: Variance Vega портфелей call опционов с различными страйками как функция цены базового актива. Каждый график слева показывает вклад отдельного опциона в V портфеля. Соответствующий ему график справа показывает сумму этих вкладов, взвешенных двумя способами: штриховая линия — с равными весами, сплошная линия — с весами обратно пропорциональными квадрату страйка. Число опционов увеличивается, а расстояние между страйками уменьшается от верхнего графика к нижнему
Таким образом, Variance Vega портфеля, состоящего из опционов всех страйков, взвешенных обратно пропорционально квадрату страйка, не зависит от цены базового актива. Это как раз то, что нужно для торговли дисперсией. Как выглядит подобный портфель опционов, и каким образом торговля этим портфелем зависит от дисперсии базового актива?
Рассмотрим портфель $latex Pi left(S, sigma, tauright)$, состоящий из опционов со всеми страйками K с одинаковым сроком до экспирации $latex tau$, взвешенными обратно пропорционально квадрату K. В виду того, что out-of-the-money опционы, как правило, более ликвидны, будем использовать put опционы $latex Pleft(S, K, sigma, tauright)$ для страйков K, принимающих значения от 0 до некоторой ориентировочной цены $latex S_*$, и call опционы $latex Cleft(S, K, sigma, tauright)$ для страйков от $latex S_*$ до бесконечности. Цену $latex S_*$ можно рассматривать как at-the-money уровень форварда на базовый актив (или цену фьючерса) со сроком $latex tau$, обозначающий границу между ликвидными put и call опционами.
В момент экспирации, когда t=T, можно показать, что суммарная выплата всех опционов указанного выше портфеля равна:
$latex Pi left(S_T,0right)=frac{S_T-S_*}{S_*}-log frac{S_T}{S_*}$
(8)
Аналогично, в момент времени t, просуммировав все цены опционов, стоимость портфеля составит:
$latex Pi left(S_t, sigma, tauright)=frac{S_t-S_*}{S_*} - log frac{S_t}{S_*} + frac{sigma^2 tau}{2}$
(9)
Variance Vega данного портфеля:
$latex V=frac{tau}{2}$
(10)
Чтобы получить начальную Variance Vega в размере $1 на единицу квадрата волатильности необходимо открыть (2/T) единиц портфеля. Примем за $latex Pi$ стоимость нового портфеля:
$latex Pi left(S_t,sigma,tauright)=frac{2}{T}left[frac{S_t-S_*}{S_*} - logfrac{S_t}{S_*}right]+frac{tau}{T}sigma^2$
(11)
Первое слагаемое в выплате по портфелю из формулы (11) описывает $latex 1/S_*$ форвардных контрактов на акцию с ценой поставки $latex S_t$. Это не опцион, это линейный актив, который может быть статически захеджирован, один раз и на весь период, без каких либо оценок волатильности акции. Второе слагаемое $latex -log left(S_t/S_*right)$ описывает короткую позицию по log-контракту с расчетной ценой $latex S_*$. Хеджирование данного контракта зависит от волатильности акции. Таким образом, чувствительность портфеля к волатильности базового актива полностью содержит в себе log-контракт.
Предположим, что динамику цен базового актива можно описать с помощью уравнения:
$latex frac{dS_t}{S_t}=muleft(t,dots right)dt + sigmaleft(t,dots right) dW_t$
(12)
Для упрощения предположим также, что дивиденды по акциям не начисляются.
Формула для дисперсии случайного процесса имеет вид:
$latex V=frac{1}{T}int^T_0{sigma^2left(t,dots right)dt}$
(13)
Процедура оценки свопа ничем не отличается от процедуры оценки любого другого производного инструмента. Стоимость форвардного контракта F на будущую реализованную волатильность со страйком K равна ожидаемой выплате в текущих ценах под риск нейтральной мерой:
$latex F=Eleft[e^{-rT}left(V-Kright)right]$
(14)
где
r — безрисковая ставка, соответствующая времени T;
E — математическое ожидание.
Справедливой стоимостью будущей реализованной дисперсии является страйк $latex K_{var}$, для которого текущая стоимость контракта равна нулю:
$latex K_{var}=Eleft[Vright]$
(15)
Используя формулы (13) и (15), получаем формулу для вычисления справедливой стоимости дисперсии:
$latex K_{var}=frac{1}{T}Eleft[int^T_0{sigma^2left(t,dots right)dt}right]$
(16)
Применив лемму Ито для $latex log S_t$, находим:
$latex dleft( log S_t right) = left( mu - frac{1}{2} sigma^2 right) dt + sigma dW_t$
(17)
Вычитая (17) из (12), получаем:
$latex frac{dS_t}{S_t}-dleft(log S_tright)=frac{1}{2} sigma^2 dt$
(18)
Просуммировав (18) от 0 до T, получаем:
$latex Vequivfrac{1}{T}int^T_0{sigma^2dt}=frac{2}{T}left[int^T_0{frac{dS_t}{S_t}}-logfrac{S_t}{S_0}right]$
(19)
Данное тождество определяет стратегию репликации дисперсии. Первое слагаемое в скобках соответствует финансовому результату от непрерывной ребалансировки позиции в акциях таким образом, что стоимость $latex 1/S_t$ акций в любой момент времени составляет $1. Второе слагаемое представляет собой статичную короткую позицию в контракте, выплата по которому на экспирацию составляет логарифм доходности акции за период.
Формула (19) предлагает метод вычисления справедливой стоимости дисперсии. При этом риск-нейтральное ожидаемое значение правой части формулы представляет собой стоимость репликации:
$latex K_{var}=frac{2}{T}Eleft[int^T_0{frac{dS_t}{S_t}}-logfrac{S_T}{S_0}right]$
(20)
Ожидаемое значение первого слагаемого в скобках в формуле (20) составляет стоимость ребалансировки портфеля, состоящего из $latex 1/S_t$ акций. В риск-нейтральном мире с постоянной безрисковой ставкой цена хеджирования такого портфеля составит:
$latex Eleft[int^T_0{frac{dS_t}{S_t}}right] = rT$
(21)
Второе слагаемое — это log-контракт. В виду того, что не существует подобного свободно торгующегося контракта, для воспроизведения выплат по нему необходимо выделить из его профиля выплат на экспирацию линейную и нелинейную части и реплицировать каждую отдельно. Линейную часть можно продублировать с помощью форвардного контракта на акцию со сроком T, оставшуюся нелинейную часть — с помощью ванильных опционов со сроком экспирации T.
Для определения границы между ликвидными put и call опционами введем параметр $latex S_*$, обозначающий эту границу. Выплату по log-контракту представим в виде:
$latex logfrac{S_T}{S_0}=logfrac{S_T}{S_*}+logfrac{S_*}{S_0}$
(22)
Второе слагаемое в правой части (22) — это константа, не зависящая от финальной цены акции $latex S_T$, следовательно, должно быть реплицировано только первое слагаемое. Как его повторить известно из формулы (8) — это форвардный контракт плюс портфель опционов с весами обратными квадрату величины страйка:
$latex -logfrac{S_T}{S_*}=-frac{S_T-S_*}{S_*}+int^{S_*}_0{frac{1}{K^2}left[K-S_Tright]^+dK}+int^{S_*}_0{frac{1}{K^2}left[S_T-Kright]^+dK}$
(23)
Справедливое значение будущей дисперсии может быть связано с начальным справедливым значением каждого слагаемого в формуле (21). Используя равенства (21) и (23), получаем:
$latex K_{var}=frac{2}{T}left(rT-left(frac{S_0}{S_*}e^{rT}-1right) - log frac{S_*}{S_0} + e^{rT}int^{S_*}_0{frac{1}{K^2}Pleft(Kright)dK}+e^{rT}int^{infty }_{S_*}{frac{1}{K^2}Cleft(Kright)dK}right)$
(24)
где P(K) и C(K) означают, соответственно, текущие справедливые цены put и call опционов со страйком K. Если используются текущие рыночные цены опционов, получается текущая рыночная оценка будущей дисперсии. Именно эта формула лежит в основе расчета индекса волатильности VIX.
Формула (4) —это дискретная копия формулы (24), из которой убраны первые три слагаемых (вероятно, для упрощения). Определенные интегралы представлены в виде соответствующих сумм. Последнее слагаемое в формуле (4) — это элемент корректировки в случаях, когда цена форварда F не совпадает с центральным страйком $latex K_0$.
Заключение
В основе расчета индекса волатильности российского рынка RVI лежит методика вычисления индекса волатильности VIX Чикагской биржи. Согласно данной методике значение индекса представляет собой взвешенное среднее волатильностей двух опционных серий. Данное усреднение предполагает, что в результате получится значение волатильности, соответствующее 30-дневному периоду. Методика расчета волатильности для каждой опционной серии, участвующей в расчетах VIX (и RVI), основывается на теории оценки свопов волатильности, подробно описанной в [3]. Моделирование справедливой стоимости свопа волатильности имеет ряд допущений, одно (и основное, по мнению автора) из них — это то, что динамика цен представляет собой геометрическое броуновское движение, т.е. непрерывный процесс без скачков (jumps). Это допущение может послужить причиной недооценки волатильности индексами VIX и RVI.
Список литературы
- Методика расчета Индекса волатильности российского рынка, Московская Биржа, 11.04.2014, fs.moex.com/files/6756
- The CBOE Volatility Index – VIX, the Chicago Board Options Exchange, September 22, 2003, www.cboe.com/micro/VIX/vixwhite.pdf
- More than you ever wanted to know about volatility swaps, Demeterfi K., Derman E., Kamal M. and Zou J., Goldman Sachs Quantitative Strategies Research Notes, March 1999
Автор: Олег Мубаракшин, Quant Lab
Посты и ссылки по теме:
- Инструментарий фондового рынка: что такое опционы, и как они работают
- Как стать квантом в HFT-компании
- How-to: как выбрать язык программирования для создания торгового робота
- Какие языки программирования наиболее востребованы в сфере финансов
- Аналитические материалы о фондовом рынке от экспертов ITinvest
Автор: itinvest