Есть такая интересная задача — построение 3D структуры по набору изображений (фотографий) — Structure from Motion. Как её можно решить? После некоторых размышлений приходит на ум такой алгоритм. Найдём на всех изображениях характерные особенности (точки), сопоставим их друг с другом и триангуляцией найдём их трёхмерные координаты. Тут правда есть проблема — неизвестно положение камер при съёмке. Можно ли их найти? Вроде можно. Действительно, пусть у нас N точек на кадре и M кадров. Тогда неизвестных будет 3 * N (трёхмерные координаты точек) + 6 * (M — 1) (координаты камер (вместо 6 может стоять другое число, но сути это не меняет)). Уравнений же у нас 2 * M * N (у каждой точки на каждом изображении есть две координаты). Выходит, что уже для двух изображений и 6 точек задачка разрешима. Под катом описание принципиальной схемы решения задачи SfM (по возможности без формул — но со ссылками для вдумчивого изучения).
План такой:
- Найти ключевые точки
- Найти соответствия между точками для последовательных пар изображений (хотя можно находить и для всех пар изображений)
- Отфильтровать ложные соответствия
- Решить систему уравнений и найти трёхмерную структуру вместе с положениями камер
План вроде простой и понятный. И, конечно, вся интрига в 3-м и 4-м пунктах.
1. Точки
Нахождение точек проблем не вызывает. Есть масса методов. Самый известный — SIFT. Он достаточно надёжно находит ключевые точки с учётом их масштаба и ориентации (что важно при произвольном движении камеры). Есть несколько open-source реализаций этого метода.
2. Соответствия
К каждой точке должно прилагаться её описание (дескриптор). Если дескрипторы точек на разных изображениях близки, то можно считать, что один и тот же физический объект. Простейший дескриптор — небольшая окрестность точки. Но в идеале, конечно, дескриптор должен быть независим от масштаба и ориентации изображения. В методе SIFT используется именно такой. Тогда поиск соответствий сводится к обходу всех ключевых точек одного изображения и поиску наиболее близкого дескриптора на другом изображении.
3. Фильтрация ложных соответствий
Ясно, что при любом качестве дескриптора ложных соответствий будет много. Их нужно отфильтровать. Здесь можно выделить два этапа:
- Независящая от геометрии фильтрация
- Фильтрация по эпиполярному ограничению
Независящая от геометрии фильтрация описана всё в том же методе SIFT. Там несколько простых фильтров, например: наилучшее соответствие из первого изображения во второе должно совпадать с наилучшим соответствием из второго в первое.
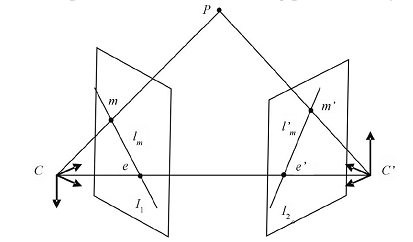
Эпиполярная геометрия. C и C' — оптические центры камер. Если точка P на первом изображении спроектирована в m. Тогда на другом изображении её проекцию нужно искать на прямой l'm.
Самая сильная фильтрация — это, конечно, с использованием эпиполярного ограничения. Её геометрический смысл в том, что для каждой точки одного изображения соответствующая ей точка на другом изображении находится на некоторой линии (которая не зависит от истинных трёхмерных координат точки). Математически это свойство выражается уравнением mTFm'=0. Здесь m=(u,v,1)T — однородные координаты ключевой точки на изображении, а F — фундаментальная матрица. Важнее всего тут то, что данное соотношение не зависит от трёхмерной структуры наблюдаемой сцены.
Поскольку фундаментальная матрица нам неизвестна, то для фильтрации ложных соответствий можно использовать следующий метод:
- Выберем случайно несколько точек и посчитаем по ним фундаментальную матрицу (метод вычисления описан в [1], раздел 14.3.2).
- Посчитаем, сколько ещё точек удовлетворяют условию mTFm'=0 с заданной точностью.
- Если количество точек достаточно велико, прекращаем цикл, иначе идём на пункт 1.
Этот нехитрый алгоритм называется RANSAC и идеально подходит для нашей задачи. И да — он таки достаточно хитрый и с ним тоже можно намучиться. Ну или можно использовать OpenCV.
4. Поиск трёхмерной структуры
Пора наконец выяснить, как же связаны точки в пространстве с точками на изображении. Тут всё просто — проективным преобразованием. По счастью, специфика моей задачи (наблюдение в телескоп с малым полем зрения) позволяла использовать аффинную геометрию камеры. Геометрические параметры камеры состоят из двух частей:
- Внешние параметры, определяющие положение камеры в пространстве (матрица поворота R 3х3 и вектор сдвига t 3х1).
- Внутренние параметры, определяющие проектирование изображения на ПЗС камеры. Сюда входят масштабирование по каждой из осей, угол между осями и коэффициенты искажения более высоких порядков. Для случая с квадратными пикселями и аффинной камерой остаётся только один параметр — масштаб k.
Уравнение наблюдения (связь между трёхмерными координатами (X, Y, Z)T точки и её положением на изображении (u, v)T) можно записать так:
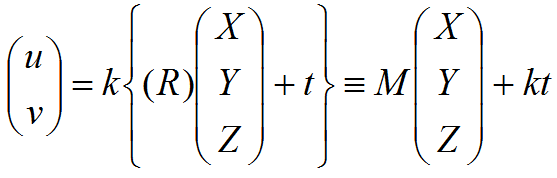
Здесь важно заметить, что в аффинной геометрии третья строка игнорируется, и от матриц поворота и сдвига можно использовать только две строки.
Получается, что нам нужно подобрать внешние (и внутренние) параметры всех камер и трёхмерные координаты точек так, чтобы это соотношение выполнялось как можно точнее для всех точек.
Есть два пути решения этой проблемы. Первый — попытаться решить эту нелинейную систему скопом нелинейными методами (bundle adjustment). Основная проблема тут очевидна — необходимо уметь решать очень большие системы нелинейных уравнений (ну а точнее — минимизировать нелинейную функцию в многомерном пространстве) и добиваться их сходимости к корректному решению. Другой путь —решить задачку по возможности аналитически. Так мы и поступим.
И тут нам на помощь проходит метод факторизации. Оказывается, используя сингулярное разложение можно решить задачу для аффинной камеры для случая, когда все точки видны со всех камер (на практике это означает «для каждой пары изображений отдельно»). Обоснование можно найти в [1], раздел 18.2.
- Сдвинем все точки на всех изображениях так, чтобы центр масс находился в начале координат. Это позволяет полностью исключить из уравнений вектор сдвига.
- Составим из проекция всех найденных точек матрицу наблюдения
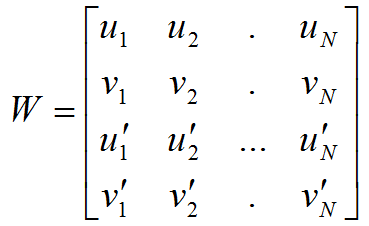. Тогда, записав все матрицы камер друг под другом в матрицу M, а все трёхмерные точки друг рядом с другом в матрицу X получаем уравнение W=MX. - Найдём сингулярное разложение W=UDVT. Тогда матрицы камер получаются из первых трёх столбцов U, перемноженных на сингулярные значения. Трёхмерная аффинная структура получается из первых трёх столбцов матрицы V .
Слишком просто? Да — тут есть подвох. Дело в том, что наше решение найдено с точностью до аффинного преобразования, т.к. мы проигнорировали структуру матрицы поворота (а она вовсе не произвольная). Чтобы поправить ситуацию нужно учесть, что камеры у нас описываются ортогональными матрицами, или просто заметив, что W=MX=MCCTX для любой ортогональной матрицы C (описание метода есть в [2], раздел 12.4.2.)
Матрица поворота должна удовлетворять следующим условиям:
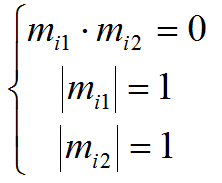
где mij – строки матрицы каждой камеры. Эти ограничения можно использовать для поиска матрицы C, приводящей аффинную структуру к евклидовой:
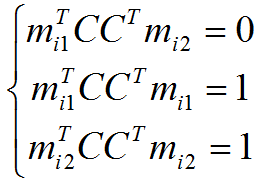
Эта система уравнений нелинейна относительно C, однако линейна относительно D=CCT. Из D матрица C получается взятием квадратного корня от матрицы. Домножив матрицы камер справа на C, а трёхмерную структуру слева на CT, получим корректную евклидову структуру, которая также удовлетворяет матрице наблюдения.
Ну и последнее — объединение трёхмерных структур от разных пар камер. Тут есть небольшой нюанс. Полученные нами положения камер центрированы относительно набора точек, а для разных пар камер набор точек разный. Так что нужно найти на двух парах камер пересекающийся набор точек. Тогда для пересчёта координат нужно лишь найти преобразование между этими наборами точек.
Вот мы и получили трёхмерную евклидову (т. е. с сохранением углов и отношений длин отрезков) структуру. На изображении в начале поста — такая структура для модели Энергия-Буран (одно из исходных изображений ниже). Такая структура называется разреженной (sparse), т.к. точек относительно немного. Получение из этого плотной (dense) структуры и натягивание текстур — совсем другая история.
Литература
- R. Hartley, A. Zisserman, “Multiple View Geometry in Computer Vision”
- Форсайт, Понс. «Компьютерное зрение. Современный подход»
Автор:
