Сегодня вслед за первыми квантовыми алгоритмами, которые мы уже рассмотрели (см. алгоритм Дойча и алгоритм Дойча-Йожи — если кто-то ещё не читал эти статьи, то предлагаю предварительно с ними ознакомиться, поскольку без этого изложение может показаться несколько туманным), предлагаю изучить алгоритм Гровера для неструктурируемого квантового поиска. Этот алгоритм был разработан американским математиком Ловом Гровером в 1996 году (уже намного позже того, как модель квантовых вычислений стала в моде). Этот алгоритм использует свойство квантовой интерференции для того, чтобы решать крайне насущную задачу по поиску значения некоторого параметра, на котором заданная функция выдаёт определённый результат.
Данный алгоритм не показывает экспоненциального выигрыша для задачи по сравнению с классической вычислительной моделью, однако для больших значений выигрыш (квадратичный) является существенным. Однако это общий алгоритм для решения довольно обобщённой задачи, и доказано, что лучшего результата в рамках модели квантовых вычислений добиться нельзя. В более частных алгоритмах это возможно.
Эта статья является продолжением в цикле статей по модели квантовых вычислений, поэтому если начать читать её без ознакомления с предыдущими статьями цикла, что-то может показаться непонятным. Так что читателя, который впервые набрёл на эти мои заметки, я отправляю к первым статьям: 1, 2, 3, 4.
Итак, если кто-то заинтересовался, то как обычно добро пожаловать под кат.
Полуформальное описание алгоритма
Задача формулируется следующим образом. Пусть есть бинарная функция от n бинарных же аргументов, которая принимает значение 1 только на одном из них (а на остальных 2n – 1 значениях, стало быть, принимает 0). Необходимо найти это значение входных аргументов, имея только функцию (для квантовых вычислений данную в виде оракула, как это полагается).
Естественно, что в классическом варианте в среднем необходимо просмотреть 2n/2 вариантов входных значений, поскольку в лучшем случае удастся найти «счастливый номер» с первой попытки, а в худшем потребуется перебрать все 2n вариантов. А вот алгоритм Гровера позволяет сделать это за π/4 √(2n) обращений к оракулу. Понятно, что при увеличении числа входных кубитов n разница в производительности становится кардинальной. Однако, как уже написано выше, суперполиномиального увеличения производительности здесь нет и не предвидится.
По своей сути это задача неструктурированного поиска. Если есть неупорядоченный набор данных («стог сена») и требуется найти в нём какой-то один элемент, удовлетворяющий специфическому требованию (этот элемент один такой — «иголка»), алгоритм Гровера поможет, поскольку альтернативой является классический перебор вариантов. Например, если рассмотреть аналогию с базой данных автомобилистов с именами, упорядоченными по алфавиту (и пусть в ней будет взаимно однозначное соответствие между фамилией и номером автомобиля), то упорядоченным поиском является поиск номера автомобиля по фамилии (делается, например, методом дихотомии, если нет индекса). А неупорядоченным поиском является обратная задача — поиск фамилии по номеру автомобиля. В данной аналогии оракулом является функция (преобразованная соответствующим образом), которая по фамилии возвращает номер автомобиля. Тогда эта задача сводится к задаче Гровера при помощи кодирования фамилий в бинарное представление, а сама функция возвращает ответ на вопрос «Владеет ли данный автомобилист N автомобилем X?», где N — входной параметр функции, а X — параметр алгоритма, как бы «зашиваемый» внутрь оракула при его построении. Соответственно, этот оракул возвращает значение 1 («да») только единственно для той фамилии, напротив которой в базе данных стоит искомый номер автомобиля.
Алгоритм Гровера состоит из следующих шагов:
- Инициализация начального состояния. Необходимо подготовить равновероятностную суперпозицию состояний всех входных кубитов. Это делается при помощи применения соответствующего гейта Адамара, который равен тензорному произведению n унарных гейтов Адамара друг на друга.
- Применение итерации Гровера. Данная итерация состоит из последовательного применения двух гейтов — оракула и так называемого гейта диффузии Гровера (оба будут детально рассмотрены ниже). Эта итерация осуществляется √(2n) раз.
- Измерение. После применения итерации Гровера достаточное количество раз необходимо измерить входной регистр кубитов. С очень высокой вероятностью измеренное значение даст указание на искомый параметр. Если необходимо увеличить достоверность ответа, то алгоритм прогоняется несколько раз и вычисляется совокупная вероятность правильного ответа.
Квантовая схема этого алгоритма, само собой разумеется, зависит от размера входных данных, поскольку от этого напрямую зависит количество применений итерации Гровера. В общем виде такая схема может быть изображена при помощи диаграммы, показанной на следующем рисунке.
Теперь обратим своё внимание на оракул и гейт диффузии, поскольку они являются сердцем алгоритма. Оракул в данном случае должен быть построен не совсем стандартным способом. Если вспомнить процесс преобразования классической бинарной функции в оракул, то можно понять, что принимая на вход два квантовых реестра (x, y), он должен выдавать на выходе пару (x, y ⊕ f(x)). Однако в случае алгоритма Гровера оракул должен инвертировать фазу у того квантового состояния, которое соответствует искомому значению x (напомним, что мы по заданному значению f(x) ищем x, то есть решаем обратную задачу). Это значит, что оракул должен на выходе выдавать значение (-1)f(x)|x>. Фазовый коэффициент (-1)f(x) установлен именно таким, поскольку f(x) = 1 тогда и только тогда, когда функция получает на вход искомое значение x, и именно в этом случае фазовый коэффициент становится равен -1. Другими словами, оракул Uw действует следующим образом:
- Uw
|w>= -|w> - Uw
|x>=|x>, x ≠ w
Гейт диффузии, в свою очередь, представляет собой соединение трёх гейтов, два из которых стандартны — это многокубитовые гейты Адамара. А вот между ними находится специальный гейт, который, по сути, осуществляет переворот кубитов относительно среднего значения. Его представление в виде аналитической формулы (2|0n><0n| — In) несколько затуманивает суть, поскольку его матричное представление просто — в верхнем левом углу матрицы стоит значение 1, в остальных позициях главной диагонали стоит значение -1, а в остальных местах стоят 0:
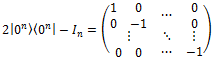
Но того же самого можно достичь, если в вышеприведённой формуле заменить |0n> на |+n>, и тогда не надо применять гейты Адамара до и после применения этого специального гейта. Так что оператор диффузии Гровера будет выглядеть как:
(2|+n><+n| — In)
Другими словами, с такой формой оператора диффузии квантовая схема алгоритма Гровера становится следующей:
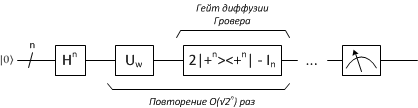
Программная реализация
Чтобы не быть голословным, можно рассмотреть этот алгоритм в его реализации на языке программирования Haskell. Для этого продолжим пользоваться тем набором функций, которые уже тянутся в этой серии публикаций из статьи в статью. Этот набор позволит «заглянуть» в недра алгоритма (чего не позволил бы, например, язык Quipper, поскольку предоставляет очень высокоуровневые средства генерации квантовых схем).
Но перед написанием кода нам опять надо немного заняться квантовой схемотехникой, поскольку надо спроектировать оракул в виде гейта. Для разнообразия (и укрепления навыков квантовой системотехники) можно рассмотреть функцию от трёх переменных, то есть оракул будет получать на вход 3 кубита (и, естественно, на выходе тоже будет 3 кубита). Рассмотрим такую задачу:
f(x1, x2, x3) = x1 & x2 & x3
Эта функция принимает значение 1 только на одном из восьми вариантов входных значений, что и требуется для алгоритма Гровера. Нет никакой разницы, какую именно из восьми возможных функций такого вида на трёх переменных рассматривать, но эта функция более проста с технической точки зрения. Как обычно для построения оракула можно воспользоваться таблицей.
| X1 | X2 | X3 | f(X) | (-1)f(X) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | -1 |
Этой таблице соответствует следующая матрица 8×8:
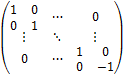
Поскольку мы сейчас начинаем реализацию более серьёзных вещей, чем рассматривались в предыдущих статьях, нам надо добавить некоторое количество полезных для конструирования оракулов, гейтов и прочего, служебных функций. В частности, необходимо добавить функцию, которая уже использоваласть в операторе тензорного произведения:
groups :: Int -> [a] -> [[a]]
groups i s | null s = []
| otherwise = let (h, t) = splitAt i s
in h : groups i t
Теперь перейдём к определению новых гейтов и операторов над ними. В соответствии с описанием алгоритма Гровера, нам потребуется оператор вычитания матриц друг из друга, а также функция для создания гейтов для нескольких кубитов на основе гейта для одного кубита. По крайней мере, эта функция потребуется для тензорного произведения гейтов I и H, чтобы иметь возможность применять их к квантовым регистрам, состоящим из нескольких кубитов.
Для начала определим простой оператор для получения разности матриц:
(<->) :: Num a => Matrix a -> Matrix a -> Matrix a
m1 <-> m2 = zipWith (zipWith (-)) m1 m2
Ну и для порядка определим такой же оператор для сложения матриц:
(<+>) :: Num a => Matrix a -> Matrix a -> Matrix a
m1 <+> m2 = zipWith (zipWith (+)) m1 m2
Здесь опять необходимо принять во внимание то, что разработчик сам должен следить за размерностью своих векторов и матриц.
Теперь перейдём к функциям для генерации гейтов. Пока были реализованы лишь функции для представления гейтов, обрабатывающих один или максимум два кубита. Однако при помощи оператора тензорного произведения и функции entangle можно создавать функции для представления гейтов, обрабатывающих произвольное количество кубитов. Например, вот так выглядит обобщённая функция, преобразующая заданный однокубитовый гейт в тот же гейт, обрабатывающий заданное количество кубитов:
gateN :: Matrix (Complex Double)
-> Int -> Matrix (Complex Double)
gateN g n = foldl1 (<++>) $ replicate n g
Очень просто и изящно. При помощи стандартной функции replicate создаётся список из заданного количества однокубитовых гейтов (при этом разработчик сам должен следить за тем, что сюда передаются именно однокубитовые гейты, хотя функция вполне будет работать и с многокубитовыми). Далее этот список сворачивается посредством оператора тензорного произведения (<++>). А вот так эта функция используется:
gateIn :: Int -> Matrix (Complex Double)
gateIn = gateN gateI
gateHn :: Int -> Matrix (Complex Double)
gateHn = gateN gateH
Как видно, первая функция формирует тождественное преобразование для заданного количества кубитов, а вторая — преобразование Адамара опять же для заданного количества кубитов. Эти два многокубитовых гейта очень важны в модели квантовых вычислений и часто используются во всевозможных квантовых схемах.
Наконец-то можно обратиться к реализации самого алгоритма Гровера. Начнём с оракула:
oracle :: Matrix (Complex Double)
oracle = matrixToComplex [[1, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, -1]]
Тут никакой сложности нет, необходимо просто закодировать матрицу. Конечно, вдумчивый читатель уже давно самостоятельно расширил представленный набор функций и определил функцию высшего порядка для генерации подобных оракулов (и многих иных). Но мы пока будем действовать по старинке.
Теперь реализуем функцию для представления оператора диффузии Гровера. С учётом тех соображений относительно смены базиса (использовать кубит в квантовом состоянии |+> вместо |0>), её определение будет крайне простым:
diffusion :: Matrix (Complex Double)
diffusion = 2 <*> (qubitPlus3 |><| qubitPlus3)
<-> gateIn 3
where
qubitPlus3 = toVector $
foldl1 entangle $
replicate 3 qubitPlus
Берём три кубита в состоянии |+> (qubitPlus), делаем из них список кубитов и сворачиваем его при помощи функции entangle. Далее переводим полученный квантовый регистр в векторное представление. Так получается локальное определение qubitPlus3.
Затем этот квантовый регистр qubitPlus3 векторно умножаем сам на себя, в результате чего получается матрица |+><+|, которая далее умножается на 2. Ну и из результата вычитается единичная матрица, подготовленная для трёх кубитов (то есть размера 8×8). При помощи реализованных ранее операторов написание таких функций становится делом очень приятным.
Что же, теперь осталось реализовать сам алгоритм Гровера. Вот определение функции для трёх кубитов:
grover :: Matrix (Complex Double) -> IO String
grover f = initial |> gateHn 3
|> f |> diffusion
|> f |> diffusion
>>> (measure . fromVector 3)
where
initial = toVector $
foldr entangle qubitZero $
replicate 2 qubitZero
В локальном образце initial опять готовится начальное состояние, которое, если присмотреться, равно |000>. Далее оно направляется в гейт Адамара для трёх кубитов, в результате чего получается равновероятностная суперпозиция из восьми квантовых состояний, которые могут быть на трёх кубитах. Затем два раза прогоняется цикл Гровера, поскольку 2 ≈ √23. После этого осуществляется измерение.
Что будет, если добавить в эту квантовую схему третий цикл Гровера? Всё просто — результаты станут хуже. Читателю предлагается самостоятельно подумать над ответом на вопрос «Почему?».
Поскольку алгоритм Гровера является вероятностным, он выдаёт правильный ответ только с какой-то очень высокой вероятностью. Это значит, что временами при запуске функции grover мы будем получать неправильный ответ, поэтому в данном случае предлагается оценить вероятность получения правильного ответа. Реализуем такую функцию:
main f n = do l <- replicateM n $ grover f
return $
map (length &&& head) $ group $ sort l
Она применяет алгоритм Гровера для заданного оракула заданное количество раз, а результатом её работы является гистограмма результатов алгоритма (то есть список пар вида (частота появления, результат)). Далее эта функция была запущена миллион раз, в результате чего был построен вот такой график:
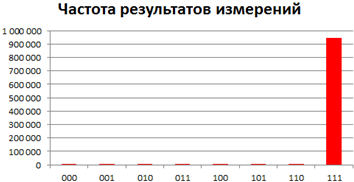
Правильный результат был получен примерно в 94.5 % случаев, а остальные результаты имеют частоту примерно в 0.78 %. Этого вполне достаточно для того, чтобы иметь возможность запустить алгоритм Гровера три раза и выбрать из этих трёх запусков результат, повторившийся по крайней мере дважды.
Вдумчивый читатель к этому времени уже должен был задаться вопросом, а что если оракул будет возвращать фазу -1 на нескольких входных данных, а не на одном? В этом случае алгоритм Гровера тоже работает, как это ни странно (хотя ничего странного в этом как раз и нет, если рассмотреть последовательность умножений матриц). Однако для нахождения одного правильного ответа из множества требуется намного меньше итераций.
Пусть l — количество значений входных параметров, на которых функция принимает значение 1 (то есть оракул возвращает фазу -1). Тогда для нахождения одного правильного значения с большой вероятностью требуется √2n/l) итераций Гровера. Это можно продемонстрировать следующим кодом:
oracle' :: Matrix (Complex Double)
oracle' = matrixToComplex [[1, 0, 0, 0, 0, 0, 0, 0],
[0, -1, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, -1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, -1]]
Если запустить функцию main с этим оракулом и дать возможность выполнить построение гистограммы на миллионе запусках, то будет явлена примерно следующая диаграмма:
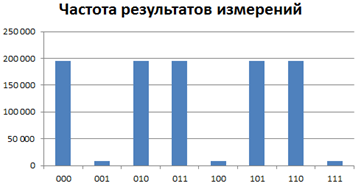
Что это? Правильные ответы получили наименьшую частоту? А всё правильно, поскольку сейчас функция grover, которая вызывается из функции main, выполняет две итерации Гровера, а для оракула с тремя правильными ответами необходима одна итерация. Как только выполнено больше итераций, чем требуется по алгоритму, ситуация переворачивается с ног на голову (поскольку у нас происходит переворот относительно среднего). Но в данном конкретном случае одной итерации так же недостаточно, поскольку частотные вероятности правильных и неправильных ответов будут достаточно близки друг к другу (это резонно, поскольку была сделана только одна итерация).
В общем, как показывает этот пример, разработчик при использовании алгоритма Гровера всегда должен внимательно следить за количеством итераций и не допускать переворота ситуации в противоположную сторону.
На этом описание алгоритма Гровера можно завершить. Теперь читателю вполне должно быть понятно, как он работает, какова математическая подоснова, и как можно реализовать этот алгоритм на языке программирования.
Заключение
Заинтересованного читателя как обычно можно отослать к исходному коду модуля. Также в комментариях приветствуется обсуждение как самого алгоритма, так и всей модели квантовых вычислений в общем. Ну а я в следующих публикациях постараюсь затронуть уже более интересные алгоритмы.
Мои предыдущие статьи по теме квантовых вычислений:
- Слово малое об обратимых вычислениях
- Реализация алгоритма Дойча на языке Haskell
- Квантовая схемотехника: некоторые приёмы и техники
- Разворачиваем язык квантового программирования Quipper
- Продолжаем изучать квантовые вычисления: алгоритм Дойча-Йожи
Автор: Darkus
