Одним вечером я наткнулся на статью о реализации одномерного клеточного автомата с помощью комонад, однако материал неполон и немного устарел, в связи с чем решил написать русскоязычную адаптацию (заодно рассмотрев двумерные клеточные автоматы на примере Game of Life)
Universe
Рассмотрим тип данных Universe, определенный следующим образом:
data Universe a = Universe [a] a [a]
Это бесконечный в обе стороны список, но с фокусом на неком элементе, который мы можем сдвигать с помощью функций:
left, right :: Universe a -> Universe a
left (Universe (a:as) x bs) = Universe as a (x:bs)
right (Universe as x (b:bs)) = Universe (x:as) b bs
По сути это тип-застежка (zipper), но мы можем рассматривать это как константный Си-указатель на бесконечную область памяти: к нему применимы операции инкремента, декремента. Но как его разыменовывать? Для этого определим функцию, достающую сфокусированное значение:
extract :: Universe a -> a
extract (Universe _ x _) = x
Например, Universe [-1, -2..] 0 [1, 2..] представляет из себя все целые числа. Тем не менее, Universe [0, -1..] 1 [2, 3..] это те же самые целые числа, но с немного измененным контекстом (мы указываем на другой элемент).

Если мы захотим получить все степени 2, то нам нужен способ применить функцию (2**) к Universe целых чисел. Достаточно несложно определить инстанс класса Functor, который подчиняется всем законам:
instance Functor Universe where
fmap f (Universe as x bs) = Universe (fmap f as) (f x) (fmap f bs)
-- соответственно
powersOf2 = fmap (2**) (Universe [-1, -2..] 0 [1, 2..])
-- ..0.25, 0.5, 1, 2, 4..
В клеточном автомате значения клеток зависят от значений всех остальных клеток на предыдущем шаге. Поэтому мы можем создать Universe всех сдвигов и правило их свертки:
duplicate :: Universe a -> Universe (Universe a)
duplicate u = Universe (tail $ iterate left u) u (tail $ iterate right u)

Правило свертки должно иметь тип Universe a -> a, таким образом для Universe Bool примером правила может послужить:
rule :: Universe Bool -> Bool
rule u = not (lx && cx && not rx || (lx==cx))
where lx = extract $ left u
rx = extract $ right u
cx = extract u
Применив правило к Universe всех сдвигов, мы получаем следующее состояние автомата:
next :: Universe a -> (Universe a -> a) -> Universe a
next u r = fmap r (duplicate u)
-- соответственно
un = Universe (repeat False) True (repeat False) `next` rule

Комонады
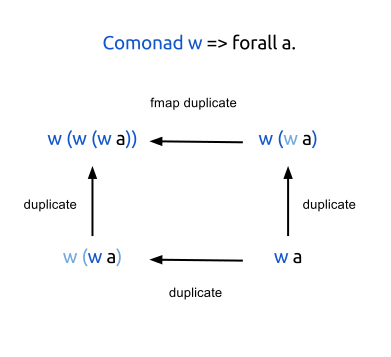
Мы можем заметить, что наши функции подчиняются следующим законам:
extract . duplicate = id
fmap extract . duplicate = id
duplicate . duplicate = fmap duplicate . duplicate
Поэтому, Universe образует комонаду, а функция next соотвствует оператору (=>>). Комонада — это дуал монады, в связи с чем можно проследить некие аналогии между их операциями. Например, join совмещает вложенные контексты, а duplicate — напротив, удваивает контекст; return помещает в контекст, а extract — извлекает из него, и т.д.
Двумерный клеточный автомат
Теперь, мы можем с тем же успехом реализовать двумерный клеточный автомат. Для начала объявим тип двумерного Universe:
newtype Universe2 a = Universe2 { getUniverse2 :: Universe (Universe a) }
В Haskell очень легко применять функцию ко вложенным контейнерам с помощью композиции fmap, поэтому написать инстанс класса Functor для Universe2 не составит никаких проблем:
instance Functor Universe2 where
fmap f = Universe2 . (fmap . fmap) f . getUniverse2
Инстанс комонады делается аналогично с обычным Universe, и поскольку Universe2 является лишь оберткой, мы можем определить методы в терминах уже имеющихся. Например, extract достаточно просто выполнить дважды. В duplicate, однако, мы должны получать сдвиги вложенных контекстов, для чего определятся вспомогательная функция
instance Comonad Universe2 where
extract = extract . extract . getUniverse2
duplicate = fmap Universe2 . Universe2 . shifted . shifted . getUniverse2
where shifted :: Universe (Universe a) -> Universe (Universe (Universe a))
shifted u = Universe (tail $ iterate (fmap left) u) u (tail $ iterate (fmap right) u)
Это почти все! Осталось только определить правило и применять его с помощью (=>>). В Game of Life новое состояние клетки зависит от состояния соседних клеток, так что определим функцию их нахождения:
nearest3 :: Universe a -> [a]
nearest3 u = fmap extract [left u, u, right u]
neighbours :: (Universe2 a) -> [a]
neighbours u =
[ nearest3 . extract . left
, pure . extract . left . extract
, pure . extract . right . extract
, nearest3 . extract . right
] >>= ($ getUniverse2 u)
А вот и само правило:
data Cell = Dead | Alive
deriving (Eq, Show)
rule :: Universe2 Cell -> Cell
rule u
| nc == 2 = extract u
| nc == 3 = Alive
| otherwise = Dead
where nc = length $ filter (==Alive) (neighbours u)
Остался лишь скучный вывод, который я не буду рассматривать отдельно.
Заключение
Таким образом, мы можем реализовать любой клеточный автомат, всего лишь определив функцию rule. Бесконечное поле мы получаем в подарок, благодаря ленивым вычислениям, хотя это и создает такую проблему, как линейное потребление памяти.
Дело в том, что поскольку мы применяем правило к каждому элементу бесконечного списка, то для вычисления клеток, к которым еще не было обращения, необходимо будет пройти все предыдущие шаги, а значит их нужно хранить в памяти.
Исходные коды обоих файлов:
module Universe where
import Control.Comonad
data Universe a = Universe [a] a [a]
newtype Universe2 a = Universe2 { getUniverse2 :: Universe (Universe a) }
left :: Universe a -> Universe a
left (Universe (a:as) x bs) = Universe as a (x:bs)
right :: Universe a -> Universe a
right (Universe as x (b:bs)) = Universe (x:as) b bs
makeUniverse fl fr x = Universe (tail $ iterate fl x) x (tail $ iterate fr x)
instance Functor Universe where
fmap f (Universe as x bs) = Universe (fmap f as) (f x) (fmap f bs)
instance Comonad Universe where
duplicate = makeUniverse left right
extract (Universe _ x _) = x
takeRange :: (Int, Int) -> Universe a -> [a]
takeRange (a, b) u = take (b-a+1) x
where Universe _ _ x
| a < 0 = iterate left u !! (-a+1)
| otherwise = iterate right u !! (a-1)
instance Functor Universe2 where
fmap f = Universe2 . (fmap . fmap) f . getUniverse2
instance Comonad Universe2 where
extract = extract . extract . getUniverse2
duplicate = fmap Universe2 . Universe2 . shifted . shifted . getUniverse2
where shifted :: Universe (Universe a) -> Universe (Universe (Universe a))
shifted = makeUniverse (fmap left) (fmap right)
takeRange2 :: (Int, Int) -> (Int, Int) -> Universe2 a -> [[a]]
takeRange2 (x0, y0) (x1, y1)
= takeRange (y0, y1)
. fmap (takeRange (x0, x1))
. getUniverse2
import Control.Comonad
import Control.Applicative
import System.Process (rawSystem)
import Universe
data Cell = Dead | Alive
deriving (Eq, Show)
nearest3 :: Universe a -> [a]
nearest3 u = fmap extract [left u, u, right u]
neighbours :: (Universe2 a) -> [a]
neighbours u =
[ nearest3 . extract . left
, pure . extract . left . extract
, pure . extract . right . extract
, nearest3 . extract . right
] >>= ($ getUniverse2 u)
rule :: Universe2 Cell -> Cell
rule u
| nc == 2 = extract u
| nc == 3 = Alive
| otherwise = Dead
where nc = length $ filter (==Alive) (neighbours u)
renderLife :: Universe2 Cell -> String
renderLife = unlines . map concat . map (map renderCell) . takeRange2 (-7, -7) (20, 20)
where renderCell Alive = "██"
renderCell Dead = " "
fromList :: a -> [a] -> Universe a
fromList d (x:xs) = Universe (repeat d) x (xs ++ repeat d)
fromList2 :: a -> [[a]] -> Universe2 a
fromList2 d = Universe2 . fromList ud . fmap (fromList d)
where ud = Universe (repeat d) d (repeat d)
cells = [ [ Dead, Alive, Dead]
, [Alive, Dead, Dead]
, [Alive, Alive, Alive] ]
main = do
gameLoop $ fromList2 Dead cells
gameLoop :: Universe2 Cell -> IO a
gameLoop u = do
getLine
rawSystem "clear" []
putStr $ renderLife u
gameLoop (u =>> rule)
Спасибо int_index за помощь в подготовке статьи!
Автор: x0m9k