Доклад Никиты Налютина на конференции SQA Days – 13, 26-27 апреля 2013 г. Санкт-Петербург, Россия
Анонс. Новые методики тест-дизайна не всегда рождались одномоментно, не все в инженерной практике может появиться в результате только лишь одного озарения и гениальных идей, увиденных во сне. Достаточно большая часть современных практик тестирования появилась в результате кропотливой теоретической и экспериментальной работы по адаптации математических моделей. И, хотя, для того, чтобы быть хорошим тестировщиком, вовсе не обязательно быть математиком, полезно понимать, какая теоретическая база лежит в основе того или иного метода тестирования. В докладе я расскажу о том, какую базу для тестирования дает математическая логика, теория формальных языков, математическая статистика и другие разделы математики; какие направления, связанные с тестированием, существуют в теоретическом computer science; появления каких новых методов можно ожидать в ближайшее время

Добрый день, уважаемые коллеги! Меня зовут Никита Налютин. Я надеюсь, у меня получится скрасить ваш послеобеденный сон небольшим докладом про математику в тестировании. Сначала я немного расскажу, кто я такой и как я пришел в тестирование.
В тестирование я пришел одиннадцать лет назад из разработки. Начинал как тестировщик-автоматизатор, занимался тестированием авиационного софта. Если вы летаете на самолетах Airbus, наверное, две или три системы, стоящие сегодня на их борту, проходили через мои руки. После этого работал в разных предметных областях: занимался тестированием трейдинговых систем в Deutsche Bank, немного поработал в замечательной компании Undev. Сейчас работаю в компании Experian, где я занимаюсь тест-менеджментом по России, странам СНГ и Европе. Кроме непосредственно тестирования за последние одиннадцать лет получилось сделать много разных интересных вещей. Преподаю в трех отечественных университетах. Не спрашивайте, как у меня это получается – сам не знаю. В 2007 году удалось выпустить книгу по верификации и тестированию, при поддержке компании Microsoft. Говорят, что получилось неплохо.

О чем сегодня пойдет речь? Зачем нам нужна математика в тестировании. Почему мы не можем тестировать без математики. В каких случаях такой вариант возможен, а в каких нет. На нескольких примерах посмотрим, как математику можно применять на практике. Как и куда стоит смотреть, когда мы начинаем тестировать что-то новое.

Поговорим о том, как и где можно учиться математике в приложении к тестированию. И немного поговорим о том, как можно уйти в науку, продолжая заниматься тестированием, стоит ли вообще это делать в наших практических реалиях, интересны ли кому-нибудь занятия наукой сейчас.

Зачем мы вообще поднимаем вопрос необходимости математики в тестировании. Вчера на одном из докладов я увидел поразивший меня слайд, смысл которого сводился к следующему. В качестве недостатка одной из систем указано то, что чтобы ей пользоваться, у тестировщика должно быть развито аналитическое . Мне всегда казалось, что аналитическое

На самом деле со времен М.В. Ломоносова в жизни изменилось не так много, как могло бы показаться. Ум в порядок приводить нужно всем, и тестировщикам в частности. Тестировщикам нужны и специальные инструменты. Аль-Капоне использовал револьвер и доброе слово, тестировщикам я бы предложил использовать математику и доброе слово. С помощью математики и доброго слова с разработчиками можно сделать много разных интересных вещей.
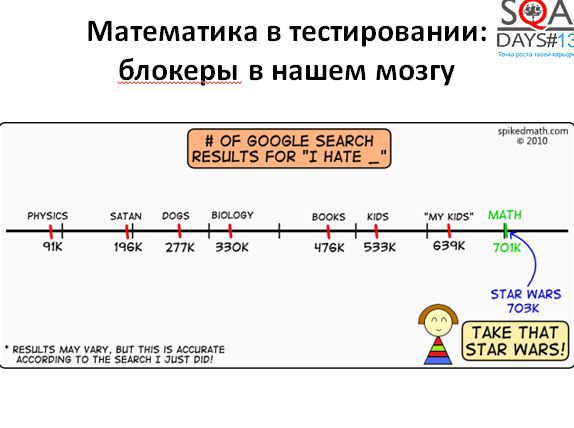
На самом деле интересный вопрос: почему мы не пользуемся математикой в нашей повседневной деятельности. Ответ прост – мы ее просто не любим. Простая статистика: возьмем запрос в Google “Я ненавижу …». И получим:
• 703 тысячи ответов: Я ненавижу «Звездные Войны»
• 701 тысяча ответов: я ненавижу математику
Математика уступает только Звездным Войнам! Неплохо, правда? Если эту ненависть несколько декомпозировать, то можно выделить три блокера, не дающие нам использовать математику.

Первый блокер – математика в тестировании это формальное доказательство правильности программ, которое плохо работает на практике. Эта область науки довольно хорошо развита и широко известна в узких кругах. Настолько широко, что сразу же приходит на ум многим тестировщикам, стоит с ними заговорить о математике в тестировании. Следующая мысль – «это слишком высокие материи, они не работают на практике». Так вот…
Математика – это не только формальная верификация. Мы можем тестировать, используя математические методы, не доказывая ничего, а просто пользоваться математикой, как инструментом.
Второй блокер — для того, чтобы математические методы работали, необходимо составление подробных спецификаций. Тоже далеко не так. Вас никто не заставляет писать подробную спецификацию и доказывать, что программа работает правильно. Вам не требуется подробной математической модели всей системы, с которой работаете. Можно пользоваться математикой, как небольшим удобным инструментом.
Достаточно идей в голове и небольшого упорядочивания этих идей, т.е. аналитических способностей.
И самым известный блокер, это мысль о том, что
математика — это что-то очень сложное
Это неправда. Я своими глазами видел факультатив по математической логике для учащихся 5-го класса, ребята сидели и решали довольно сложные логические задачи. А вы, тестировщики, хуже пятиклассников? Мне кажется, что нет.
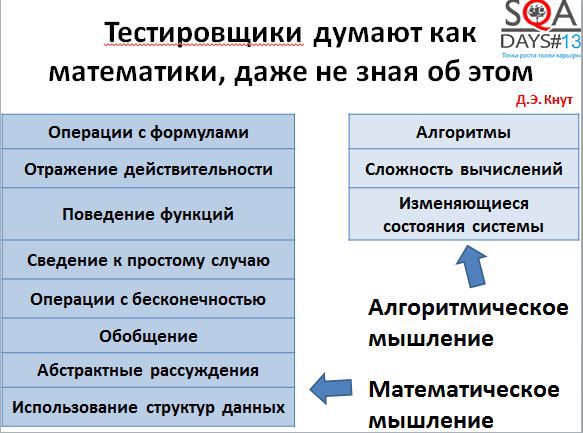
Если попробовать разобраться в том, как думают математики, то результат будет довольно интересным. Всем известный Дональд Кнут в свое время написал статью «Algorithmic Thinking and Mathematical Thinking» (http://www.jstor.org/discover/10.2307/2322871?uid=3738936&uid=2&uid=4&sid=21103388081621). В ней он выделил несколько типов
Все эти типы
• отражение действительности
В самом деле, вы своими тестами отражаете действительность, показывая, насколько правильно работает система.
• сведение к простому случаю
Все мы пытаемся писать тесты, чтобы они были максимально простыми и, при этом, отсутствовала необходимость их переусложнять.
• обобщение
Мы пытаемся описывать тесты так, чтобы их можно было переиспользовать. Мы стараемся сначала написать шаблон для теста, а потом уже множество конкретных тестов по шаблону.
• абстрактные рассуждения
Все мы строим некоторую абстрактную модель системы у себя в голове, а потом тестируем ее.
• изменяющееся состояние системы
Как минимум, у нас есть два состояния системы: все работает или все сломано. Обычно таких состояний несколько больше, и в ходе тестирования мы изменяем состояние системы.
Если эта таблица вас не убедила, можно посмотреть на результаты исследования И.Я. Каплуновича (Каплунович И.Я. Содержание мыслительных операций в структуре пространственного

И.Я. Каплунович считает, что от нашего рождения и до момента математической грамотности, т.е. до момента, когда наши аналитические способности уже хорошо развины, проходит пять стадий. Начинаем с топологического уровня, где наши неупорядоченные мысли начинают укладываться в некоторую структуру. Двигаемся дальше, на четвертом уровне начинаем измерять, на пятом – оптимизировать.
Вам ничего это не напоминает? Правильно – пять уровней CMMI: первый уровень – только собрались, управляем. Второй-третий – добиваемся повторяемости и управляемости, четвертый – измеряем, пятый – оптимизируем. В самом деле похоже.

Если немного отвлечься от высоких материй, то можно сказать, что все идеи, которые выдвигают математики и хорошие инженеры – все они, по большому счету, созданы ленью.
Нам лень тратить много времени и долго решать задачи, поэтому мы садимся и придумываем что-нибудь интересное, быстро решаем задачу и начинаем заниматься другими задачами. Инженеры редко любят подход «Долго, дорого, скучно», математики тоже. В тест-дизайне лень отлично работает – мы можем лениться долго и со вкусом, а главное – результативно.
Давайте попробуем разобраться на нескольких примерах, кто, как и где может применять математику в тест-дизайне.

Начнем с самой очевидной области, с математической логики. С того как мы можем применять матлогику, чтобы оптимизировать покрытие кода нашей системы, не забывая при этом о том, что мы любим лениться. Вот небольшой пример: обычный «if» с двумя ветвями и длинная формула в условии.

Мой преподаватель по геометрии в десятом классе называл длинные-длинные формулы «крокодилами». Вот такой крокодил встретился у нас в коде. Для того чтобы покрыть обе ветви кода, нужно разобраться в структуре формулы, нужно разобраться, какие значения принимают переменные х1, х2, х3, х4. Можно, но как-то очень не хочется. Возникает вопрос: что мы можем сделать? Можно лениться непродуктивно и, забыв матлогику, протестировать этот код полным переобором. Получится 16 тестов. «Долго, дорого, скучно». Ну и просто не хочется.
Пытаемся уменьшить количество тестов – применяем MC/DC (11-12 тестов), решаем, что нам хватит покрытия по ветвям – получаем два теста…
А дальше – внезапно вспоминаем булеву алгебру. После преобразования исходного выражения получаем, что на значение истинности влияет только переменная x3. В результате мы получаем не только простой способ сгенерировать тесты (в однои x3 = true, в другом x3 = false), но и получаем повод пообщаться с разработчиком. Ведь это довольно странно, когда в коде есть довольно сложное логическое выражение, а на деле оно зависит только от одной переменной, возможно здесь где-то ошибка.

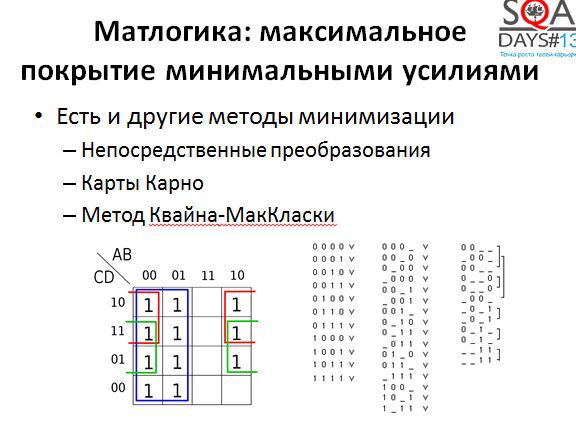
Вообще говоря, упрощать логические выражения можно и другими методами. Есть как минимум три метода, знакомые всем младшекурсникам технических специальностей. Непосредственные преобразования с использованием законов булевой алгебры работают всегда, карты Карно хороши когда в выражении мало переменных, а метод Квайна-МакКласки хорош даже для большого количества переменных и отлично алгоритмизуется. Если поискать, то можно найти даже методы минимизации выражений, учитывающие особенности предметной области, то есть опирающиеся не только на матлогику.
Попробуем разобрать следующий вопрос – состояние системы и тестирование изменяющихся состояний. Обычно состояний значительно больше, чем просто «работает» и «не работает», я несколько слукавил в начале выступления.
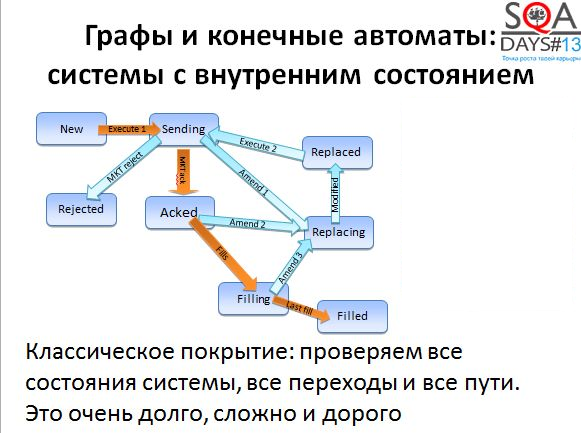
Например, ниже вы видите часть состояний, которые проходит биржевой ордер – заявка на покупку или продажу акций. Для того, чтобы сделка совершилась, заявка должна пройти несколько состояний. Сначала заявка создана, затем она подтверждается биржей, затем совершается множество мелких сделок на покупку и в конце-концов покупается или продается необходимое количество акций. Все состояния биржевого ордера отражаются в торговых системах, все переходы и состояния нужно проверять. На самом деле все несколько сложнее, но сейчас это не важно.
Обычно проверяются либо все состояния, либо все переходы, либо и то и другое вместе. Полное покрытие достижимо, но традиционно – «Долго, дорого, скучно». Попробуем облегчить себе жизнь и немного полениться. Как?
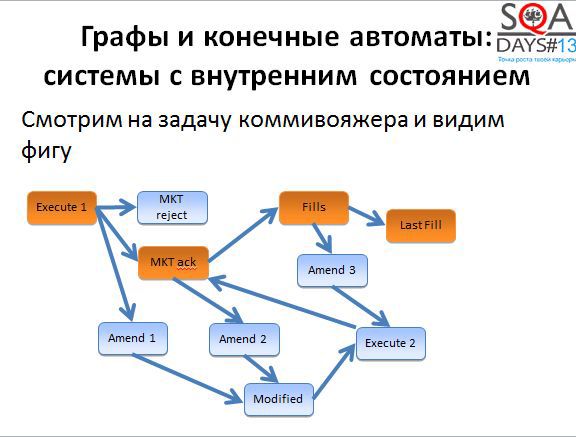
Вы наверняка слышали о задаче коммивояжера – задаче оптимизации на графах. Есть связанный с этой задачей алгоритм де Бройна.
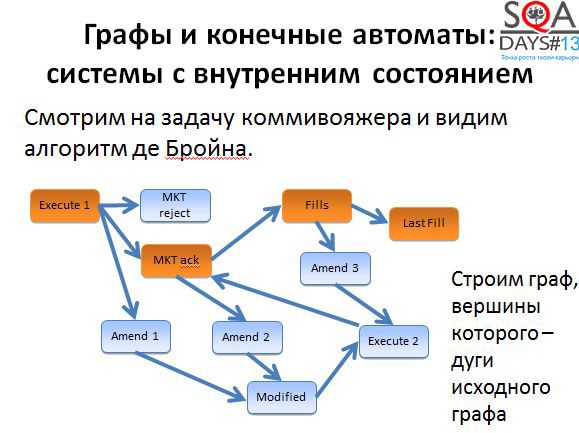
Нам не обязательно использовать алгоритм буквально, достаточно понимать, что он позволяет получить оптимальный или достаточно оптимальный набор коротких путей, которые мы можем пройти в графе для того, чтобы покрыть его полностью. Для того, чтобы алгоритм начал работать, нужно немного поработать нам. Сначала берем исходные состояния и строим граф новый граф, в котором вершины соответствуют переходам исходного графа. А дальше начинаем покрывать вершины нового графа (т.е. переходы старого).
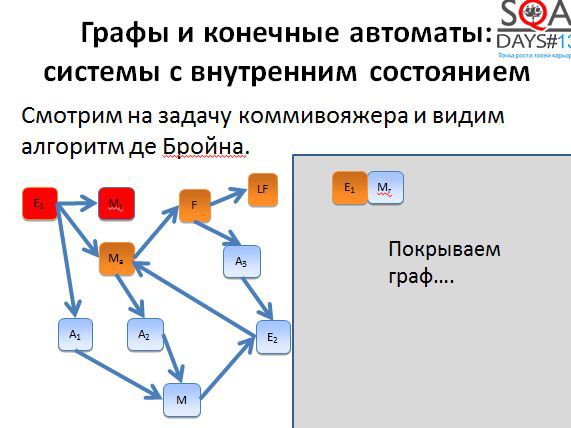
Первые два пути достаточно короткие. Начинаем строить третий путь и получаем очень-очень длинный.
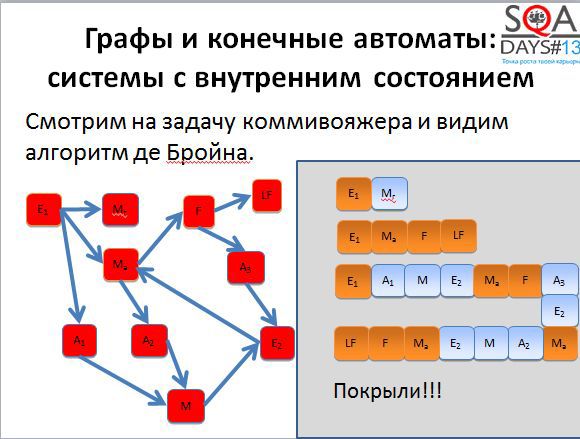
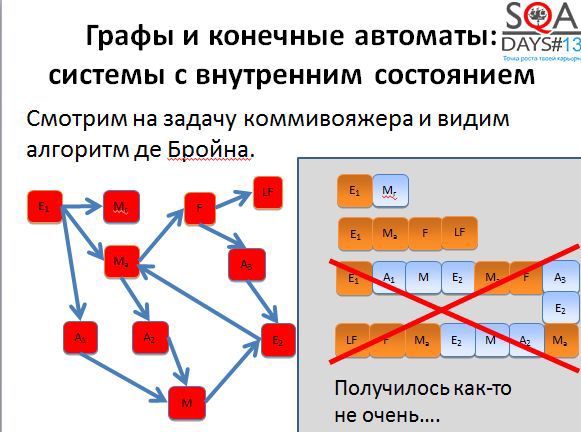
А теперь представим такую ситуацию. У вас есть три тестировщика. Первый выполняет первый тест, второй – второй тест, третий – третий тест. Первые двое заканчивают работу очень быстро, а вот последний сидит очень долго. А если это автотесты? Третий тест очень долго работает, результаты вы получается с большой задержкой.
Если применить алгоритм де Бройна, можно разрезать третью последовательность на несколько более коротких и хорошо распараллелить выполнение. Мы получаем пять тестов вместо трех, но при условии их параллельного выполнения, тестирование завершается намного быстрее.
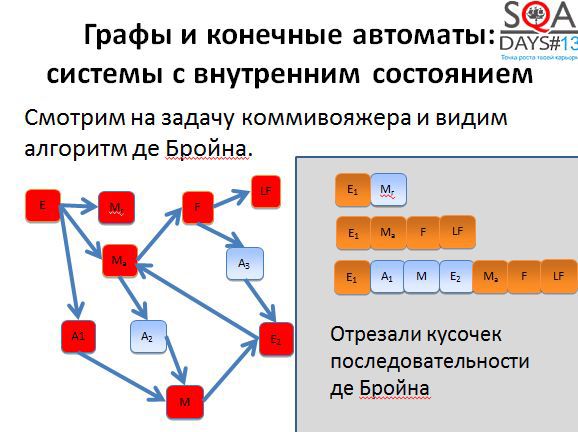
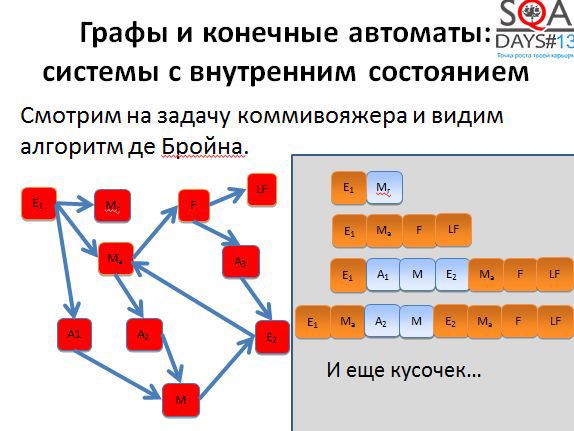


Кроме того, при появлении большего количества тестов появляется больше гибкости. Мы можем выполнять все тесты, а можем выкинуть мало интересные, можем расставить более высокие приоритеты тем тестам, которые проходят через наиболее интересные для нас состояния. Способов воспользоваться результатами алгоритма довольно-таки много. Причем обратите внимание, что алгоритм никак не использует специфичных для предметной области вещей, он работает с чисто абстрактными состояниями и переходами. А если попробовать придумать свой алгоритм, но с предметной областью и музами?


Третий пример. Есть базовое понятие в тестировании – класс эквивалентности. Казалось бы, что можно здесь придумать нового?

В каком классе эквивалентности должен быть минимум один тест. Плюс нужно проверять границы классов. Все это хорошо работает, если вы знаете классы эквивалентности и знаете граничные значения. А может получиться так, что классы явно не заданы и границы размыты. Может, например, сложиться так, что классы эквивалентности образуются вследствие работы системы на определенном специфическом оборудовании и никак не определены в требованиях к программному обеспечению.

Вполне реальный пример. Есть система, которая сохраняет в базу данных строки от 0 до 5 Мб длиной. В требованиях записано, что время на сохранение этой строки должно быть примерно одинаковым. Классический подход к тестированию дает нам три теста: пустая строка, строка 5 Мб и средняя строка в 2.5 Мб. Проверили, время сохранения одинаковое и укладывается в допустимую погрешность. Все хорошо.

Поставили в эксплуатацию, начали собирать реальные данные и обнаружили, что короткие строки сохранаются намного быстрее длинных. Начинаем экспериментировать, ничего не зная о причинах такого поведения, в результате получаем следующую картину.

Оказывается, кроме указанных критических точек есть еще две: 256 Б и 32 Кб. Почему? Поговорили с разработчиком, и получили в ответ рассказ про то, какую классную оптимизацию разработчик сделал: строки до 256 байт сохраняются как строки, до 32К как бинарные объекты в базу, а свыше 32к – в виде файлов на файловой системе. «Все равно у вас таких строк мало, а базе так легче». Такие классы эквивалентности искать намного сложнее и нам на помощь может прийти анализ результатов с промышленной среды или со среды приемочного тестирования. Если грамотно подойти к анализу этих данных, то мы сможем найти аномальные зоны.

Если применить теорию измерений, то можно сделать поиск аномальных зон более упорядоченным. Для получения базового предстваления можно воспользоваться хотя бы определениями из ГОСТ Р 50779. Термины, определенные в этом ГОСТе, можно использовать в качестве отправных точек для дальнейших поисков в спецлитературе и извлечь из теории измерений именно те знания, которые нужны именно вам.
Попробуем получить полезную информацию об аномалиях в нашем случае. Есть интервал с известными граничными значениями (минимум, максимум, середина). Есть некоторая неточная информация о том, что мы можем считать аномальной зоной. Строим функцию распределения вероятности того, что данное значение вызовет проблемы – например, что строка указанной длины будет сохраняться долго. Для примера возьмем нормальное распределение. Узкий и острый купол означает высокую уверенность в том, что эта зона аномальная, широкий купол означает низкую уверенность, например, в силу того, что у нас мало данных по этим значениям. Дальше начинаем применять выборочное тестирование и генерировать строки разной длины, «пристреливаясь». Там где купол более узкий «стреляем» тестами более кучно, там где более широкий – более широко, пытаясь нащупать более точную закономерность.

На скриншоте, представленном выше, видно: синим – мы угадали аномальную зону, там строки сохраняются медленно, красным – немножко не угадали – левее красной зоны нет никаких аномальных значений времени сохранения строк. Дальше модифицируем правое распределение и «пристреливаемся» еще раз.

Вторая пристрелка показала, что мы нашли аномальную зону более точно. И мы можем добавить к нашим исходным трем граничным значениям еще шесть – для каждой из двух аномальных областей.

Таким образом мы получили новые классы эквивалентности, которые не были видны заранее, но которые выведены из эксперимента, и которые могут быть использованы для тестирования поведения новых версий системы. Может быть наш разработчик придумает новую оптимизацию для хранения строк.

Еще один пример. Все знают, что такое pair-waise тестирование. Если кто не знает, то по этому методу есть куча литературы, а в двух словах он сводится к тому, что вместо того, чтобы тестировать все возможные сочетания входных параметров (что весьма долго), тестовые наборы формируются так, чтобы каждое значение параметра хотя бы один раз сочеталось с каждым значением остальных тестируемых параметров – это дает значительно меньшее количество тестов, и это хорошо работающий метод.

Но работает этот метод не всегда. Пусть наша система становится все сложнее и сложнее…

Сложнее и сложнее….

И становится сложной настолько, что начинает нравиться фанатам «Теории большого взрыва».

Хватит ли нам pair-wise для того чтобы хорошо оттестировать сложную систему с большим количеством входных параметров? Этот вопрос интересовал многих ученых и даже американский Национальный институт стандартов и технологий (NIST).

Под эгидой NIST существует проект ACTS, в рамках которого ведутся исследования в области комбинаторного тестирования. Согласно их исследованиям, pair-wise находит ошибки в 65-97% случаев. Если мы начинаем комбинировать не пары параметров, а тройки или четверки, т.е. использовать k-way тестирование, то мы получаем большее количество тестов, но и вылавливаем больше ошибок.

Используя знания о том, что на pair-wise свет клином не сошелся, мы можем выбрать устраивающий нас уровень покрытия и устраивающее нас количество тестов.
Здесь нам опять приходит на помощь математика, и мы можем воспользоваться результатами труда исследователей в проекте NIST ACTS.

Основа для pair-wise – это ортогональные матрицы, содержащие n-ки (пары, тройки, четверки, …) значений одинаковое количество раз.

Вместо ортогональных матриц в NIST предлагают использовать покрывающие матрицы (http://math.nist.gov/coveringarrays/coveringarray.html). Такие матрицы отличаются от ортогональных тем, что каждый набор значений встречается хотя бы один раз, а не «одинаковое количество раз». В данном случае тестов получается чуть меньше, в покрывающих матрицах могут образовываться некорректные тест-кейсы, но в целом само тестирование проходит значительно быстрее. На сайте NIST ACTS можно даже найти генераторы покрывающих матриц и уже рассчитанные матрицы для заданного количества входов и количеств их значений. Таким образом мы снова упрощаем себе жизнь при помощи математики, разобравшись один раз в комбинаторном тестировании и продолжая лениться.

При использовании покрывающих матриц можно уйти от pair-wise к k-way, не сильно увеличивая количество тестов.
Таким образом, мы поговорили о совсем небольшом наборе математических методов, которые можно сравнительно легко использовать при тестировании. В некоторые из них можно даже не погружаться очень глубоко.

На этом заканчивается та часть выступления, которая предназначена для инженеров по тестированию. Но тестирование на этом не кончается, есть еще и тест-менеджмент. Есть там и своя математика.

В тест-менеджменте очень много разных областей и везде можно найти нужные и полезные математические методы. Есть даже несколько ярких представителей российского IT-сообщества, всячески продвигающих математику.

Поэтому здесь я бросаю будущих тест-менеджеров-математиков и призываю их не лениться искать информацию, а лениться делать то, без чего можно обойтись.
Теперь я хочу поговорить о том, где тестированию можно учиться.

Дабы не уподобляться герою с картинки, стоит все же иногда впитывать те знания, которые вам дают в университете. Далеко не все из них – ненужный хлам, есть там и что-то полезное. Запоминайте хотя бы названия, потом почитаете, когда понадобится. Ну и не забывайте приводить ум в порядок – структурированное сознание – превыше всего.

Структура знаний в области Software Engineering – достаточно хорошо проработанная тема. Например, в США существует две крупных организации. Одна из них – это ACM, Association for Computing Machinery. Она занимается публикациями результатов исследований в области Computer Science и Software Engineering, организует интересные конференции, так или иначе связанные с теоретическим IT, является учредителем премии Тьюринга – аналогом Нобелевской премии для IT-исследований.
Помимо всего прочего, ACM публикует т.н. Curricula – высокоуровневые учебные планы, которые содержат информацию о том, чему надо учить студентов IT-специальностей, и что они должны знать на выходе из университета. Так, на слайде приведен набор математических дисциплин, необходимых для хорошего IT-специалиста. Обратите внимание на то, что там присутствует математическая экономика. Со временем вы, как тестировщики, начнете задумываться и об экономической составляющей тестирования – сколько оно стоит, что выгоднее – тестировать или нет. Здесь вам придут на помощь остаточные (или не остаточные) университетские знания.

Вторая крупная организация, которая выдает рекомендации, что должен знать выпускник – IEEE – Institute of Electrical and Electronics Engineers. Они публикуют Своды знаний (Body of Knowledge), в том числе Software Engineering Body of Knowledge, третья версия которого на момент доклада была в состоянии беты. В этом документе выпускнику университета рекомендуется уже несколько больший набор математических дисциплин.

Образование в области тестирования не ограничивается университетами. Можно обучаться и самому. Например, подготовиться к сдаче сертификационных экзаменов Quality Assurance Institute – там чуть больше базовых и теоретических вещей, чем в экзаменах ISTQB. Можно (и нужно) следить за международными конференциями по тестированию. Например, на конференции ICST очень хорошее сочетание теоретических и практических докладов. Есть www.arxiv.org – здесь всегда можно найти свежие статьи в самых разных областях, в числе и относящиеся к исследованиям в области тестирования. На scholar.google.com тоже всегда можно найти что-то интересное. Учиться можно и нужно всегда, главное постепенно учиться искать нужную информацию.

Если учиться (а может быть даже и учить) понравилось, то можно подумать и над тем, чтобы сделать исследования своим основным занятием.

Для этого в первую очерень надо ответить на вопрос «зачем?”. Ответ на этот вопрос у всех разный, но отвечать на него нужно, чтобы не потерять интерес к исследованиям.
Уходя в науку, вы обычно выбираете себе направление исследований, то, что вас заботит больше всего. Для меня в свое время любимой темой стало управление конфигурациями и методы оценки состояния разработки программных систем. Ваша любимая тема может быть совсем иной. Но если вы еще не знаете чем заниматься – посмотрите, про что пишут коллеги. В науке тоже есть своя мода – мода на исследования. Так, например, в конце 2012 года на одной из американских конференций были назаны наиболее популярные темы для исследований, приведенные на слайде ниже.


Таким образом путь в науку довольно прост – решаетесь, определяесь со своим «Зачем?», берете любое из актуальных направлений и начинаете пахать.
Если вы еще студент – делаете курсовую или диплом (не тяп-ляп, а всерьез, с отдачей).
Если вы хотите написать кандидатскую – готовьтесь потратить от двух до пяти лет на написание своей работы и апробацию ее на практике (семь кругов бюрократического ада за полгода до защиты – совершенно бесплатно).
Если вы уже кандидат или доктор наук – попробуйте поработать с зарубежными коллегами, поищите интересные постдоки.

Интересные исследования ведутся и в России, несколько фамилий приведены на слайде выше, я тоже пока не потерял интереса к исследованиям.
Ниже приведены ссылки, где можно посмотреть документы, на которые я ссылался.

Отдельное спасибо хочу сказать создателям Футурамы и Теории большого взрыва, как за иллюстрации, так и за возможность наблюдать за героями в течение нескольких лет.

На этом мой доклад завершен, я готов ответить на ваши вопросы.
Вопрос.
Ты говорил про купола: узкий и широкий. Получается, мы просто ищем точки для класса эквивалентности, используя статистику от реального использования системы. При этом мы никак не используем требования, а опираемся на конкретную релизацию системы. А потом меняются разработчики, пишут чуть иначе и мы начинаем поиск аномалий заново. Почему мы ищем эти точки постфактум, а не можем придумать как их искать заранее?
Ответ.
Анализ требований не дает нам полной гарантии тогло, что мы найдем все ошибки. Когда мы начинаем анализировать данные от работающей системы, то мы знаем о системе только то, что напимано в требованиях. А дальше мы пытаемся найти аномалии в поведении системы и упорядочить наши знания о ней. Аномалии все равно будут, требования все равно будут неполны, поэтому все что мы можем здесь сделать – искать аномалии более упорядоченно. Если исходной информации и нашей интуиции не хватит – мы ничего не найдем, но если нам есть на что опираться и удалось придумать способ анализа данных – мы можем найти ошибки, которые никогда бы не нашли, анализируя требования. Например, при помощи «куполов» и «пристрелки» мы как-то проверяли систему на показатели нагрузки. Она падала не только при пиковой нагрузке, но и при вполне средних показателях, задачей было найти – почему так происходит.
Вопрос.
А откуда вы взяли эти точки, когда тестировали нагрузку?
Ответ.
Была статистика проблем с производительностью из данных реальной эксплуатаци, плюс были некоторые экспертные оценки того, на каких параметрах система может начать падать.
Вопрос.
Есть ли у тебя какая-то статистика по тому, где и насколько широко применяются в компаниях те методы, о которых ты рассказал?
Ответ.
Вопрос очень хороший и я буду рад, если подобной статистикой поделиться аудитория. У меня нет подробной статистики по использованию, но я могу сказать, что все методы, о которых я рассказывал, применялись мной или моими коллегами на практике. Все они были созданы благодаря практическим потребностям для решения конкретных задач.
Вопрос.
У вас был слайд о диаграммах состояний системы. У вас были состояния, которые вы условно назвали плохими и, используя эти новые состояния, возможно придется все полностью переписать или нет?
Ответ.
Здесь все зависит от того, как мы пользуемся алгоритмом. В самом крайнем случае мы можем ничего не знать, о том, какая логика стоит за переходами между состояниями. В этом случае длинная цепочка переходов будет разрезана алгоритмом на несколько коротких, часть из которых может оказаться бессмысленной. Именно поэтому те цепочки переходов, которые получены после разрезания, нужно оценить на разумность и выбрать именно те, которые важны для тестирования. Бессмысленные (но возможные) пути изменения состояний системы могут привести нас к пониманию, что нужно часть системы переписать.
Вопрос.
Насколько эффективны методы, о которых вы рассказывали, для создания модели оптимальной нагрузки при нагрузочном тестировании? Можно ли создавать профиль нагрузки по имеющейся статистике?
Ответ.
В докладе речь шла немного о другом. Мы не искали оптимум, а только лишь искали аномалии в поведении системы. Когда этот метод применялся на практике для поиска аномалий при небольшой нагрузке, мы знали, что наша система хорошо ведет себя при большом потоке данных, приемлемо ведет себя при маленьком, но какой-то средний поток данных всегда вызывал проблему. Мы не искали оптимума, а искали конкретные проблемы способом, который позволял нам найти их чуть быстрее, чем просто перебором.
Автор: Polazhenko





