Этот цикл статей описывает волновую модель , серьезно отличающуюся от традиционных моделей. Настоятельно рекомендую тем, кто только присоединился, начинать чтение с первой части.
Наиболее просты для понимания и моделирования нейронные сети, в которых информация последовательно распространяется от слоя к слою. Подав сигнал на вход, можно так же последовательно рассчитать состояние каждого из слоев. Эти состояния можно трактовать как набор описаний входного сигнала. Пока не изменится входной сигнал, останется неизменным и его описание.
Более сложная ситуация возникает, если ввести в нейронную сеть обратные связи. Чтобы рассчитать состояние такой сети, уже недостаточно одного прохода. Как только мы изменим состояние сети в соответствии с входным сигналом, обратные связи изменят входную картину, что потребует нового пересчета состояния всей сети, и так далее.
Идеология рекуррентной сети зависит от того, как соотносится задержка обратной связи и интервал смены образов. Если задержка много меньше интервала смены, то нас, скорее всего, интересуют только конечные равновесные состояния, и промежуточные итерации стоит воспринимать, как исключительно расчетную процедуру. Если же они сопоставимы, то на первый план выходит именно динамика сети.
Ф. Розенблатт описал многослойные персептроны с перекрестными связями и показал, что они могут быть использованы для моделирования избирательного внимания и воспроизведения последовательности реакций (Rosenblatt, Principles of Neurodynamic: Perceptrons and the Theory of Brain Mechanisms, 1962).
В 1982 году Джон Хопфилд предложил конструкцию нейронной сети с обратными связями такую, что ее состояние может быть определено, исходя из расчета минимума функционала энергии (Hopfield, 1982). Оказалось, что сети Хопфилда обладают замечательным свойством – они могут использоваться как память, адресуемая по содержанию.
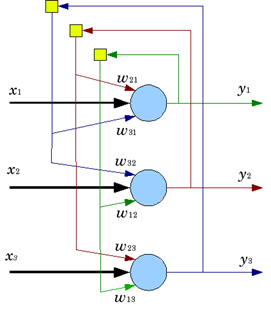
Сеть Хопфилда
Сигналы в сети Хопфилда принимают спиновые значения {-1,1}. Обучение сети – это запоминание нескольких образов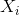 
. Запоминание происходит за счет настройки весов так, чтобы:
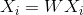
Что приводит к алгоритму, который простым неитерационным расчетом позволяет определить параметры сети:
где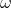 
– матрица, составленная из весов нейронов, а 
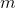– количество запоминаемых образов. Диагональ матрицы 
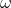полагается нулевой, что означает отсутствие влияния нейронов на самих себя. Веса, заданные таким образом, определяют устойчивые состояния сети, соответствующие запомненным векторам.
Функция активации нейронов имеет вид:
Входной образ присваивается сети, как начальное приближение. Затем начинается итерационная процедура, которая, если повезет, сходится к устойчивому состоянию. Таким устойчивым состоянием, скорее всего, будет один из запомненных образов. Причем это будет образ, наиболее похожий на входной сигнал. Другими словами, образ ассоциативно с ним связанный.
Можно ввести понятие энергии сети, как:
где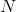 
– количество используемых нейронов. Каждому запомненному образу в таком случае будет соответствовать локальный энергетический минимум.
Хотя сети Хопфилда и очень просты, они иллюстрирует три фундаментальных свойства . Первое – это существование в динамике, когда любые внешние или внутренние возмущения заставляют покинуть состояние текущего локального минимума энергии и перейти к динамическому поиску нового. Второе – это способность прийти к квазиустойчивому состоянию, определяемому предыдущей памятью. Третье – ассоциативность переходов, когда в смене описательных состояний постоянно прослеживается определенная обобщенная близость.
Как и сети Хопфилда, наша модель изначально динамична. Она не может существовать в статичном состоянии. Любая волна существует только в движении. Вызванная активность нейронов запускает волны идентификаторов. Эти волны вызывают активность паттернов, узнавших знакомые волновые сочетания. Паттерны запускают новые волны. И так без остановки.
Но динамика наших сетей принципиально отличается от динамики сетей Хопфилда. В традиционных сетях динамика сводится к итерационной процедуре схождения состояния сети к устойчивому состоянию. У нас же динамика сродни тем процессам, что протекают в алгоритмических компьютерах.
Волновое распространение информации – это механизм передачи данных. Динамика этой передачи – это не динамика итерационного схождения, а динамика пространственного распространения идентификационной волны. Каждый цикл распространения информационной волны меняет картину вызванной активности нейронов. Переход коры в новое состояние означает смену текущего описания и соответственно смену картины нашей мысли. Динамика этих изменений опять же не является некой итерационной процедурой, а формирует последовательность образов нашего восприятия и .
Наша волновая модель значительно сложнее, чем простая динамическая сеть. Позже мы опишем достаточно много небанальных механизмов, регулирующих ее работу. Не удивительно, что и представление об ассоциативности в нашем случае оказывается сложнее, чем ассоциативность в сетях Хопфилда, и скорее напоминает концепции, свойственные компьютерным моделям представления данных.
В программировании под ассоциативностью понимается способность системы искать данные, похожие на образец. Например, если мы обращаемся к базе данных, указывая критерии запроса, то, по сути, мы хотим получить все элементы, похожие на образец, описываемый этим запросом.
На компьютере решить задачу ассоциативного поиска можно простым перебором с проверкой всех данных на соответствие критериям поиска. Но полный перебор трудоемок, гораздо быстрее поиск осуществляется, если данные заранее подготовлены так, что позволяют быстро формировать выборки, удовлетворяющие определенным критериям. Например, поиск в адресной книге можно значительно ускорить, если создать оглавление по первой букве.
Подготовленная должным образом память называется ассоциативной. Практическая реализация ассоциативности может использовать таблицы индексов, хэш-адресацию, бинарные деревья и тому подобные инструменты.
Независимо от реализации, ассоциативный поиск требует задания критериев похожести или близости. Как мы уже говорили, основные виды близости – это близость по описанию, близость по совместному проявлению и близость по общему явлению. Первая говорит о похожести по форме, остальные о сходстве по некой сути. Это напоминает поиск товара в Интернет-магазине. Если вы введете название, то получите список товаров, названия которых будут близки к заданному. Но кроме этого вы, скорее всего, получите еще один список, который будет называться, что-то вроде: «те, кто ищут этот товар, часто обращают внимание на…». При этом элементы второго списка могут по своим описаниям никак не походить на описание, сформулированное исходным запросом.
Посмотрим, как рассуждения об ассоциативности применимы к понятиям, используемым в нашей модели. Понятие у нас – это набор паттернов нейронов-детекторов, настроенных на один и тот же образ. Очень похоже, что одному паттерну соответствует отдельная кортикальная миниколонка. Образ – это определенное сочетание сигналов на рецептивном поле нейронов. На сенсорных зонах коры образ может быть сформирован сигналами топографической проекции. На более высоких уровнях образ – это узор активности, возникающий вокруг нейрона, при прохождении мимо него волны идентификаторов.
Для перехода нейрона в состояние вызванной активности требуется чтобы образ достаточно точно совпал с картиной весов на его синапсах. Так если нейрон настроен на детектирование определенного сочетания понятий, то волновой идентификатор должен содержать существенную часть идентификаторов каждого из них.
Срабатывание нейрона, когда повторяется большая часть понятий, составляющих его характерный стимул, называется узнаванием. Узнавание и связанная с ним вызванная активность не дают обобщенной ассоциативности. В таком режиме нейрон не реагирует ни на понятия, имеющие временную близость, ни на понятия, хотя и входящие в описание характерного для нейрона стимула, но встретившиеся отдельно от остального описания.
Нейроны, которые мы используем в нашей модели, и которые мы сравниваем с реальными нейронами , способны хранить информацию не только за счет изменения синаптических весов, но и благодаря изменениям в метаботропных рецептивных кластерах. За счет последних нейроны способны запоминать фрагменты картин окружающей активности. Повторение такой запомненной картины не ведет к появлению вызванной активности нейрона, состоящей из серии импульсов, а вызывает единичный спайк. Запомнит или нет нейрон что-либо таким образом определяется рядом факторов один из которых — изменение мембранного потенциала этого нейрона. Увеличение мембранного потенциала вызывает расхождение расщепленных концов метаботропных рецепторов, что заставляет их обрести необходимую для запоминания чувствительность.
Когда нейрон узнает характерный образ и переходит в состояние вызванной активности, его мембранный потенциал существенно повышается, что дает ему возможность запоминать на внесинаптической части мембраны окружающие его картины активности.
Можно предположить, что в момент вызванной активности нейрон запоминает все окружающие его волновые узоры. Такая операция имеет вполне определенный смысл. Предположим, что мы имеем полное описание происходящего, складывающееся из большого числа понятий. Часть из них позволит нейрону узнать то понятие, детектором которого является его паттерн (миниколонка). Узнавание обеспечит этому понятию участие в общем описании. При этом на нейронах, ответственных за само понятие зафиксируется, какие еще понятия входили в полную описательную картину.
Эта фиксация произойдет на всех нейронах, составляющих наш детекторный паттерн (миниколонку). Регулярное повторение такой процедуры приведет к накоплению на поверхности нейронов-детекторов рецептивных кластеров, чувствительных к определенным сочетаниям идентификаторов.
Можно предположить, что чем чаще какое-либо понятие будет встречаться совместно с активностью детекторного паттерна, тем выше будет вероятность того, что его самостоятельное появление будет определяться внесинаптическими рецепторами и вызывать единичный спайк. То есть если между понятиями присутствует совместность в проявлении, то нейроны одного понятия будут реагировать одиночным спайком, когда в волновом описании будет появляться другое ассоциативно связанное с ним понятие.
Одновременный одиночный спайк нейронов одного детекторного паттерна – это основание для запуска соответствующей идентификационной волны. Получается, что задав одно понятие и распространив его волновой идентификатор можно получить в волновом описании набор понятий, ассоциативно с ним связанных. Это можно сопоставить с тем, как база данных по запросу выдает список всех записей, попадающих под критерии этого запроса. Получив список от базы данных, мы используем дополнительные алгоритмы, чтобы продолжить работу с этим списком. Аналогично можно представить и работу . Получение доступа к ассоциациям – это только один из этапов его работы. На активность нейронов можно наложить дополнительные ограничения, которые позволят только части ассоциаций пробиться в волновое описание. Суть этих дополнительных ограничений во многом и определяет информационные процедуры, свойственные .
Предыдущие части:
Часть 1. Нейрон
Часть 2. Факторы
Часть 3. Персептрон, сверточные сети
Часть 4. Фоновая активность
Часть 5. Волны мозга
Часть 6. Система проекций
Часть 7. Интерфейс человек-компьютер
Часть 8. Выделение факторов в волновых сетях
Часть 9. Паттерны нейронов-детекторов. Обратная проекция
Часть 10. Пространственная самоорганизация
Алексей Редозубов (2014)
Автор: AlexeyR
