Коды Рида-Соломона относятся к недвоичным, блочным, помехоустойчивым кодам и могут использоваться в области хранения информации для избегания потери поврежденной информации.
На хабре есть пост посвященный кодированию информации кодами Рида-Соломона, но для примера автор использует простое поле Галуа. В данной статье описывается работа с расширенными полями Галуа, в частности GF(2^m), которые рационально использовать для цифровой информации. С моей аналогичной реализацией кодирования, декодирования, исправления ошибки можно ознакомится здесь.
При работе с кодами Рида-Соломона процент избыточных символов в 2 раза больше восстанавливаемого объема данных. Объясню на примере: если мы имеем последовательность из 10 символов и хотим иметь возможность восстановить ошибки в 3-ех из них (30% исходной информации), то нам нужно хранить 10+3*2=16 символов. Назовем каждую переменную: n – 10, количество информационных символов; f – 3, количество восстанавливаемых символов; g – 16, длина закодированной последовательности. Таким образом, формулу можно записать так: g = n + f * 2.
Поля Галуа
Для работы с информацией при кодировании и декодировании данных все арифметические операции выполняются в полях Галуа. Применяется так называемая полиномиальная арифметика или арифметика полей Галуа. Таким образом, результат любой операции также является элементом данного поля. Конкретное поле Галуа состоит из фиксированного диапазона чисел. Характеристикой поля называют некоторое простое число p. Порядок поля, т.е. количество его элементов, является некоторой натуральной степенью характеристики pm, где m∈N. При m=1 поле называется простым. В случаях, когда m>1, для образования поля необходим еще порождающий полином степени m, такое поле называется расширенным. GF(p^m) – обозначение поля Галуа.
Для работы с цифровыми данными естественно использовать p=2 в качестве характеристики поля. При m=1 элементом кодовой последовательности будет бит, при m=8 – 8 бит, то есть байт. Собственно коды Рида-Соломона работающие с байтами и являются наиболее распространенными.
Перед тем как переходить к операциям кодирования и декодирования разберемся с арифметикой полей Галуа на примере GF(2^3). Данное поле состоит из чисел от 0 до 7.
Операция сложения
Самой простой является операция сложения, которая является простым побитовым сложение по модулю 2 (ХОР).
Пример: 5+3=110=6
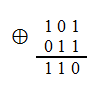
Операция умножения
К сожалению, операция умножения гораздо сложнее, чтобы ее осуществить, необходимо преобразовать числа в полиномиальную форму.
Пример: 5=101=1∙x^2+0∙x^1+1∙x^0=x^2+1
Как можно заметить число в полиномиальной форме представляет собой многочлен, коэффициентами которого являются значения разрядов в двоичном представлении числа.
Перемножим два числа в полиномиальной форме:
5∙7=(x^2+1)∙(x^2+x+1)=x^4+x^3+x^2+x^2+x+1=x^4+x^3+x+1=11011=27
Итак, во-первых, следует заметить, что даже в полиномиальной форме осуществляется сложение по модулю 2, поэтому x^2+x^2=0. Во-вторых, результат умножения 27 не входит в используемое поле GF(23) (оно же состоит из чисел от 0 до 7, как было сказано выше). Чтобы бороться с этой проблемой, необходимо использовать порождающий полином. Порождающий полином является неприводимым, то есть простым (по аналогии с простыми числами делится без остатка на 1 и на самого себя). В арифметике полей Галуа неприводимым полиномом является аналог простых чисел. Используем для примера порождающий полином f(x)=x^3+x+1.
Также предполагается, что x удовлетворяет уравнению f(x)=x^3+x+1=0
Вернемся к примеру с умножением:

Такой же результат можно получить как остаток от деления полинома, полученного при умножении на порождающий полином:
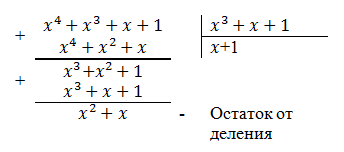
Составим таблицу умножения:
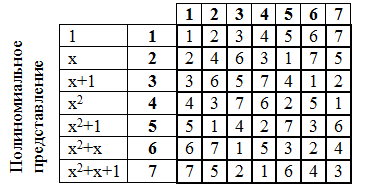
Операция деления
Операцию деления в полиномиальной форме понять, возможно, но достаточно тяжело. Поэтому гораздо лучше осуществлять его по таблице умножения.
Пример:6÷5=7
Большое значение имеет таблица степеней элементов поля Галуа. Возведение в степень также осуществляется в полиномиальной форме, аналогично умножению.
Пример:5^2=〖(x^2+1)〗^2=x^4+x^2+x^2+1=x^4+x^2+x+x^2+x+1=x∙(x^3+x+1)=x^2+x+1=111=7
Таким образом, составим таблицу степеней:

Таблица степеней обладает цикличностью: седьмая степень соответствует нулевой, значит восьмая соответствует первой и т.д. При желании можно это проверить.
В полях Галуа существует понятие примитивного члена – элемент поля, чьи степени содержать все ненулевые элементы поля. Просмотрев таблицу степеней видно, что этому условию соответствуют все элементы (ну кроме 1 естественно). Однако это выполняется не всегда, для примера приведу таблицу степеней для GF(16).
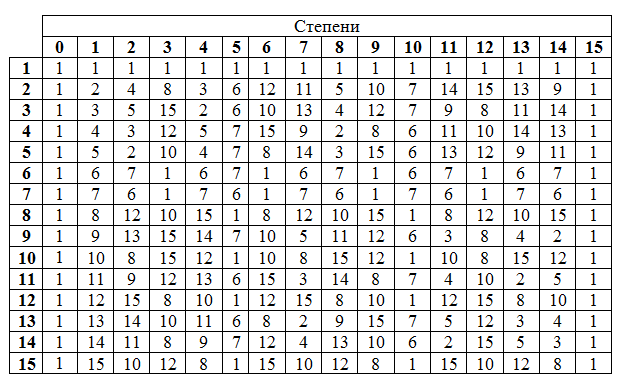
Для полей, которые мы рассматриваем, то есть с характеристикой 2, в качестве примитивного члена всегда выбирают 2. Учитывая его свойство, любой элемент поля можно выразить через степень примитивного члена.
Пример: 5=26, 7=25
Воспользовавшись этим свойством, и учитывая цикличность таблицы степеней, попробуем снова перемножить числа:
5∙7=2^6∙2^5=2^(6+5)=2^11=2^(11 mod 7)=2^4=6
Результат совпал с тем, что мы вычислили раньше.
А теперь выполним деление:
6÷5=2^4÷2^6=2^(4-6)=2^(-2)=2^((-2)mod 7)=2^5=7
Полученный результат тоже соответствует действительности.
Ну и для полноты картины посмотрим на возведение в степень:
5^2=(〖2^6)〗^2=2^(6∙2)=2^12=2^(12 mod 7)=2^5=7
Опять неожиданно получился такой же результат.
Такой подход к умножению и делению гораздо проще, чем реальные операции с использование полиномов, и для них нет необходимости хранить большую таблицу умножения, а достаточно лишь строки степеней примитивного члена поля.
Автор: coolweb